
- •Модуль 2. Аналитическая геометрия на плоскости и пространстве. Понятие функции
- •Тема 1. Прямая на плоскости
- •Тема 2. Кривые второго порядка
- •Тема 3. Уравнение плоскости
- •Тема 4. Взаимное расположение прямой и плоскости
- •Тема 5. Функция. Область определения
- •Тема 6. Непрерывность функции. Предел функции
Тема 5. Функция. Область определения
Определить область определения следующих функций:
1)
![]() ;
6)
;
6)
![]() ;
;
2)
![]() ;
7)
;
7)
![]() ;
;
3)
![]() ;
8)
;
8)
![]() ;
;
4)
![]() ;
9)
;
9)
![]() ;
;
5)
![]() ; 10)
; 10)
![]() ,
,
![]() .
.
Определить область определения и множество значений следующих функций:
1)
![]() ;
3)
;
3)
![]()
2)
![]() ;
4)
;
4)
![]() .
.
Записать функцию, выражающую зависимость радиуса r цилиндра от его высоты h при данном объеме V=1. Построить график этой функции.
Выразить площадь равнобокой трапеции с основаниями a и b как функцию угла при основании a. Построить график функции при a=2, b=1.
Исследовать на монотонность следующие функции:
1)
![]() ;
2)
;
2)
![]() 3)
3)
![]() ;
;
4)
![]() ;
5)
;
5)
![]() ,
,
![]() .
.
Определить, какие из данных функций
 являются четными, а какие нечетными:
являются четными, а какие нечетными:
1)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ,
;
4)
,
;
4)![]() ;
;
5)
![]() .
.
Используя правила преобразования графиков функций по графику функции
 ,
построить эскизы графиков следующих
функций:
,
построить эскизы графиков следующих
функций:
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() ;
;
4)
![]() ; 5)
; 5)
![]() ; 6)
; 6)
![]() ;
;
7)
![]() ; 8)
; 8)
![]() ; 9)
; 9)![]() ;
;
10)
![]() ; 11)
; 11)
![]() ; 12)
; 12)
![]() ;
;
13)
![]() ; 14)
; 14)
![]() ; 15)
; 15)
![]() ;
;
16)
![]() ; 17)
; 17)
![]() ;
19)
;
19)
![]() ;
;
20)
![]() ; 21)
; 21)
![]() ;
;
Построить эскизы графиков следующих функций:
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() ;
;
4)
![]() ; 5)
; 5)
![]() ; 6)
; 6)
![]() .
.
Тема 6. Непрерывность функции. Предел функции
Покажите, что функция
 ограничена в интервале
ограничена в интервале
 .
.Покажите, что функция
 не ограничена в любой окрестности
точки
не ограничена в любой окрестности
точки
 ,
однако не является бесконечно большой
при
,
однако не является бесконечно большой
при
 .
.С помощью
 рассуждений докажите, что:
рассуждений докажите, что:
1)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ; 4)
; 4)
![]() .
.
Пусть
 При таком выборе числа а
функция
При таком выборе числа а
функция
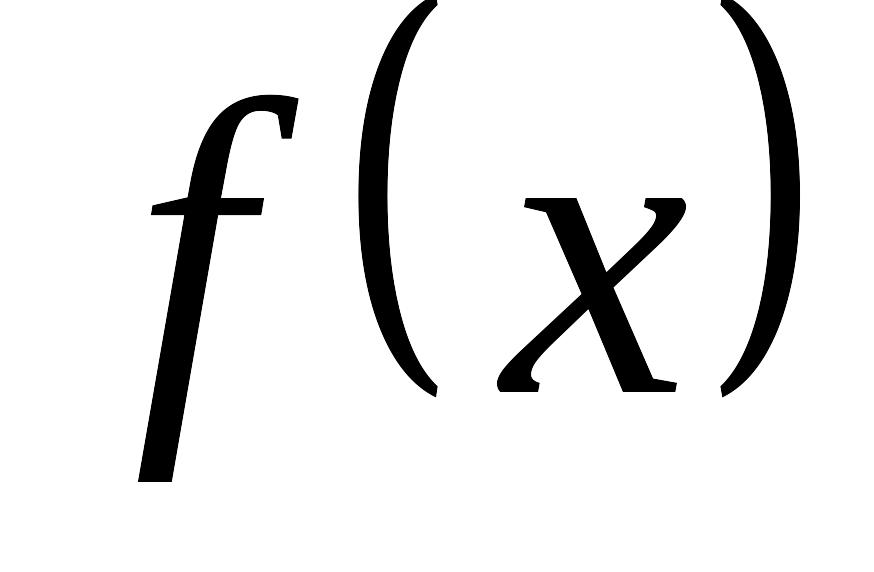 будет непрерывной? Построить ее график.
будет непрерывной? Построить ее график.С помощью рассуждений доказать, что функция
 непрерывна при
непрерывна при
 .
.Вычислите пределы:
1)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ; 4)
; 4)
![]() ;
;
5)
![]() ; 7)
; 7)
![]() ;
;
8)
![]() ; 9)
; 9)
![]() ;
;
11)
![]() ; 12)
; 12)
![]() ;
;
16)
![]() ; 17)
; 17)
![]() ;
;
18)
![]() ; 19)
; 19)
![]() ;
20)
;
20)
![]() ; 21)
; 21)
![]() ;
22)
;
22)
![]() ,
,
![]() ; 23)
; 23)
![]() ;
24)
;
24)
![]() ; 25)
; 25)
![]() ;
26)
;
26)
![]() ; 27)
; 27)
![]() ;
;
28)
![]() ; 29)
; 29)
![]() ;
;
30)
![]() ; 31)
; 31)
![]() ;
;
33)
![]() ;
34)
;
34)
![]() ;
;
35)
![]() ;
36)
;
36)
![]() ;
;
37)
![]() ; 38)
; 38)
![]() ;
;
39)
![]() ; 40)
; 40)
![]() ;
;
41)
![]() ; 42)
; 42)
![]() ;
;
44)
 ;
45)
;
45)
 ;
;
46)
![]() ; 47)
; 47)
![]() ;
;
48)
 ;
49)
;
49)
![]() ;
;
50)
![]() ; 51)
; 51)
![]() ;
;
52)
![]() ; 53)
; 53)
![]() ;
;
54)
![]() ; 55)
; 55)
![]() ;
;
56)
![]() ; 57)
; 57)
![]() ;
;
58)
![]() ;
59)
;
59)
![]() ;
;
60)
![]() ; 61)
; 61)
![]() ;
;
62)
![]() ; 63)
; 63)
![]() ;
;
64)
![]() ; 65)
; 65)
![]() ;
66)
;
66)
![]() ,
; 67)
,
; 67)
![]() ;
68)
;
68)
![]() ; 69)
; 69)
![]() ;
70)
;
70)
![]() ; 71)
; 71)
![]() ;
72)
;
72)
![]() ; 73)
; 73)
![]() ;
74)
;
74)
![]() ; 75)
; 75)
![]() .
.
Пусть дана функция
 .
Показать, что для каждого
.
Показать, что для каждого
 можно подобрать
можно подобрать
 такое, что
такое, что
 ,
если только
,
если только
 ,
а для
,
а для
 для всех значений х
этого сделать нельзя. В каких точках
нарушается непрерывность этой функции?
для всех значений х
этого сделать нельзя. В каких точках
нарушается непрерывность этой функции?С помощью рассуждений доказать непрерывность следующих функций:
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() ; 4)
; 4)
![]() ;
5)
;
5)
![]() ;
6)
;
6)
![]() ;
7)
;
7)
![]() ;
8)
;
8)
![]() .
.
Исследовать на непрерывность и изобразить графически следующие функции:
1)
![]() ,
если
,
если
![]() и
и
![]() – произвольно;
– произвольно;
2)
![]() ,
если
,
если
![]() и
и
![]() ;
;
3)
![]() ,
если
и
;
,
если
и
;
4)
![]() ,
если
и
,
если
и
![]() – произвольно;
– произвольно;
5)
![]() ,
если
и
,
если
и
![]() ;
;
6)
![]() ,
если
и
;
,
если
и
;
7)
 ,
если
,
если
![]() и
и
![]() – произвольно;
– произвольно;
8)
 ;
;
9)
![]() ,
если
и
,
если
и
![]() ;
;
1 0)
0)
![]() ;
;
11)
![]() .
.
Определить точки разрыва функций и исследовать характер этих точек если:
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() ;
4)
;
4)
 ; 5)
; 5)
![]() ; 6)
; 6)
![]() ;
7)
;
7)
![]() ; 8)
; 8)
![]() ; 9)
; 9)
![]() ;
10)
;
10)
![]() ; 11)
; 11)
![]() ; 12)
; 12)
 .
.
Пусть
 При каком выборе числа а функция
будет непрерывной?
При каком выборе числа а функция
будет непрерывной?Исследовать следующие функции на непрерывность и выяснить характер точек разрыва, если:
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]() 5)
5)
![]()
Показать, что при любом выборе числа функция
 будет разрывная при х=1.
будет разрывная при х=1.Функция теряет смысл при х=0. Определить число так, чтобы была непрерывна при х=0, если:
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() ;
4)
;
4)
![]() ; 5)
; 5)
![]() ; 6)
; 6)
![]() .
.
