
- •Модуль 2. Аналитическая геометрия на плоскости и пространстве. Понятие функции
- •Тема 1. Прямая на плоскости
- •Тема 2. Кривые второго порядка
- •Тема 3. Уравнение плоскости
- •Тема 4. Взаимное расположение прямой и плоскости
- •Тема 5. Функция. Область определения
- •Тема 6. Непрерывность функции. Предел функции
Модуль 2. Аналитическая геометрия на плоскости и пространстве. Понятие функции
Тема 1. Прямая на плоскости
1.
Даны две точки:
![]() и
и
![]() .
Составить уравнение прямой, проходящей
через точку Q
перпендикулярно
вектору
.
Составить уравнение прямой, проходящей
через точку Q
перпендикулярно
вектору
![]() .
.
2. Составить уравнение прямой, если точка служит основанием перпендикуляра, опущенного из начала координат на эту прямую.
3.
Даны вершины треугольника:
![]() ,
,
![]() ,
,
![]() .
Составить уравнения его высот.
.
Составить уравнения его высот.
4.
Даны уравнения сторон треугольника
![]() ,
,
![]() ,
,
![]() .
Определить точку пересечения его высот.
.
Определить точку пересечения его высот.
5.
Даны вершины треугольника:
![]() ,
,
![]() ,
,
![]() .
Составить уравнение перпендикуляра,
опущенного из вершины А
на медиану, проведенную из вершины В.
.
Составить уравнение перпендикуляра,
опущенного из вершины А
на медиану, проведенную из вершины В.
6. Написать уравнение прямой, проходящей через начало координат прямоугольной системы Oxy и наклоненной к оси Ox под углом:
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() ; 4)
; 4)
![]() .
.
8. Написать уравнение прямой, проходящей через начало координат:
параллельно прямой
 ;
;перпендикулярно прямой
 ;
;образующей угол
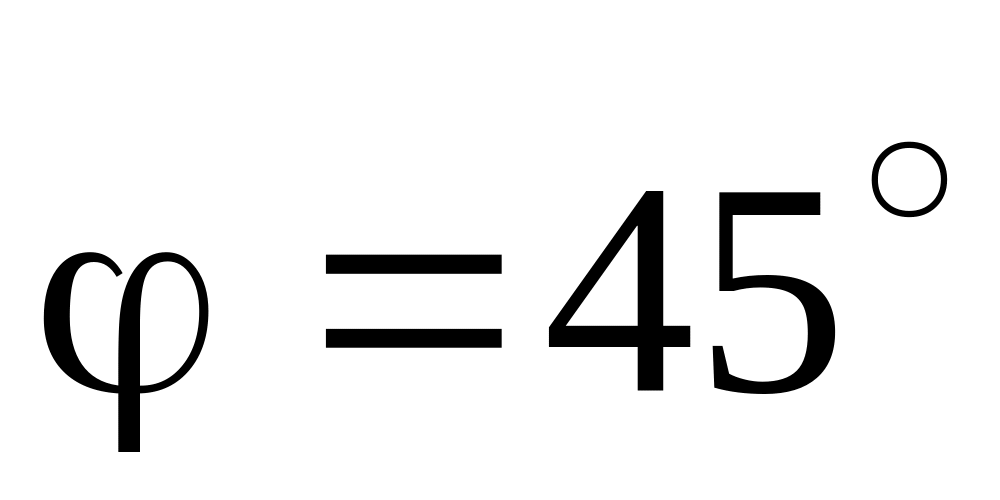 с прямой
с прямой
 ;
;наклоненной под углом в
 к прямой
к прямой
 .
.
9.
Написать уравнение прямой, проходящей
через точку
![]() параллельно:
параллельно:
1)
оси абсцисс; 2) биссектрисе координатного
угла; 3) прямой
![]() .
.
10.
Найти уравнение прямой, проходящей
через точку
![]() и составляющей с осью Ox
угол вдвое больше угла, составленного
с этой осью прямой
и составляющей с осью Ox
угол вдвое больше угла, составленного
с этой осью прямой
![]() .
.
11.
Составить уравнение прямой, проходящей
через точку
![]() параллельно прямой:
параллельно прямой:
1)
![]() ;
;
2)
![]() .
.
12.
Составить уравнение прямой, проходящей
через точку
![]() на одинаковом расстоянии от точек
на одинаковом расстоянии от точек
![]() и
и
![]() .
.
13.
Найти точку
![]() ,
симметричную точке
,
симметричную точке
![]() относительно прямой, проходящей через
точки
и
относительно прямой, проходящей через
точки
и
![]() .
.
14. Определить угол между прямыми:
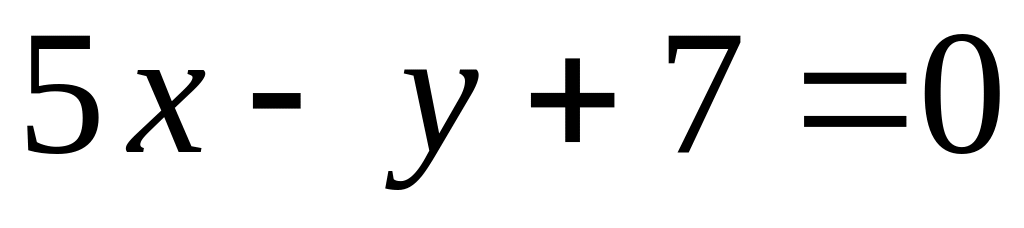 ,
,
 ;
; ,
,
 ;
; ,
,
 ;
; ,
,
 .
.
15. Установить, какие из следующих прямых перпендикулярны:
1)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ; 4)
; 4)
![]() .
.
16.
Даны две противоположные вершины
квадрата:
![]() и
и
![]() .
Составить уравнение его сторон.
.
Составить уравнение его сторон.
17.
Точка
![]() является центром квадрата, одна из
сторон которого лежит на прямой
является центром квадрата, одна из
сторон которого лежит на прямой
![]() .
Составить уравнения остальных сторон
квадрата.
.
Составить уравнения остальных сторон
квадрата.
18.
Даны уравнения сторон треугольника
![]() ,
,
![]() ,
,
![]() .
Доказать, что этот треугольник
равнобедренный.
.
Доказать, что этот треугольник
равнобедренный.
19.
Точка
![]() является вершиной квадрата, одна из
сторон которого задана уравнением
является вершиной квадрата, одна из
сторон которого задана уравнением
![]() .
Вычислить площадь этого квадрата.
.
Вычислить площадь этого квадрата.
20.
Даны уравнения двух сторон прямоугольника
![]() ,
,
![]() и одна из его вершин
и одна из его вершин
![]() .
Вычислить площадь этого квадрата.
.
Вычислить площадь этого квадрата.
21. Вычислить расстояние между параллельными прямыми:
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]()
Тема 2. Кривые второго порядка
1. Составить каноническое уравнение эллипса, зная, что:
а)
полуоси его
![]()
б)
расстояние между фокусами
![]() а большая ось
а большая ось
![]()
в)
малая полуось
![]() и расстояние между фокусами
и расстояние между фокусами
![]()
г)
большая полуось
![]() а эксцентриситет
а эксцентриситет
![]()
д)
малая полуось
![]() а эксцентриситет
а эксцентриситет
![]()
е)
сумма полуосей
![]() а расстояние между фокусами
а расстояние между фокусами
![]()
2.
Написать
каноническое уравнение эллипса, если
известно, что: а)
расстояние между фокусами равно 8, а
малая полуось b=3;
б) большая полуось a=6,
а эксцентриситет
![]() ;
в)
расстояние между фокусами равно 6, а
эксцентриситет
;
в)
расстояние между фокусами равно 6, а
эксцентриситет
![]() ;
г) расстояние между фокусами равно 6, а
;
г) расстояние между фокусами равно 6, а
![]() ;
д)
расстояние между фокусами равно
;
д)
расстояние между фокусами равно
![]() ,
а
,
а
![]() .
.
3.
Найти
длины осей, координаты фокусов и
эксцентриситет эллипса
![]()
4.
Написать
каноническое уравнение гиперболы, если
известно, что: а)
расстояние между фокусами 2c=10,
а между вершинами 2а=8;
б)
действительная полуось
![]() ,
а эксцентриситет
,
а эксцентриситет
![]() ;
в)
расстояние между фокусами 2с=6,
а эксцентриситет
;
в)
расстояние между фокусами 2с=6,
а эксцентриситет
![]() ;
г)
расстояние между фокусами 2с=20,
а уравнение асимптот
;
г)
расстояние между фокусами 2с=20,
а уравнение асимптот
![]() ;
д)
мнимая полуось b=4,
а расстояние между фокусами 2с=10.
;
д)
мнимая полуось b=4,
а расстояние между фокусами 2с=10.
5.
Построить
гиперболу
![]() Найти:
а)
действительную и мнимую полуоси; б)
координаты фокусов; в)
эксцентриситет; г)
уравнения асимптот.
Найти:
а)
действительную и мнимую полуоси; б)
координаты фокусов; в)
эксцентриситет; г)
уравнения асимптот.
6. Составить каноническое уравнение гиперболы, если расстояние между вершинами ее равно 20, а расстояние между фокусами 30.
7.
Действительная
полуось гиперболы равна 5, эксцентриситет
![]() Найти уравнение гиперболы.
Найти уравнение гиперболы.
8.
Построить
гиперболу
![]() Найти:
а)
действительную и мнимую полуоси; б)
координаты фокусов; в)
эксцентриситет; г)
уравнения асимптот.
Найти:
а)
действительную и мнимую полуоси; б)
координаты фокусов; в)
эксцентриситет; г)
уравнения асимптот.
9.
Найти
уравнения асимптот гиперболы
![]()
10.
Построить
эллипс
![]() Найти: а)
полуоси; б)
координаты фокусов; в)
эксцентриситет.
Найти: а)
полуоси; б)
координаты фокусов; в)
эксцентриситет.
11.
Уравнения
асимптот гиперболы
![]() и
и
![]() ,
а расстояние между фокусами
,
а расстояние между фокусами
![]() Найти уравнение гиперболы.
Найти уравнение гиперболы.
12.
Парабола
![]() проходит через точку А(2,4).
Определить ее параметр p.
проходит через точку А(2,4).
Определить ее параметр p.
13. Составить уравнение параболы, зная, что вершина ее находится в начале координат и расстояние от фокуса до вершины равно 4 единицам длины, а осью симметрии служит ось Оx.
14.
Найти
полуоси, координаты фокусов, эксцентриситет
эллипса, если известно, что эллипс
проходит через точки
![]() и
и
![]()
15.
Эллипс
проходит через точки
![]() и
и
![]() .
Написать его уравнение и найти расстояния
точки М
от фокусов.
.
Написать его уравнение и найти расстояния
точки М
от фокусов.
16.
Гипербола
проходит через точку
![]() и
имеет мнимую полуось b=2.
Написать ее уравнение и найти расстояния
точки М
от фокусов.
и
имеет мнимую полуось b=2.
Написать ее уравнение и найти расстояния
точки М
от фокусов.
17.
Построить
параболу
![]() .
Найти а)
координаты фокуса; б)
уравнение директрисы.
.
Найти а)
координаты фокуса; б)
уравнение директрисы.
18. Написать уравнение параболы: а) проходящей через точки (0;0) и (1;-3) и симметричной относительно оси Оx; б) проходящей через точки (0;0) и (2;-4) и симметричной относительно оси Оy.
19.
Написать
уравнение параболы и уравнение директрисы,
если известно, что парабола симметрична
относительно оси Оx
и что точка пересечения прямых
![]() и
и
![]() лежит на параболе.
лежит на параболе.
20.
Найти фокальные радиусы
![]() и
и
![]() для эллипса
для эллипса
![]() ,
если точка М(-4,2,4)
принадлежит эллипсу.
,
если точка М(-4,2,4)
принадлежит эллипсу.
21.
Фокусы эллипса расположены на оси
абсцисс, симметрично относительно
начала координат. Точка
![]() принадлежит эллипсу, а его малая полуось
принадлежит эллипсу, а его малая полуось
![]() Найти большая полуось
Найти большая полуось
![]() .
.
