Вопрос 1.

Физи́ческая величина́ — физическое свойство материального объекта, физического явления, процесса, которое может быть охарактеризовано количественно.

Значение физической величины — число, вектор, или в самом общем случае тензор, характеризующие эту физическую величину, с указанием единицы измерения, на основе которой эти числа, вектор или тензор были определены.

Размер физической величины — число (числа), фигурирующие в значении физической величины.

Размерность физической величины — единица измерения физической величины. Как правило, у физической величины много различных размерностей: например, у длины - нанометр, миллиметр, сантиметр, метр, километр, миля, дюйм, парсек, световой год и т.д. Часть таких единиц измерения (без учёта своих десятичных множителей) могут входить в различные системы физических единиц - СИ, СГС и др.

Часто физическая величина может быть выражена через другие, более основополагающие физические величины. (Например, сила может быть выражена через массу тела и его ускорение)

Размерная физическая величина — физическая величина, для определения значения которой нужно применить какую-то единицу измерения этой физической величины. Подавляющее большинство физических величин являются размерными.

Безразмерная физическая величина — физическая величина, для определения значения которой достаточно только указания её размера. Например, спин электрона в атоме - это безразмерная физическая величина.

Скалярная физическая величина — физическая величина, валентность (ранг) тензора которой равна нулю. Это означает, что данная физическая величина может быть охарактеризована одним числом. Примеры скалярных физических величин:

Работа силы; Масса; Энергия;

Векторная физическая величина — физическая величина, валентность (ранг) тензора которой равна 1. С точки зрения обыденных представлений, как правило, это означает то, что она характеризуется некоторым направлением в пространстве.[Такие величины удобно описывать при помощи векторов. С точки зрения линейной алгебры любой вектор — это упорядоченный набор чисел (координат). К векторным физическим величинам относятся как величины, описываемые истинными векторами, так и псевдовекторами  — величинами, изменяющими знак при замене ориентации системы координат на противоположную:

примеры векторных физических величин: сила; скорость; импульс;

примеры псевдовекторных физических величин:

угловая скорость; момент импульса;

Аналоговая физическая величина – физическая величина, которая может принимать бесконечное количество размеров в заданном диапазоне ее измерения. Результат аналогового измерения всегда содержит ошибку.

Дискретная физическая величина – физическая величина, которая может принимать только конечное число размеров в заданном диапазоне ее измерения. Ее можно измерить абсолютно точно.

Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.

Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.

Сложение векторов

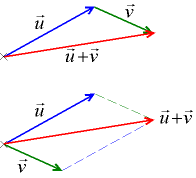
А модуль (длину) вектора суммы определяют по теореме косинусов где  — угол между векторами, когда начало одного совпадает с концом другого. Так же используется формула теперь  — угол между векторами выходящими из одной точки.

Произведение вектора на число

Произведением вектора и числа λ называется вектор, обозначаемый (или ), модуль которого равен , а направление совпадает с направлением вектора , если , и противоположно ему, если . Если же , или вектор нулевой, тогда и только тогда произведение  — нулевой вектор.

Скалярное произведение

Скалярным произведением векторов и называют число, равное , где  — угол между векторами и . Обозначения: или .

Если один из векторов является нулевым, то несмотря на то, что угол не определён, произведение равно нулю.

Свойства скалярного произведения векторов:

 — коммутативность.

 — дистрибутивность.

 — линейность по отношению к умножению на число.

Векторное произведение

Векторным произведением вектора a на вектор b называется вектор c, удовлетворяющий следующим требованиям:

длина вектора c равна произведению длин векторов a и b на синус угла φ между ними

вектор c направлен так, что тройка векторов abc является правой.

Обозначение:

Геометрически векторное произведение есть ориентированная площадь параллелограмма, построенного на векторах , представленная псевдовектором, ортогональным этому параллелограмму.

Свойства векторного произведения:

При перестановке сомножителей векторное произведение меняет знак (антикоммутативность), т.е

Векторное произведение обладает сочетательным свойством относительно скалярного множителя, то есть

Векторное произведение обладает распределительным свойством: