
- •Міністерство освіти та науки України одеський національний університет ім.І.І.Мечнікова
- •Методичні вказівки з курсу “Вища математика. Ч.I: Лінійна алгебра і аналітична геометрія” для студентів 1-го курсу епф
- •Одеса 2006
- •Лінійна алгебра
- •Лінійна алгебра
- •1.Метод Гаусса розв’язування систем лінійних алгебраїчних рівнянь
- •2. Матриці і дії над ними.
- •3. Визначники та їх основні властивості.
- •Правило Крамера для розв`язування систем лінійних рівнянь.
- •Обернена матриця. Матричний спосіб розв`язання систем лінійних алгебраїчних рівнянь.
- •Ранг матриці. Теорема Кронекера-Капеллі.
- •7. Лінійні векторні простори.
- •8.Лінійна залежність векторів.
- •Скалярний добуток двох векторів.
- •Векторний добуток двох векторів в .
- •Змішаний добуток трьох векторів в
- •Аналітична геометрія
- •12. Рівняння прямої на площині.
- •13. Кут між двома прямими на площині. Умови паралельності і перпендикулярності двох прямих.
- •Площина в просторі .
- •15. Кут між двома площинами. Умови паралельності і перпендикулярності площин в
- •16. Пряма лінія у тривимірному просторі.
- •17. Кут між двома прямими, а також прямою і площиною в . Паралельність і перпендикулярність прямих і площин.
- •Криві другого порядку.
- •19. Гіпербола
- •20. Парабола
- •Література
Скалярний добуток двох векторів.
Для наочних просторів скалярним добутком двох векторів і називається число, що дорівнює добутку їхніх довжин на косинус кута між ними:
![]() .
.
У вимірному просторі скалярний добуток двох векторів і визначається такою рівністю:
![]() . (9.1)
. (9.1)
Властивості скалярного добутку:
1.
![]()
2.
![]()
3.
![]() ;
;
4. Якщо
![]() то
то
![]()
![]()
За допомогою скалярного добутку довжину вектора можна визначити як
![]()
Вектор, що має одиничну довжину, називається ортом. Для кожного ненульового вектора існує вектор такого ж напрямку, довжина якого дорівнює одиниці:
![]() .
.
Два вектори називаються ортогональними, якщо їх скалярний добуток дорівнює нулю. На площині і у 3-вимірному просторі
![]() ,
,
тому для ортогональних векторів косинус кута між ними дорівнює нулю і поняття ортогональності і перпендикулярності збігаються.
Якщо в лінійному просторі визначено скалярний добуток двох векторів за правилом (9.1) із властивостями 1-4, то лінійний простір називається евклідовим.
В евклідовому просторі виконується так звана нерівність Буняковського-Коші-Шварца:
![]() .
.
Векторний добуток двох векторів в .
Векторним
добутком двох векторів
![]() називається вектор
називається вектор
![]() такий, що
такий, що
а)
![]()
в)
![]() площа паралелограма, побудованого на
векторах
площа паралелограма, побудованого на
векторах
![]() ;
;
с) якщо
![]() то вектори
утворюють праву трійку.
то вектори
утворюють праву трійку.
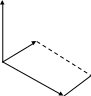
Рис.2
Упорядкована трійка некомпланарних векторів називається правою, якщо з кінця третього вектора найкоротший поворот від першого вектора до другого здійснюється проти обертання годинникової стрілки.
Згідно
з умовою в), вектор
![]() тоді і тільки тоді, коли вектори
колінеарні.
тоді і тільки тоді, коли вектори
колінеарні.
Властивості векторного добутку:
1.
![]()
2.
![]() ;
;
3.![]() ;
;
В координатній формі векторний добуток обчислюється за формулою:
![]() ,
де
,
де
![]()
Приклад
1. Обчислити площу
трикутника
![]() якщо
якщо
![]()
Розв`язання.

Рис.3
За означенням векторного добутку двох векторів площа паралелограма, побудованого на двох неколінеарних векторах, дорівнює модулю векторного добутку цих векторів. Тому площу трикутника АВС можна обчислити за формулою:
![]() .
.
Залишилося знайти координати векторів:
![]() .
.
Отже маємо:
![]() ;
;
![]() ;
;
![]()
Змішаний добуток трьох векторів в
Змішаним
добутком векторів
![]() називається число
називається число
![]() .
.
Властивості змішаного добутку:
1.
![]() ;2.
;2.
2.
![]() ;
;
3.
![]() ;
;
4.
геометрично
![]() ,
де
,
де
![]() об`єм паралелепіпеда,
побудованого на векторах
;
знак “+” відповідає
правій трійці векторів, а “-“ – лівій.
об`єм паралелепіпеда,
побудованого на векторах
;
знак “+” відповідає
правій трійці векторів, а “-“ – лівій.
В координатній формі змішаний добуток обчислюється за формулою:
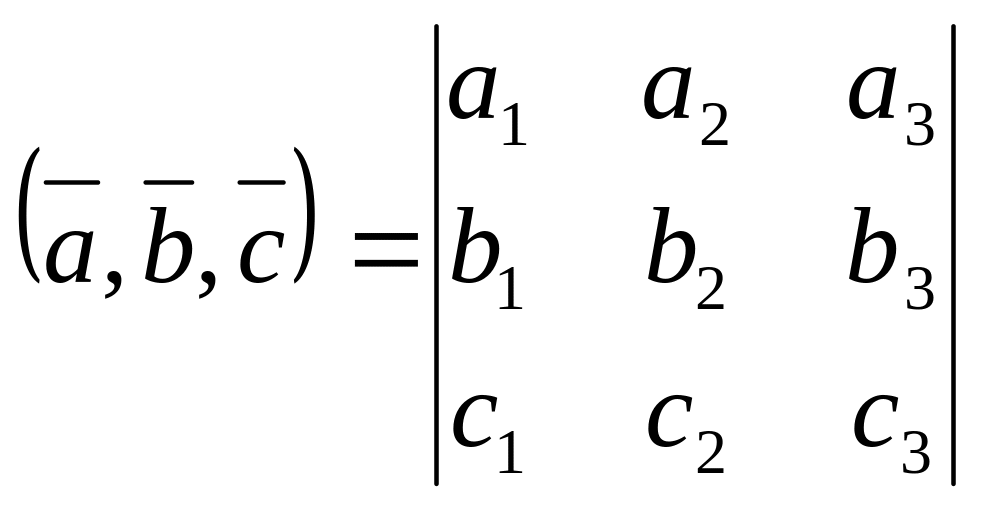 ,
де
,
де
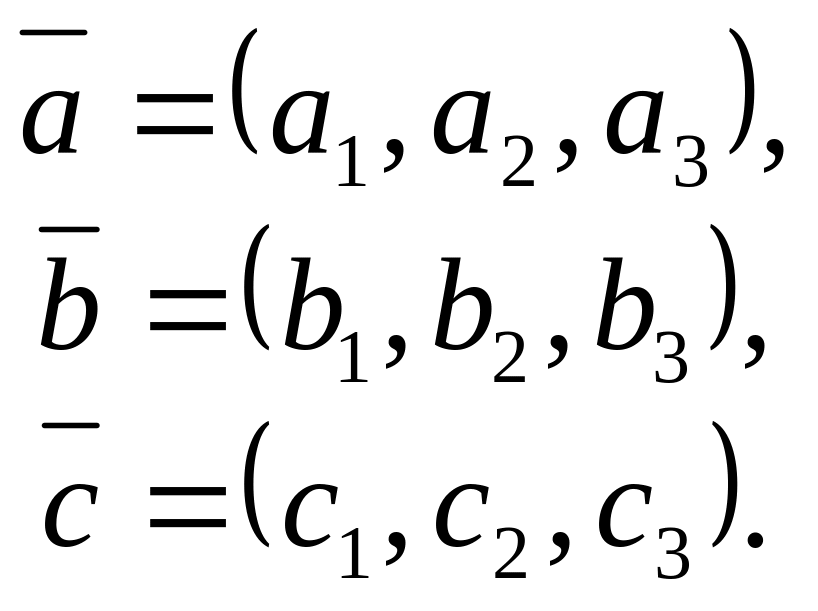
Згідно з умовою 4, змішаний добуток векторів дорівнює нулю тоді і тільки тоді, коли вектори компланарні.
Зауваження. Операції векторного та змішаного добутку визначені тільки в 3-вимірному просторі .
Приклад 1. Визначити, чи будуть лінійно залежними вектори
![]() .
.
Розв`язання.
Обчислимо змішаний добуток векторів
![]()

тобто дані вектори лінійно залежні.
