Лабораторная работа №4 Определение отношения теплоемкостей по скорости звука в газе.

Студент должен знать: уравнение Клапейрона-Менделеева, первое начало термодинамики, выражение для внутренней энергии идеального газа через число степеней свободы, виды теплоемкостей, значения молярных теплоемкостей при изопроцессах (V=const, p=const, T=const) и при адиабатическом процессе, уравнение Пуассона для адиабатического процесса, природу звука в газе, расчетную формулу для нахождения  по скорости звука в газе, способы измерения скорости звука по резонансу в воздушном столбе.

Студент должен уметь: работать с электроприборами, измерять скорость звука по резонансу в воздушном столбе.

Краткая теория Теплоемкость газов.

При термодинамическом равновесии состояние газа в целом может характеризоваться тремя параметрами: давлением P, объемом V и температурой Т.

Соотношение, связывающее между собой эти величины, называется уравнением состояния газа. Для идеального газа таковым является уравнение Клапейрона - Менделеева, которое для данной массы газа m имеет вид:

,

где  - молярная масса газа,

R- универсальная газовая постоянная.

При равновесном переходе газа из одного состояния в другое, т.е. при термодинамическом процессе, должно выполниться первое начало термодинамики, которое можно сформулировать следующим образом:

количество теплоты dQ, переданное газу, идет на изменение его внутренней энергии dU и на работу dA, совершаемую газом против внешних сил: dQ = dU + dA

Элементарная работа dA=pdV, а внутренняя энергия одного киломоля идеального газа определяется по формуле

, (1)

где i - число степеней свободы молекулы газа,

Для одноатомных молекул i=3 (только 3 поступательных степени свободы); для двухатомных i=5 (3 поступательных и 2 вращательных); для трех и более атомных i=6 (3 поступательных и 3 вращательных).

Теплоёмкостью С называется величина, равная отношению сообщенного телу при нагревании количества теплоты dQ к вызванному этим процессом изменению температуры dT:

Различают удельную теплоемкость C_уд – теплоёмкость одного килограмма газа в молярную С_ - теплоёмкость одного киломоля газа. Эти теплоёмкости связаны между собой равенством:

Теплоемкости для одного и того же газа не являются постоянными величинами, а зависят от характера процесса, при котором происходит нагревание газа, т.к. одному и тому же изменению температуры dT могут соответствовать различные значения работы dA.

Рассмотрим основные изопроцессы, протекающие в одном киломоле идеального газа и найдем соответствующие им теплоёмкости.

а) Изохорический процесс (V= const)

В этом случае dV=0, следовательно dA=0, и всё подводимое к газу количество теплоты идет на увеличение его внутренней энергии dU:

dQ = dU.

Тогда молярная теплоемкость при постоянном объёме, учитывая (I), равна:

. (2)

б) Изобарический процесс (p = const)

В этом случае молярная теплоемкость

. (3)

Из уравнения состояния газа для одного киломоля имеем:

. (4)

Т.к, p = const,то dp =0 и pdV=RdT. (4а)

Подставляя (4а) в (3) и заменяя dU согласно (2) на , получим окончательно:

. (5)

в) Изотермический процесс (T = const)

В этом случае dT =0 и dQ = dA,т.е. все подводимое количество теплоты вдет на совершение газом работы, а его внутренняя энергия остается постоянной. Т.к. температура при этом не изменяется, то молярная теплоёмкость равна .

3. Адиабатический процесс (dQ =0, dU + dA =0) – процесс, происходящий при отсутствии теплообмена между газом и окружающей средой. Т.к. при этом dQ =0,то молярная теплоёмкость равна нулю.

Выведем уравнение адиабатического процесса (уравнение Пуассона).

dA = -dU или pdV = -C_vdT. (6)

Разделив равенство (4) на (6), учитывая (5),получим:

или , (7)

где - отношение теплоемкостей, называемое показателем адиабаты.

Если вместо С_р и С_v подставить в выражение для  их значения через число степеней свободы идеального газа i, то получим:

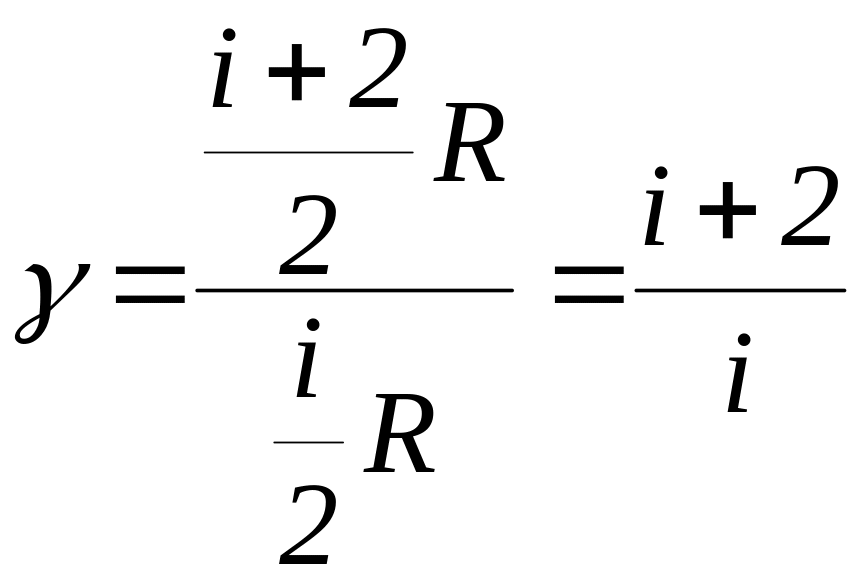. (8)

Интегрируя и потенцируя уравнение (7), получим уравнение Пуассона:

. (9)

В данной работе определяется отношение  для воздуха по скорости звука в нем.