
- •Предназначено для студентов, обучающихся по специальностям: 220201 – Управление и информатика в технических системах;
- •230105 – Программное обеспечение вычислительной техники и автоматизированных систем.
- •Содержание
- •Основные теоремы интегрального исчисления
- •Переменного и его свойства
- •§ 2. Теорема Коши
- •§ 3. Неопределенный интеграл
- •§ 4. Интегральная формула Коши и ее приложения.
- •§5 Некоторые теоремы аналитических функций
- •Глава 2 функциональные ряды в комплексной области
- •§1. Числовые ряды
- •§2. Функциональные ряды.
- •§3. Степенные ряды.
- •§4. Ряды Тейлора.
- •§5.Ряды по целым отрицательным степеням
- •§6 Ряды Лорана
- •§7 Ряд Лорана в окрестности особой точки.
- •§8 Нули аналитических функций
- •Алгоритм нахождения нулей аналитических функций и определения их порядков.
- •Глава 3 особые точки функций косплексного переменного.
- •§1 Изолированные особые точки функций
- •§2 Определение типа особых точек для суммы, разности, произведения и частного функций
- •Глава 4 вычеты и их применение
- •§ 1. Определение вычета
- •§ 2. Вычисление вычетов в полюсе и устранимой особой точке
- •§3 Вычисление контурных интегралов с помощью вычетов
- •Учебное издание Адамушко Надежда Николаевна Теория функций комплексного переменного
- •140402, Г. Коломна мо, ул. Октябрьской революции, д. 408
§ 4. Интегральная формула Коши и ее приложения.
Пусть
Г
кусочно-гладкая граница односвязной
области D
и f(z)
– функция, аналитическая в области D
и непрерывная
в замкнутой области
![]() Рассмотрим произвольную точку
Рассмотрим произвольную точку
![]() .
За исключением точки
.
За исключением точки
![]() функция переменной
функция переменной
![]() аналитична всюду в области D.
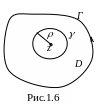
Опишем окружность
аналитична всюду в области D.
Опишем окружность
![]() радиуса ρ с центром в z,
принадлежащую области D
(рис. 1.6).
радиуса ρ с центром в z,
принадлежащую области D
(рис. 1.6).
Так
как функция f(z)
аналитична в двухсвязной области,
ограниченной кривыми Г
и
![]() ,
и непрерывна на ее границе
,
и непрерывна на ее границе
![]() ,
то по теореме Коши
,
то по теореме Коши
![]() ,
т.е. интеграл
,
т.е. интеграл
![]() не зависит от радиуса р
окружности. Так как существует
не зависит от радиуса р
окружности. Так как существует
![]() ,
то доопределив функцию
,
то доопределив функцию
![]() в точке
в точке
![]() ,
положив
,
положив
![]() ,
имеем функцию
,
непрерывную в области D,
а значит и ограниченную в ней:
,
имеем функцию
,
непрерывную в области D,
а значит и ограниченную в ней:
![]() .
Учитывая это, получим:
.
Учитывая это, получим:
![]() В силу произвольности р
и постоянства M,
имеем:
В силу произвольности р
и постоянства M,
имеем:
![]() следовательно
следовательно
![]() или
или
![]() отсюда
получаем интегральную формулу Коши:
отсюда
получаем интегральную формулу Коши:
![]() .Она
выражает значение функции f(z),
аналитической в области D
и непрерывной в
.Она
выражает значение функции f(z),
аналитической в области D
и непрерывной в
![]() ,
через ее значения на границе области
Г.
Интеграл
,
через ее значения на границе области
Г.
Интеграл
![]() называют интегралом Коши.
называют интегралом Коши.
Пример 1.
Вычислить
интеграл
![]()
Поскольку
функция
![]() аналитична в замкнутой области,
ограниченной окружностью
аналитична в замкнутой области,
ограниченной окружностью![]() ,
то по интегральной формуле Коши имеем:
,
то по интегральной формуле Коши имеем:
![]()
Если
рассмотреть этот же интеграл, но в
качестве контура взять окружность
![]() то
то
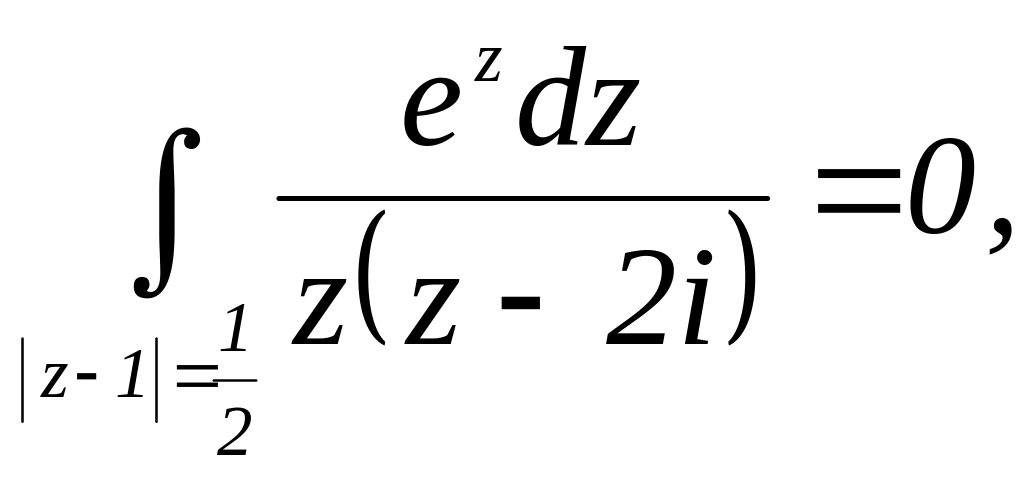 следовательно, подынтегральная функция
аналитична всюду в замкнутой области,
ограниченной окружностью
следовательно, подынтегральная функция
аналитична всюду в замкнутой области,
ограниченной окружностью
Следствие 1.
В
частном случае, если кривая
![]() является окружностью с центром в точке
z
радиуса R,
тогда
является окружностью с центром в точке
z
радиуса R,
тогда
![]() ,
следовательно,
,
следовательно,
![]()
таким
образом, функция f
(z)
равна среднему арифметическому значению
f
(![]() )
на окружности с центром z.
)
на окружности с центром z.
Интегральная
формула Коши справедлива и для многосвязной
области. Действительно, пусть D
многосвязная область, ограниченная
контуром
![]() и функция f
(z)
аналитична в D
и непрерывна
.
Рассмотрим произвольную точку
и функция f
(z)
аналитична в D
и непрерывна
.
Рассмотрим произвольную точку
![]() и такую окружность CR,
с центром в точке
и такую окружность CR,
с центром в точке
![]() ,
чтобы область, ограниченная окружностью
CR
, вместе с самой окружностью полностью
принадлежала D
(рис.1.7).
,
чтобы область, ограниченная окружностью
CR
, вместе с самой окружностью полностью
принадлежала D
(рис.1.7).
Т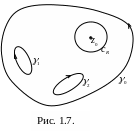 огда
функция
огда
функция
![]() удовлетворяет условиям теоремы Коши в
(n
+ 2)-связной
области, ограниченной контуром
удовлетворяет условиям теоремы Коши в
(n
+ 2)-связной
области, ограниченной контуром
![]() тогда, по доказанной выше теореме
тогда, по доказанной выше теореме
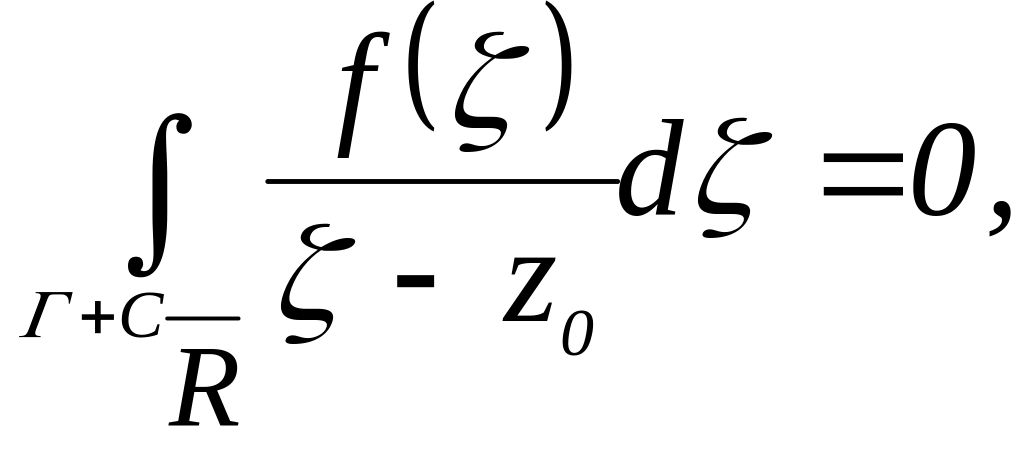
 ,
,
![]()
Используя представление функции интегралом Коши (1.11), покажем, что аналитическая в области функция дифференцируема в точках области D сколько угодно раз.
Теорема.
Если функция f (z) аналитична в области D с границей Г и непрерывна в области , то она обладает в области D производными всех порядков, причем производная порядка n представляется формулой
![]() .
(1.12)
.
(1.12)
 Доказательство.
Доказательство.
Пусть z – произвольная точка области D (рис.1.8).
На
основании интегральной формулы Коши
имеем
![]()

![]() Оценим разность
Оценим разность
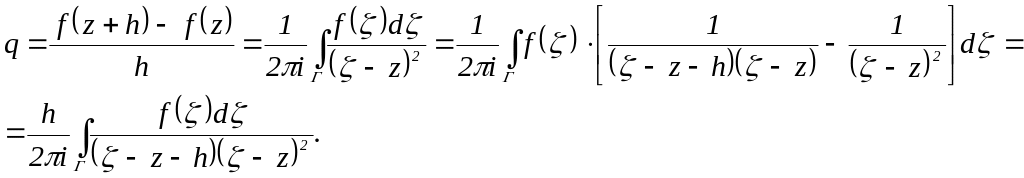
Из
непрерывности
f
(z)
на замкнутом множестве Г
следует ограниченность f
(z),
следовательно, существует М>0
такое, что
![]() < М
для
< М
для
![]() С другой стороны
С другой стороны
![]() поэтому существует
поэтому существует
![]() такое, что
такое, что
![]() .
Откуда для
.
Откуда для
![]() справедливо
справедливо
![]() ,
поэтому
,
поэтому
![]() где
l
− длина кривой Г.
Поскольку M,
l,
d
не зависят от
R,
то при
где
l
− длина кривой Г.
Поскольку M,
l,
d
не зависят от
R,
то при
![]()
![]() ,
,![]() Мы доказали формулу (1.12) для n
= 1.Для любого n
> 1 формула доказывается индукцией по
n.
Мы доказали формулу (1.12) для n
= 1.Для любого n
> 1 формула доказывается индукцией по
n.
Пример 2.
Вычислить![]()
К этому интегралу можно применить формулу (1.12), тогда
![]()
Замечание:
Рассмотрим неравенства Коши.
Обозначим
через М
максимум
![]() в
области D,
через R
расстояние от точки z
до границы и через l
длину границы Г,
тогда из интегральной формулы для n-ой
производной имеем
в
области D,
через R
расстояние от точки z
до границы и через l
длину границы Г,
тогда из интегральной формулы для n-ой
производной имеем
![]() (1.13)
(1.13)
В
частности, если
![]() аналитична
в круге
аналитична
в круге
![]() ,
то принимая в качестве D
этот круг, будем иметь:
,
то принимая в качестве D
этот круг, будем иметь:
![]() (n
= 0, 1, 2…). (1.14)
(n
= 0, 1, 2…). (1.14)
Неравенства (1.13) и (1.14) называются неравенствами Коши.
