§ 2. Вычисление вычетов в полюсе и устранимой особой точке
В рассмотренных выше примерах при нахождении вычетов функции раскладывались в ряды Лорана. При этом знание типа особой точки, в которой вычисляется вычет функции, не является обязательным. Таким методом всегда определяется вычет в тех случаях, когда заранее предполагается, что особая точка — существенно особая точка для функции. В случае устранимой особой точки и полюсов задачу вычисления можно заменить некоторыми практически более удобными формулами и правилами. Вывод этих формул и правил в общем виде связан с исследованием разложения функции в ряд в окрестности особой точки, а тип особой точки определяется по поведению функции, т.е. вычислением предела.
Если
и
─
конечная особая точка, то в разложении
функции в ряд Лорана в окрестности
,
отсутствует главная часть, следовательно,
и
Если
т.е.
−полюс
функции
то
можно определить порядок полюса, не
прибегая к разложению функции в ряд и
используя утверждение 4.3. Пусть точка
─
полюс порядка n
функции, тогда разложение функции в
ряд в окрестности точки имеет вид
,
.
Умножив обе части этих равенств на
и продифференцировав результат (n-1)
раз, получим выражение
,из
которого определяем
при
n =1
.
Последнее равенство принимает наиболее
удобную форму для функции вида
,
где
аналитические функции в точке z0
и
,а именно:
.
Результат приведенных рассуждений запишем в виде утверждения.
Утверждение
1. Если конечная особая точка z0
является устранимой особой точкой
функции , то 
устранимая
особая точка. (4.5)
2.Если
─полюс
порядка n
функции ,
то
─полюс
порядка n
(4.6)
─
простой полюс.
(4.7)
3. Если
─простой
полюс. функции
где
аналитические
функции в точке z0
и
то
(4.8)
Замечание
Формула (4.7) дает следующий алгоритм вычисления вычета функции в полюсе порядка n .
1.Умножить на
,
где n
порядок полюса z0,
и получить функцию
2. Найти производную функции порядка
:
3. В соответствии с (4.7) найти
Пример 1. Найти вычеты в конечных особых точках функций:
а)
б)
в)
а) Конечныe особые точки z1=-1 и z2 =3 ─ простые полюсы, поэтому используя
формулу (4.8),можно найти вычеты функции в указанных точках в виде
б) для функции
особые точки
и
.
1) Точка ─простой полюс и выполняются
условия применимости формулы (4.8) . При
этом функцию удобно представить в виде
.
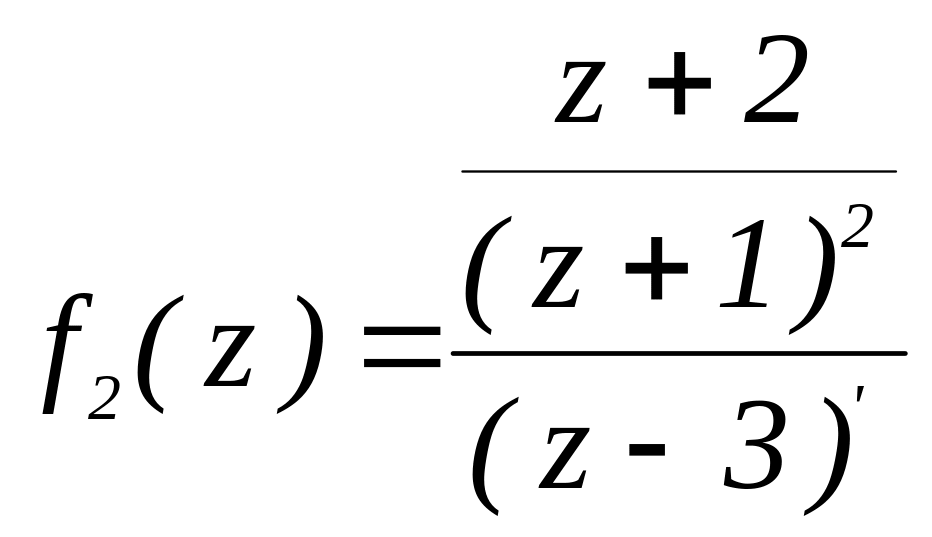Применяя формулу (4.8), находим
2) Точка z2 =-1 для полюс второго порядка. Применяя формулу (4.6) при n= 2,
запишем решение согласно алгоритму
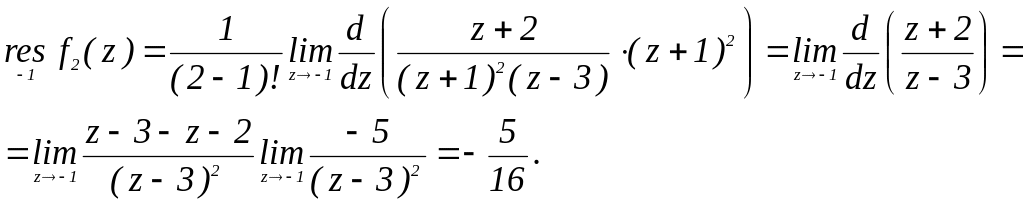
в) Для функции
единственная конечная особая точка─
устранимая особая точка
,
поэтому согласно формуле (4.5)
Все полученные результаты соответствуют результатам примеров 1 и 2 §1.
Пример 2. Найти вычеты следующих функций в особых точках:
а)
б)
Особыми точками функций являются нули
знаменателя ─корни уравнения
или
, находим
и два других корня квадратного уравнения
,т.е.
,
.
а)Для
все три особые точки ─простые
полюсы.
Находим вычеты в них по формуле (4.8):
что можно проверить, разложив
в
ряд в окрестности z=∞
т.е. в области
.
б) Для
точка
─устранимая
особая точка, так как
,
поэтому
.
2)Точки и ─простые полюсы, поэтому вычеты находим, как и в предыдущем случае или по формуле (4.7):
Вычет функции в z=∞ можно получить по формуле (4.4):
В заключение рассмотрим вычет в бесконечно удаленной точке в случае, когда она является устранимой особой точкой для . Разложение функции в ряд Лорана имеет вид
Коэффициент 
можно
определить из этого равенства следующим
образом:
Так как
,
то доопределим функцию, положив
Получаем формулу для вычисления вычета
в точке
─
устранимой особой точке функции
(4.9)
В частности, если
является нулем функции
,т.е.
,
то формула принимает вид
.
(4.10)
Пример 3. Найти вычеты в функций:
a)
б)
а) Точка
─устранимая
особая точка этих функций и
.
Поэтому
вычеты этих функций находим по формуле
(4.26):
Результат совпадает с полученным в примере 1(а) §2.
б) Точка
─устранимая
особая точка для
,
так как
.
Вычет находим по формуле (4.9):
