
- •Гл. 1. Матрицы и системы линейных алгебраических уравнений. § 1. Матрицы.
- •§ 2.Сложение матриц и произведение матрицы на число.
- •Свойства линейных операций.
- •§ 3.Умножение матриц.
- •Свойства произведения матриц.
- •§4. Транспонирование матрицы.
- •Свойства операции транспонирования.
- •§5. Обратная матрица
- •Алгоритм построения обратной матрицы.
- •§ 6. Ранг матрицы
- •Свойства ранга матрицы
- •§ 7. Элементарные преобразования матрицы.
- •§8. Матричная запись системы линейных алгебраических уравнений.
- •§ 9. Метод Гаусса.
- •§ 10. Разрешимость слау. Теорема Кронекера-Капелли.
- •§ 11. Исследование однородных слау.
- •§ 12.Понятие линейной зависимости и линейной независимости .
- •Список использованной литературы.
Гл. 1. Матрицы и системы линейных алгебраических уравнений. § 1. Матрицы.
Определение 1.
Таблица, содержащая m-строк
и n –столбцов называется
матрицей А и обозначается![]()
А=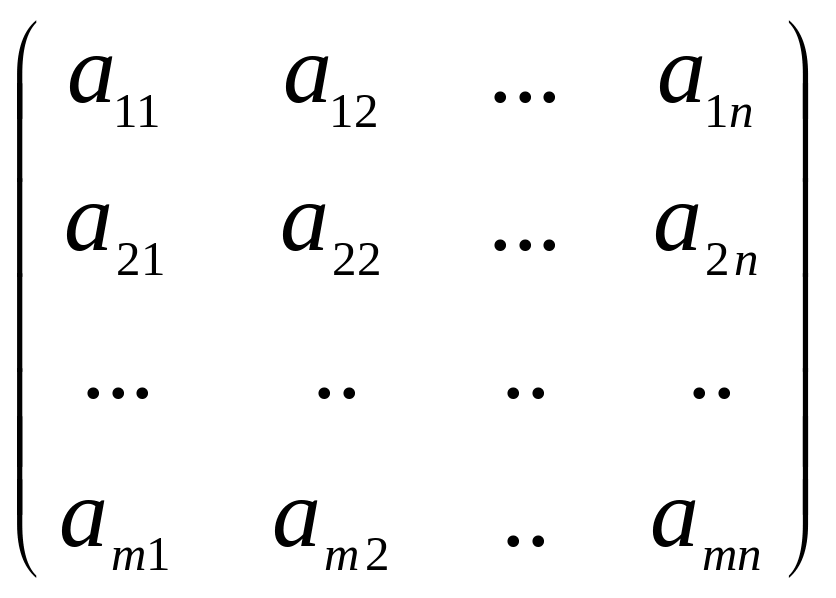 либо А =
либо А =
![]() ,
,
![]()
Числа m и n называются размерами матрицы.
Определение 2.
Если m
![]() n
, то матрица называется прямоугольной.
Если m =n, то
матрица называется квадратной. Если m
= 1, получается матрица – строка, если
n = 1, матрица – столбец.
n
, то матрица называется прямоугольной.
Если m =n, то
матрица называется квадратной. Если m
= 1, получается матрица – строка, если
n = 1, матрица – столбец.
Например, А= матрица размерами 3
матрица размерами 3![]() 2,
В=
2,
В=![]() матрица
размерами 2
3.А,
В – прямоугольные матрицы, Е=
матрица
размерами 2
3.А,
В – прямоугольные матрицы, Е= - квадратная матрица 3 порядка,
- квадратная матрица 3 порядка,
С=(1 2 3) матрица-строка,
D=![]() матрица-столбец.
матрица-столбец.
Определение 3. Матрица, все элементы которой равны нулю, называют нулевой.
Определение 4. Квадратная матрица называется невырожденной, если ее определитель отличен от нуля. В противном случае матрица вырождена.
А=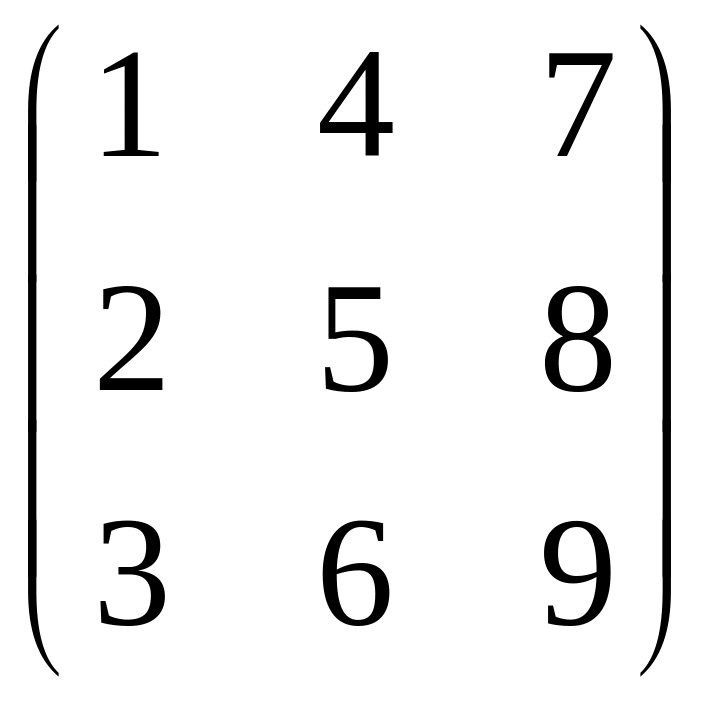 вырожденная квадратная матрица,
С=
вырожденная квадратная матрица,
С=
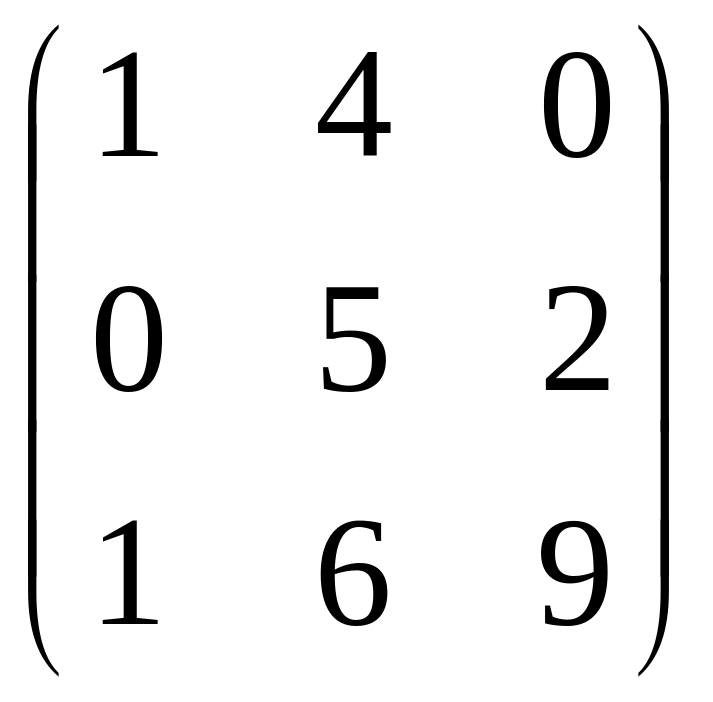 - невырожденная.
- невырожденная.
Определение
5. Место
расположение элементов с одинаковыми
номерами называют главной диагональю.
Элементы
![]() стоят на главной диагонали.
стоят на главной диагонали.
Определение 6 . Диагональной называется квадратная матрица, у которой все элементы вне главной диагонали равны нулю.
Например, А=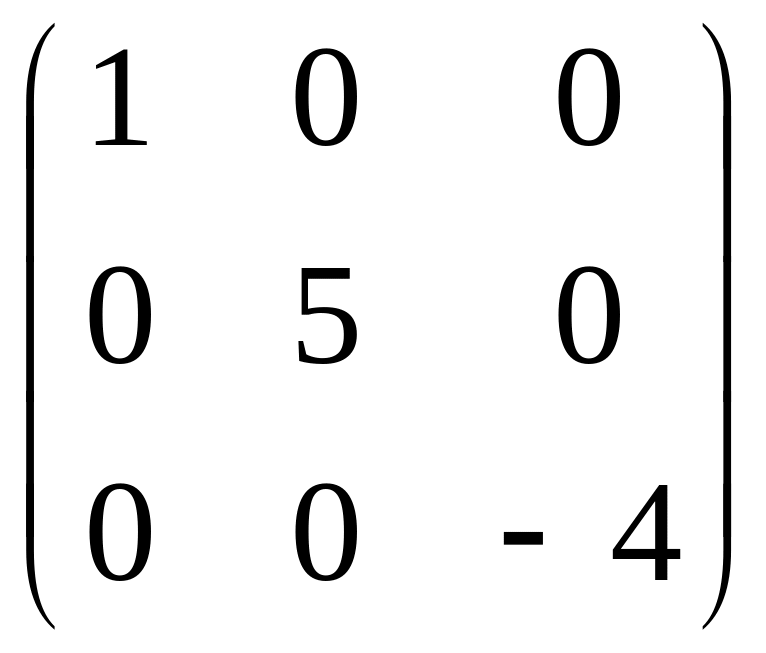 ,
В=
,
В=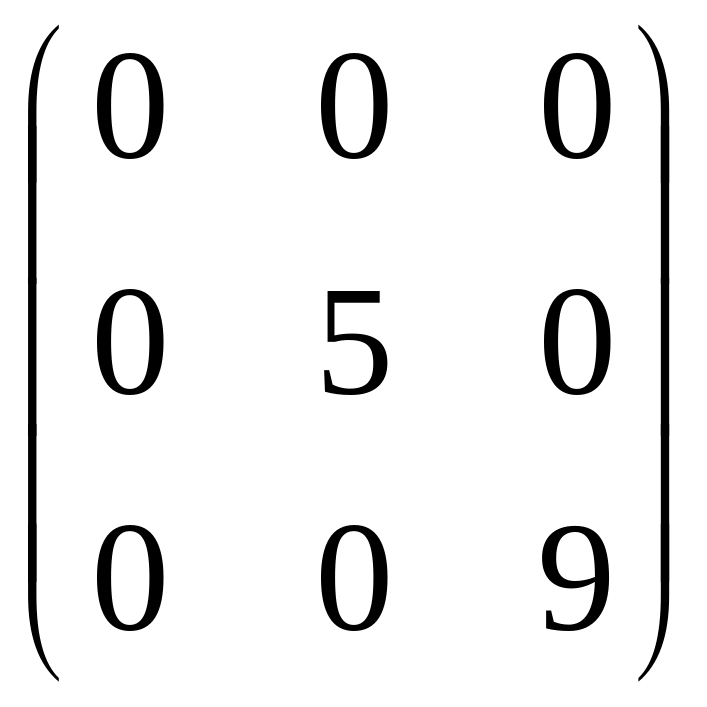 диагональные.
диагональные.
Определение 7. Единичной матрицей называется диагональная матрица, у которой на главной диагонали стоят единицы.
Е= единичная матрица третьего порядка. Единичная матрица 2-го порядка:
Е=
![]() .
.
Определение
8. Квадратная
матрица А называется симметричной,
если величины элементов симметричных
относительно главной диагонали равны,
т. е.
![]()
А=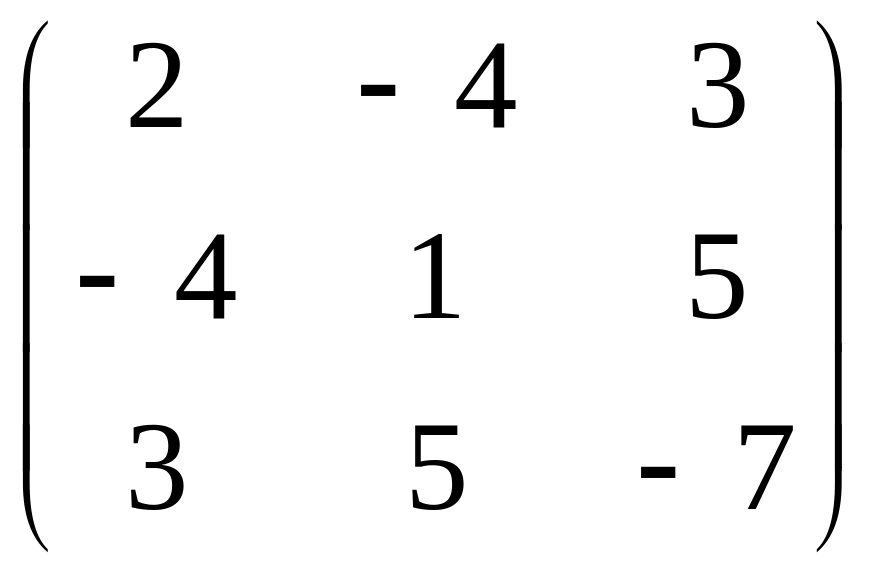 симметричная матрица, В=
,
С=
несимметричные матрицы.
симметричная матрица, В=
,
С=
несимметричные матрицы.
Определение
9. Квадратная
матрица называется нижней (верхней)
треугольной, если все ее элементы
![]() <
<![]() (
(
![]() >
).
>
).
A=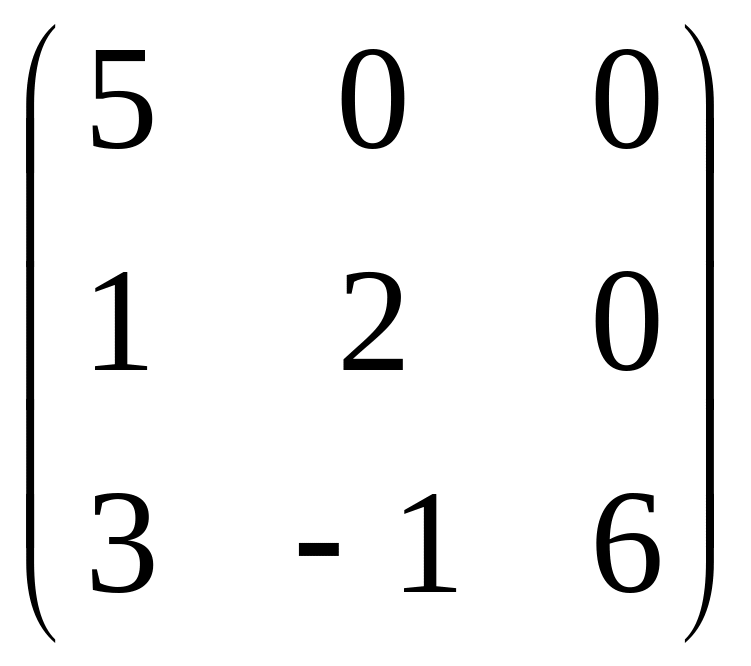 - нижняя треугольная, В=
- нижняя треугольная, В= - верхняя треугольная матрицы.
- верхняя треугольная матрицы.
§ 2.Сложение матриц и произведение матрицы на число.
Определение 1.
Пусть даны две матрицы А=
и В=
![]() размерами m
n.
Говорят, что матрицы равны А = В,
если,
размерами m
n.
Говорят, что матрицы равны А = В,
если,
![]()
Пусть даны две матрицы А= и В= размерами m n.
Матрица С размерами m n называется суммой матриц А и В, если ее элементы равны сумме соответствующих элементов матриц А и В
С=А+В
![]()
![]()
Например А=
,
В=![]() ,
тогда С=
,
тогда С=![]() .
.
Определение 2.
Пусть дана матрица В =
размерами m
n
и число
![]() .
.
Произведением числа
![]() на матрицу В называется матрица С
размерами m
n,
каждый элемент которой равен произведению
соответствующего элемента матрицы В
на число
.
на матрицу В называется матрица С
размерами m
n,
каждый элемент которой равен произведению
соответствующего элемента матрицы В
на число
.
С =
В
![]()
Напрмер, если С=
, то 3С=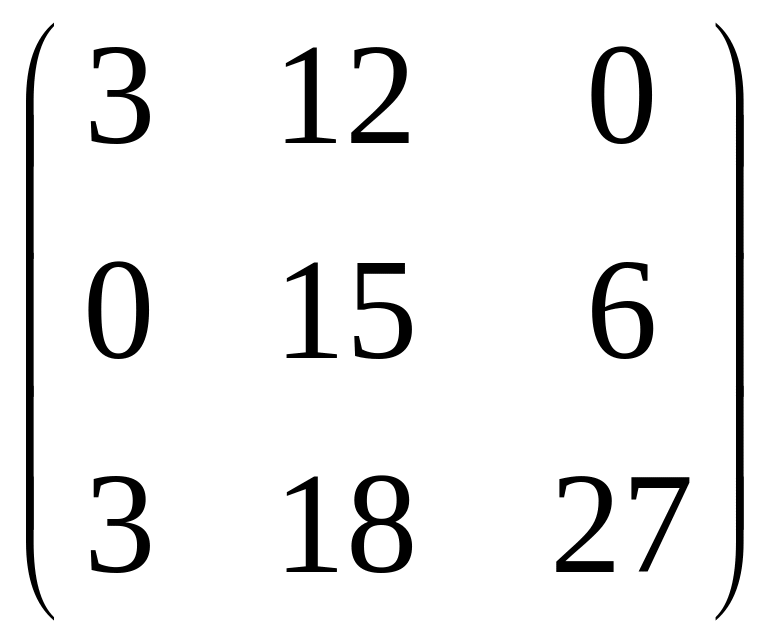 ,
-2С=
,
-2С=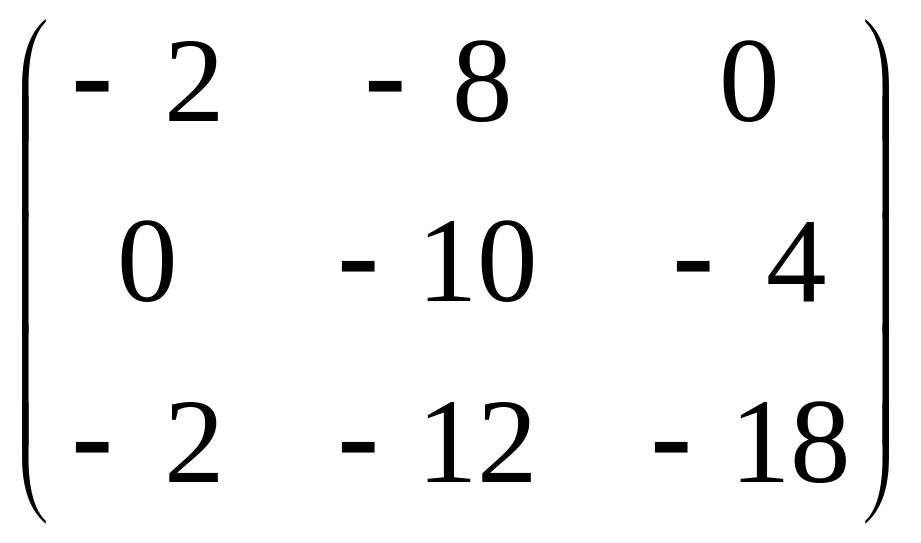
Заметим, что 2А=А+А, а разность матриц А – В = А + ( -1 )В.
Сложение матриц и умножение матрицы на число называют линейными операциями над матрицами .
Свойства линейных операций.
1. А+В = В+А
2. (А+В)+С = А+(В+С)
3.
![]()
4.
![]()
5.
![]()
6.
![]()
§ 3.Умножение матриц.
Определение 1.Пусть
даны матрицы A = (![]() размерами m
p,
и В=
размерами m
p,
и В=![]() ,
,![]() размерами p
n.
размерами p
n.
Произведением матриц называется матрица
C размерами m
n
C = AB =
![]() ,
,
![]() каждый элемент которой
каждый элемент которой
![]() =
=
![]() .
.
Пример 1. Пусть А=
![]() ,
В=
,
В=
![]() , тогда существуют оба произведения АВ
и ВА, причём АВ=
, тогда существуют оба произведения АВ
и ВА, причём АВ=![]() , а ВА=
, а ВА=![]() .
.
Пример 2. Если А=![]() , В=
, В=![]() ,
то существует только произведение АВ
и оно равно
,
то существует только произведение АВ
и оно равно
АВ =
=![]() .
.
