Контрольные вопросы

1. Сформулировать определение графа.

2. Перечислить виды графов.

3. Перечислить способы задания неорграфа.

4. Пояснить понятия: инцидентность и смежность.

5. Что называется компонентой связности неорграфа?

6. Что такое степень вершины? Сформулировать теорему о сумме степеней вершин.

7. Сформулировать определение маршрута в графе.

8. Какой маршрут в неорграфе называется минимальным?

9. Перечислить виды маршрутов.

Лекция 18

ТЕМА: ЗАДАЧИ НА НЕОРИЕНТИРОВАННЫЕ ГРАФЫ

ПЛАН:

1. Поиск маршрута с минимальным числом ребер

2. Метрические характеристики неориентированного графа

3. Минимальные маршруты в нагруженных графах

4. Задачи на деревьях

5. Цикловой ранг графа. Цикломатическое число

Главная

1. Поиск маршрута с минимальным числом ребер

При решении некоторых прикладных задач нередко возникает необходимость найти маршрут, соединяющий заданные вершины в графе G(V,X). Причем маршрут должен быть кратчайшим.

Маршрут в графе G(V,X) из вершины v в вершину w, где v  w, называется минимальным, если он имеет минимальную длину среди всех маршрутов из v в w.

Напомним, что длина маршрута – это число ребер в нем.

Свойство минимального маршрута: Любой минимальный маршрут является простой цепью.

Рассмотрим задачу поиска минимального маршрута. Введем некоторые обозначения: пусть G(V,X) – граф, v  V, V₁  V; обозначим G(v) = {wV|{v, w} X} – образ вершины v; G(V₁) = - образ множества вершин V₁ ; G^-1(v) = { wV|{w, v} X} – прообраз вершины v; G^-1(V₁) = - прообраз множества вершин V₁ .

Пусть G(V,X) – граф с n  2 вершинами и v и w – заданные вершины из данного графа. Причем v  w. Опишем алгоритм поиска минимального маршрута в графе G (алгоритм фронта волны).

Шаг1. Помечаем вершину v индексом 0. затем помечаем вершины, принадлежащие образу вершины v , индексом 1. множество вершин с индексом 1 обозначим FW₁(v). Полагаем к =1.

Шаг 2. Если FWk(v) =  или выполняется к = n –1, w FWk(v), то вершина w не достижима из v, и работа алгоритма на этом заканчивается. В противном случае переходим к шагу 3.

Шаг 3. Если w FWk(v), то переходим к шагу 4. в пртивном случае существует маршрут из v в w длины к, и этот путь является минимальным. Последовательность вершин vw₁w₂…w_{k -1} w , где

w_k-1  FW_k-1G^-1(w);

w_k-2  FW_k-2G^-1(w_k-1);

……………………….

w₁  FW₁G^-1(w₂);

и есть искомый минимальный путь из v в w.

Шаг 4. Помечаем индексом к+1 все непомеченные вершины, которые принадлежат образу множества вершин с индексом к. множество вершин с индексом к+1 обозначим FW_k+1(v). Присваиваем к: = к+1 и переходим к шагу 2.

Множество FW_k(v) называют фронтом волны к- го уровня.

Замечание: Вершины w₁, w₂,…w _k-1 могут быть выделены неоднозначно, в случае, если существует несколько минимальных маршрутов из v в w.

Примеры.

1. Используя описанный алгоритм найти минимальный маршрут из v_{1 в} v₁₀ в графе, заданном диаграммой:

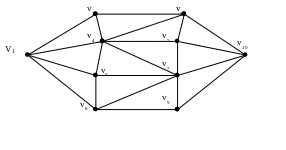
Вершине v₁ присваиваем индекс 0 и последовательно определяем

FW₁(v₁) = {v₂, v₄, v₆, v₈};

FW₂(v₁) = {v₃, v₅, v₇, v₉};

FW₃(v₁) = {v₁₀}.

Значит, существует маршрут из v₁ в v₁₀ длиной l =3 , и он является минимальным.

Найдем последовательность вершин в этом маршруте:

FW₂(v₁)G^-1(v₁₀)= {v₃, v₅, v₇, v₉} {v₃, v₅, v₇, v₉}= {v₃, v₅, v₇, v₉}, выберем любую из вершин полученного множества, например, v₇;

FW₁(v₁)G^-1(v₇) = {v₂, v₄, v₆, v₈} {v₄, v₈, v₆}= {v₄, v₈, v₆}, выберем любую вершину из этого множества – v₆ .

Получили минимальный маршрут: v₁ v₆ v₇ v₁₀. Данная задача имеет несколько решений.

2. Построить минимальный маршрут из v₁ в v₆ в графе, заданном матрицей смежности:

.

Вершине v₁ присваиваем индекс 0 и последовательно определяем множества, просматривая строки:

FW₁(v₁) = {v₂};

FW₂(v₁) = {v₃};

FW₃(v₁) = {v₄, v₅, v₆}.

Маршрут существует и равен l = 3. Найдем последовательность вершин в этом маршруте, просматривая столбцы:

FW₂(v₁)G^-1(v₆)= {v₃} {v₃, v₅}= {v₃}, включаем в маршрут единственно возможную вершину v₃;

FW₁(v₁)G^-1(v₃) = {v₂} {v₂, v₄, v₅, v₆}= {v₂}, включаем в маршрут единственно возможную вершину v₂;

Получили минимальный маршрут v₁ v₂ v₃ v₆. Задача имеет единственное решение.