Контрольные вопросы

1. Сформулировать определение бинарного отношения.

2. Описать операции, выполняемые с бинарными отношениями.

3. На множестве прямых на плоскости рассмотрим отношения: а) параллельность прямых,

б) перпендикулярность прямых. Определить будут ли эти отношения отношениями эквивалентности.

4. Дано множество: люди, живущие в одной стране. Задать какое либо отношение эквивалентности и разбить данное множество на классы эквивалентности.

5. К какому типу отношения порядка относятся следующие отношения: 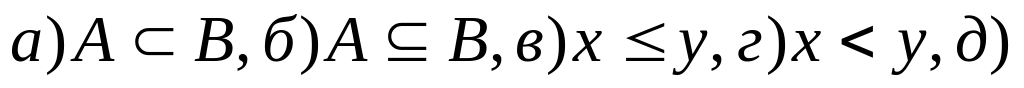схема организации подчинения в учреждениях.

Лекция 16

ТЕМА: СООТВЕТСТВИЯ И ОТОБРАЖЕНИЯ

ПЛАН:

1. Соответствие

2. Функция

3. Отображение

4. n –местная функция

5. Обратная функция

6. Свойства отображений

Главная

1. Соответствие

1.1. Основные понятия

Определение: Соответствием называется какое – либо правило, с помощью которого элементу а из множества А ставится в соответствие элемент b из множества В.

Таким образом, соответствие есть множество G пар (a; b) , где и .

Множество значений а называется областью определения, а множество значений b называется областью значений соответствия G.

Если область определения есть множество А, то соответствие называется всюду определенным.

Если область определения строгое подмножество множества А, то соответствие называется частично определенным.

Примеры:

а). Соответствие х ≤ у, где . Область определения данного соответствия , значит, соответствие всюду определенное.

б). Соответствие , где . Область определения данного соответствия х≥3, значит, соответствие частично определенное.

в). Соответствие между множеством учеников класса и действующих в школе кружков. Если каждый ученик класса посещает хотя бы один кружок, то соответствие всюду определенное, если хотя бы один ученик не посещает ни одного кружка, то соответствие – частично определенное.

Множество всех элементов называются образами а в В при данном соответствии.

Множество всех , которым соответствуют b, называются прообразами b в А при данном соответствии.

Для соответствия между множеством учеников класса и множеством кружков образами являются кружки, а прообразами – ученики.

0. Виды соответствий

Если образом элемента а из области определения является единственный элемент b из области значений, то такое соответствие называется функциональным.

Примеры:

а). , область определения – любые действительные числа, область значений – неотрицательные числа. Причем каждому х соответствует единственное у. Значит, соответствие функциональное.

б). , область определения и область значений – действительные числа, удовлетворяющие данному равенству. Но для всех х ≠ 0 из области определения соответствуют по два образа. Значит, это соответствие не является функциональным.

Всюду определенное соответствие G , область значений которого есть множество В, каждому элементу соответствует единственный образ , и каждому соответствует единственный прообраз , называется взаимнооднозначным соответствием.

Примеры:

а). у = кх + b , где область определения и область значений – действительные числа, взаимнооднозначное соответствие, т.к. каждому х соответствует единственный у и наоборот.

б). у = х² , где область определения – действительные числа, а область значений - неотрицательные числа. Не является взаимнооднозначным соответствием, т.к. любому положительному образу соответствует по два прообраза.

Заметим, что взаимнооднозначное соответствие является в свою очередь функциональным.

Рассмотрим примеры различных соответствий и определим их вид:

а). , соответствие - это все точки координатной плоскости, т.е. . Причем, для каждого прообраза х соответствует бесконечное множество образов у, и наоборот. Значит, это соответствие не является функциональным, и тем более взаимнооднозначным.

б). - круг, на границе которого отмечены точки А, В, С. Область определения – числовой отрезок [2; 4], область значений - числовой отрезок [1; 3].

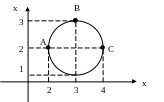
Дуга окружности АВС – является функциональным соответствием между [2; 4] и [1; 3]- каждому прообразу х соответствует единственный образ у.

Дуга окружности ВС – это взаимнооднозначное соответствие, т.к. каждому прообразу х соответствует единственный образ у и наоборот.

Круг не является функциональным соответствием, т.к. каждому прообразу х соответствует бесконечное множество образов у.

в). Позиция фигуры на шахматной доске - это взаимнооднозначное соответствие, т.к. каждому прообразу – шахматной фигуре соответствует единственная клетка – образ и наоборот.