1.2.10. Задачи оптимального управления

Постановка задачи опти­мального управления значительно сложнее, чем постановка ранее рассмотренных задач. Поэтому начнем с содержательного примера.

Рассмотрим задачу запуска ракеты в космос. Пусть плоскость орбиты фиксирована, тогда положение ракеты как материальной точки задается двумя координатами x₁, x₂, ее скорость – координа­тами x₃, x₄, масса – координатой x₅. Обозначим через u₁ величину тяги двигателя, а через u₂ – угол между направлением тяги и осью x₁. Тогда, в соответствии с законами механики, движение ра­кеты описывается следующей системой дифференциальных уравнений

, ,

(1.31)

, , ,

где p₁, p₂ – суммарные проекции внешних сил, действующих на ракету, таких как сила тяжести, сопротивление воздуха и т. д., q(u₁) – секундный расход массы, т. е. скорость расхода рабочего вещества. Ракета управляется с помощью выбора параметров управ­ления u = (u₁, u₂), которые подчинены ограничениям вида

, . (1.32)

Вектор управлений задается как функция времени u = u(t), удов­летворяющая ограничениям (1.32). Если теперь подставить и(t) в правую часть системы (1.31), то при выполнении некоторых усло­вий эта система будет иметь единственное решение х(t), определяющее состояние системы (т.е. движение ракеты) в момент t, как только заданы начальные условия х(t₀) = х⁰. Наряду с начальными могут быть заданы и конечные условия при t = Т. Например, если ракету необходимо вывести на круговую орбиту радиуса R с кру­говой скоростью V, то конечные условия примут вид:

(x₁(T))² + (x₂(T))² = R²,

x₁(T) x₃(T) + x₂(T) x₄(T) = R² , (1.33)

(x₃(T))² + (x₄(T))² = V².

Кроме того, существуют ограничения и на фазовые координаты х(t) – фазовые ограничения. Скажем, траектория ракеты не должна пересекать поверхность Земли, не должна заходить в зону радиа­ционных поясов и т. д.

Цель выбора управления u(t), удовлетворяющего условию (1.32), в задаче оптимального управления ракетой (1.31) может состоять, например, в минимизации расхода топлива

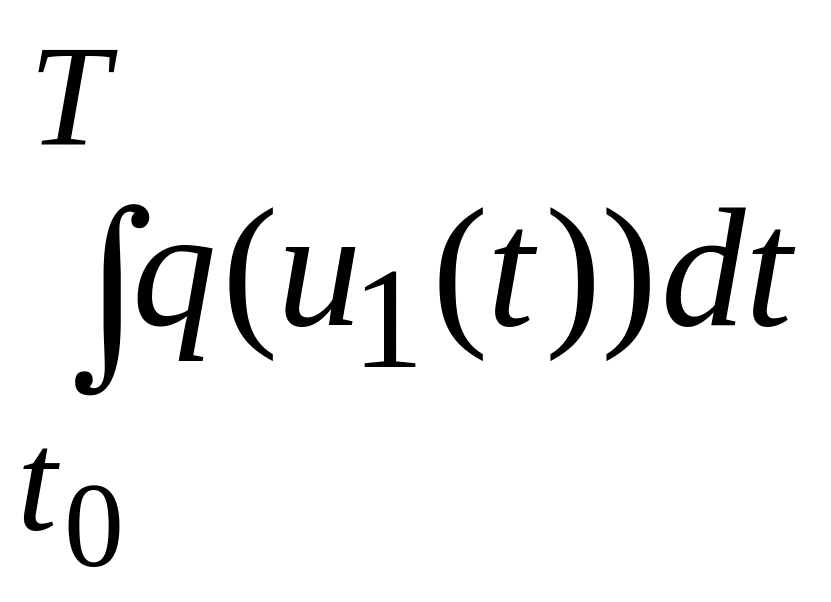. (1.34)

При этом траектория должна удовлетворять начальным и конечным условиям, а также фазовым ограничениям Можно ставить и задачу оптимального быстродействия, т. е. минимизации Т – t₀. Если же требуется вывести ракету на круговую орбиту максимального ра­диуса, то следует максимизировать функционал

(x₁(T))² + (x₂(T))² . (1.35)

Перейдем теперь к общей постановке задачи оптимального управ­ления Аналогом системы (1.31) служит здесь система дифферен­циальных уравнений

, (1.36)

описывающая движение некоторого управляемого объекта, подчинен­ное начальным условиям

x(t₀) S₀(t₀), (1.37)

конечным условиям

x(T) S(T), (1.38)

и фазовым ограничениям

x(t) X(t), t  [t₀, T]. (1.39)

Ограничения на управление можно записать в общем виде как

u(t) U(t), t  [t₀, T]. (1.40)

Здесь [t₀, T] – отрезок времени, на котором происходит управление системой (1.36), S₀(t₀), S(T), X(t), U(t), при каждом t – заданные множества из пространств соответствующих размерностей.

В качестве целевого функционала (аналога функции цели в за­даче оптимизации (1.1)) примем

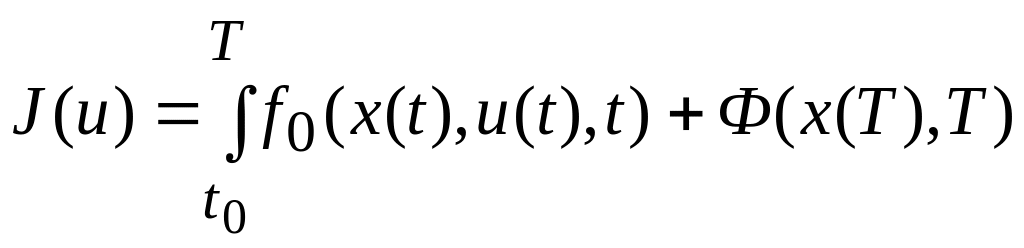. (1.41)

Очевидно, в (1.41) объединены целевые функционалы типа (1.34) и (1.35).

В соответствии с тем, что мы говорили выше, задачу оптималь­ного управления поставим как задачу минимизации функ­ционала (1.41) при ограничениях (1.36), (1.37), (1.38), (1.39), (1.40).