
- •1. Задачи оптимизации
- •1.1. Основные понятия
- •1.2. Постановка задачи оптимизации
- •1.2.1 Задача безусловной оптимизации
- •1.2.2. Задача условной оптимизации
- •1.2.3. Классическая задача на условный экстремум
- •1.2.4. Понятия выпуклого множества и выпуклой функции
- •1.2.5. Выпуклая задача оптимизации
- •1.2.6. Задача математического программирования
- •1.2.7. Задачи выпуклого программирования
- •1.2.8. Задачи линейного и квадратичного программирования
- •1.2.9. Задача дискретной оптимизации
- •1.2.10. Задачи оптимального управления
- •2.Начальные сведения о численных методах оптимизации
- •2.1. Понятие о численных методах оптимизации
- •2.2. Сходимость методов оптимизации
- •2.3. Условия остановки (критерии окончания счета)
- •2.4. Направление убывания и методы спуска
- •2.5. Выбор длины шага из условия минимизации функции вдоль заданного направления
1.2.4. Понятия выпуклого множества и выпуклой функции
Множество Х
Rn называется
выпуклым, если
![]() при всех х1, х2
X,
[0, 1]. Иными словами, множество Х выпукло,
если оно вместе с любыми своими двумя
точками х1 и х2
содержит соединяющий их отрезок,
т. е. множество вида
при всех х1, х2
X,
[0, 1]. Иными словами, множество Х выпукло,
если оно вместе с любыми своими двумя
точками х1 и х2
содержит соединяющий их отрезок,
т. е. множество вида
[x1, x2] = {x Rn | x = x2 + (x1 - x2), 0 1}
(рис. 1.4).


Рис.1.4. а) Выпуклое множество; б) невыпуклое множество
На числовой прямой R выпуклыми множествами являются всевозможные промежутки, т.е. одноточечные множества, интервалы, полуинтервалы, отрезки, полупрямые и, наконец, сама. прямая. Примерами выпуклых множеств в пространстве Rn служат само пространство, любое его линейное подпространство, одноточечное множество, шар, отрезок, а также следующие множества:
![]()
– прямая, проходящая через точку х0 в направлении вектора h;
![]()
– луч, выходящий из точки х0 в направлении h;
![]() (1.15)
(1.15)
– гиперплоскость с нормалью р;
![]() ,
,
![]() (1.16)
(1.16)
– порождаемые ею полупространства.
Все перечисленные множества, кроме шара, являются частными случаями выпуклого множества вида
X = {x Rn | Ax b} = { x Rn | ai, x bi, i = 1,…, m}, (1.17)
где A – некоторая матрица размера т п со строками a1, …, am, b = (b1, …, bm) Rm (т = 1, 2, ...). Множества вида (1.17) принято называть полиэдральными или просто полиэдрами. Таким образом, полиэдр — это множество решений некоторой системы конечного числа линейных неравенств, или, что то же самое, пересечение конечного числа полупространств.
Функция f, определенная на выпуклом
множестве
![]() ,
называется выпуклой на X, если
,
называется выпуклой на X, если
![]() (1.18)
(1.18)
при всех х1, х2 Х, [0, 1]. Если при всех х1, х2 Х, x1 x2, [0, 1] неравенство (1.18) выполняется как строгое, то f называется строго выпуклой на X. Функция f называется (строго) вогнутой, если функция – f (строго) выпукла.
Геометрически выпуклость функции f означает, что любая точка произвольной хорды графика f располагается не ниже соответствующей точки самого графика (рис.1.6, а). Для вогнутой функции взаимное расположение хорды и графика обратно (рис.1.6, б). Функции f (х) = х2, f(x) = ex выпуклы на R; f(x) = ln x вогнута на множестве положительных чисел; f(x) = sin x вогнута на [0, ] и выпукла на [, 2]. Отметим, что указанные функции, в самом деле, строго выпуклы или вогнуты. Функция f(x)= ||x|| выпукла, f(x) = ||x||2 строго выпукла на Rn. Функцию вида
f(x)= a, x + b, (1.19)
где a Rn, b R, будем называть линейной. Ясно, что для линейной функции неравенство (1.18) выполняется как равенство. Поэтому она одновременно выпукла и вогнута на Rn, но не строго.

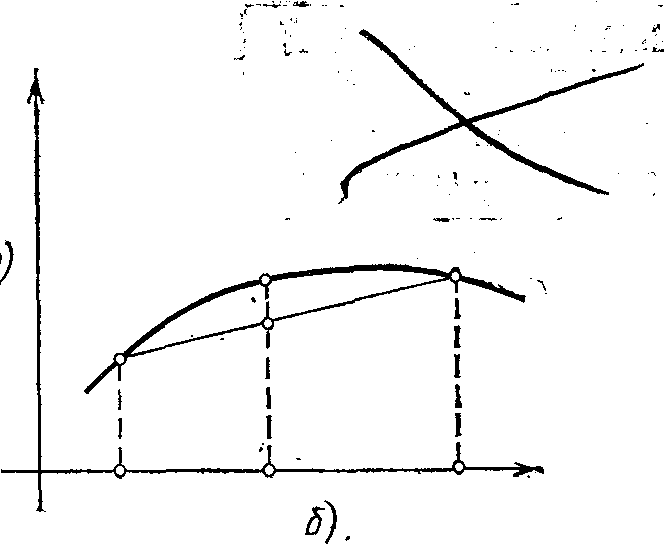
Рис. 1.6. а) Выпуклая функция; б) вогнутая функция
1.2.5. Выпуклая задача оптимизации
Задача (1.1) называется выпуклой, если X – выпуклое множество, f – выпуклая функция на X.
Теорема 1.8. Если задача (1.1) выпукла, то любое ее локальное решение является также глобальным.
Таким образом, для выпуклых задач понятия локального и глобального решений не различаются и можно говорить просто об их решении.
Второе свойство выпуклых задач можно высказать в виде следующего общего принципа: необходимые условия при соответствующих предположениях выпуклости оказываются и достаточными.
Теорема 1.9. Пусть функция f выпукла на Rn и дифференцируема в точке х* Rn. Если f'(х*) = 0, то х* – точка минимума f на X, т. е. решение задачи (1.5).
Полученные свойства выпуклых задач имеют важное значение не только в теории, но и в численных методах оптимизации. Дело в том, что большинство существующих численных методов позволяет, вообще говоря, находить лишь локальные решения, а точнее, стационарные точки задачи. Теоремы 1.8, 1.9 говорят о том, что для выпуклой задачи отыскание стационарной точки автоматически означает отыскание решения, причем глобального.
Укажем еще одно полезное свойство выпуклых задач.
Теорема 1.10. Пусть задача (1.1) выпукла
и имеет решение. Тогда множество ее
решений
![]() выпукло (рис. 1.7, а). Если при этом f
строго выпукла на X, то решение задачи
единственно, т. е. X* состоит из одной
точки (рис. 1.7, б).
выпукло (рис. 1.7, а). Если при этом f
строго выпукла на X, то решение задачи
единственно, т. е. X* состоит из одной
точки (рис. 1.7, б).

Рис.1.7. Выпуклость множества решений выпуклой задачи оптимизации
