2.4. Правило перемножування діаграм спрямованості

У відповідності з виразами (2.13) і (2.15) комплексна амплітуда результуючого вектора електричного поля всієї антени:

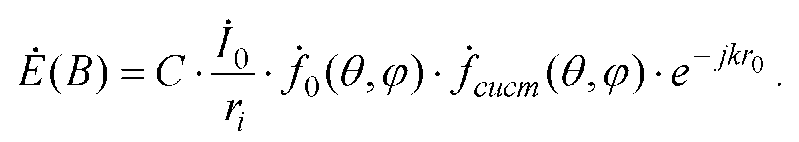(2.16)

У виразі (2.16) залежність амплітуди поля від напрямку, тобто діаграма спрямованості антени, позначувана виражається добутком двох функцій кутів спостереження - і

Отже,

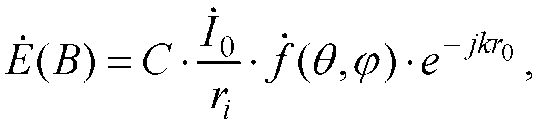
де

(2.17)

Таким чином, результуюча комплексна діаграма спрямованості системи ідентичних, однаково орієнтованих випромінювачів дорівнює добутку діаграми спрямованості одного випромінювача на множник системи.

Вираз (2.17) називається правилом перемножування діаграм спрямованості (правилом Бонч-Бруевича). Його цінність полягає в тому, що це правило застосовується до антен будь-якої конфігурації й може бути узагальнене для випадку сукупності джерел випромінювання, які не є елементарними, тобто джерел, розміри яких можуть бути порівнянні з довжиною хвилі або перевищують її.

Із цього правила наочно видний фізичний зміст множника системи. Якби елементарні випромінювачі системи не мали спрямовані властивості, тобто , то множник системи представляв би собою характеристику спрямованості системи ізотропних елементарних випромінювачів.

Таким чином, антену з гостроспрямованими властивостями можна одержати за допомогою системи слабкоспрямованих випромінювачів, якщо забезпечити необхідний множник системи. Останній можна підібрати відповідним амплітудним і фазовим розподілом живлення елементарних випромінювачів.

Розглянемо властивості множника системи випромінювачів для випадків розміщення їх на одній лінії (лінійна система) і на площині (розкрив).