- •2. Загальна теорія систем випромінювачів
- •4.1. Поняття про пряму й зворотну задачі теорії антен. Антена як система випромінювачів
- •4.2. Основні типи елементарних випромінювачів
- •4.3. Результуюче поле системи однаково орієнтованих випромінювачів у дальній зоні
- •2.4. Правило перемножування діаграм спрямованості
2. Загальна теорія систем випромінювачів
Лекція 4. Елементи теорії антен
4.1. Поняття про пряму й зворотну задачі теорії антен. Антена як система випромінювачів
У теорії антен практичне значення має рішення двох задач прямої та зворотної. Пряма задача полягає в розрахунку напруженості поля в дальній зоні по заданому розподілу амплітуд і фаз джерел поля в передавальній антені. Зворотна задача, навпаки, полягає у відшуканні струму й ЕРС на виході антени при прийманні плоскої електромагнітної хвилі, коли задані характеристики й параметри антени.
Рішення прямої задачі знаходиться досить строго, оскільки воно здійснюється на основі відпрацьованої технології застосування до практики рівнянь Максвелла. Зворотну задачу вирішити складніше, однак принцип взаємності дозволяє обмежитися рішенням прямої задачі, а отримані результати застосувати до тієї ж антени із заданими характеристиками в режимі прийому.
Таким чином, основною задачею у теорії антен є пряма, а методика її рішення зводиться до наступного.
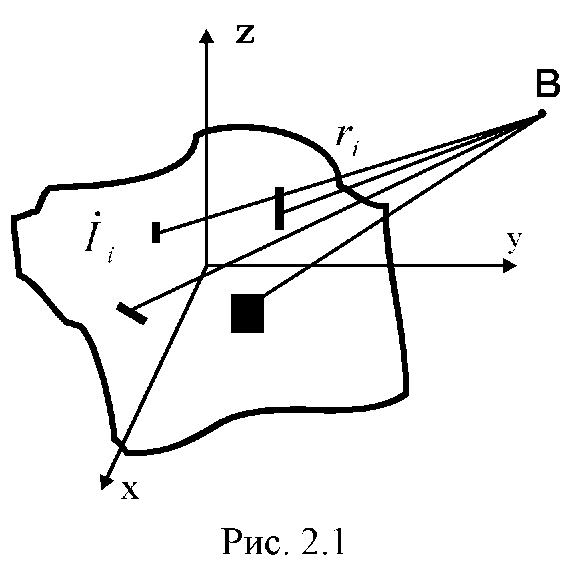
1. Вся антенна система подається у вигляді сукупності елементарних випромінювачів (рис. 2.1). Система випромінювачів може бути як дискретною, так і неперервною. Вона може бути лінійною, площинною або об'ємною. Випромінювачі в загальному випадку можуть мати різну орієнтацію й різні фізичні властивості. Для рішення задачі система випромінювачів повинна бути однозначно визначена, тобто встановлений тип кожного елементарного випромінювача, його положення в антені, орієнтація.
2. Для кожного елементарного випромінювача повинна бути задана залежно від його типу або комплексна амплітуда струму, або комплексна амплітуда напруженості поля. Розподіл цих величин по координатах антени називається амплітудно-фазовим розподілом.
3. Для
кожного елементарного випромінювача
знаходять векторну величину комплексної
амплітуди електромагнітного поля в
дальній зоні
![]()
4. Структура й величина поля, випромененого антеною, визначається як результат додавання парціальних полів, створених у довільній точці простору В всіма елементарними випромінювачами:
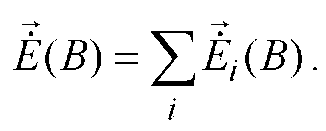 (2.1)
(2.1)
Для різнотипних випромінювачів з довільною орієнтацією в антенній системі рішення прямої задачі досить складне. Однак на практиці більша частина антен являє собою системи, що складаються з ідентичних і однаково орієнтованих випромінювачів або їх можна розглядати як такі. Для цих систем розрахунок поля істотно спрощується.
4.2. Основні типи елементарних випромінювачів
Основними типами елементарних випромінювачів, які використовуються в антенних системах, є:
елементарний електричний вібратор (диполь Герца);
випромінювач Гюйгенса;
елементарний магнітний вібратор.
Диполь
Герца
- це прямолінійний тонкий провідник,
довжина якого I
значно
менше довжини хвилі
![]() в
результаті чого високочастотний струм
у будь-якому його поперечному перерізі
в довільний момент часу має ту саму
величину й фазу. Напруженість електричного
поля в дальній зоні для елементарного
електричного вібратора визначається
виразом:
в
результаті чого високочастотний струм
у будь-якому його поперечному перерізі
в довільний момент часу має ту саму
величину й фазу. Напруженість електричного
поля в дальній зоні для елементарного
електричного вібратора визначається
виразом:
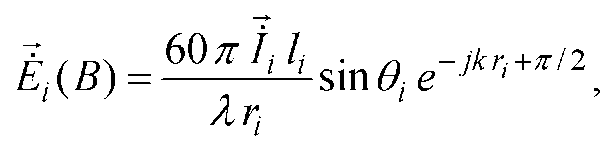 (2.2)
(2.2)
де
![]() -
вектор комплексної амплітуди струму у
вібраторі;
-
вектор комплексної амплітуди струму у
вібраторі;
![]() -
відстань від вібратора до точки далекої
зони В;
-
відстань від вібратора до точки далекої
зони В;
![]() -
довжина вібратора;
-
довжина вібратора;![]() -
кут між віссю вібратора й напрямком на
точку спостереження В;
-
кут між віссю вібратора й напрямком на
точку спостереження В;
![]() -
хвильове число.
-
хвильове число.
З
виразу (1.20)
випливає, що поляризація ЕМП, створеного
вібратором, збігається з напрямком
струму (тобто віссю вібратора), а його
діаграма спрямованості описується
функцією
![]() Оскільки
Оскільки
![]() не
залежить від кута
не
залежить від кута
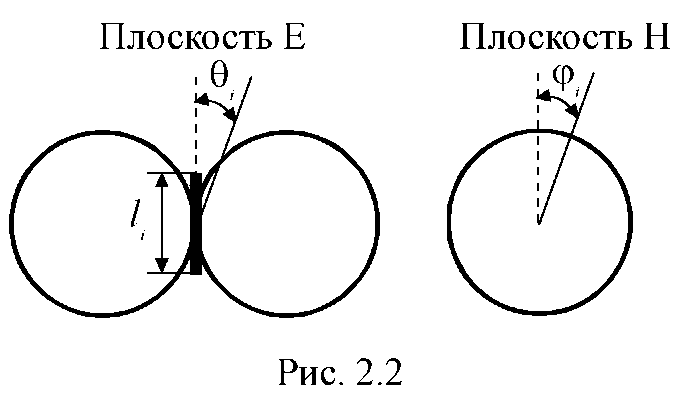
![]() тому
об'ємна ДС вібратора має форму поверхні
обертання навколо осі вібратора (форму
тора), а в
головних
перетинах - вид вісімки в площині
вібратора й окружності в перпендикулярній
йому площини (рис. 2.2).
Сукупність диполів Герца може представляти
лінійні випромінювачі різної довжини
й конфігурації.
тому
об'ємна ДС вібратора має форму поверхні
обертання навколо осі вібратора (форму
тора), а в
головних
перетинах - вид вісімки в площині
вібратора й окружності в перпендикулярній
йому площини (рис. 2.2).
Сукупність диполів Герца може представляти
лінійні випромінювачі різної довжини
й конфігурації.
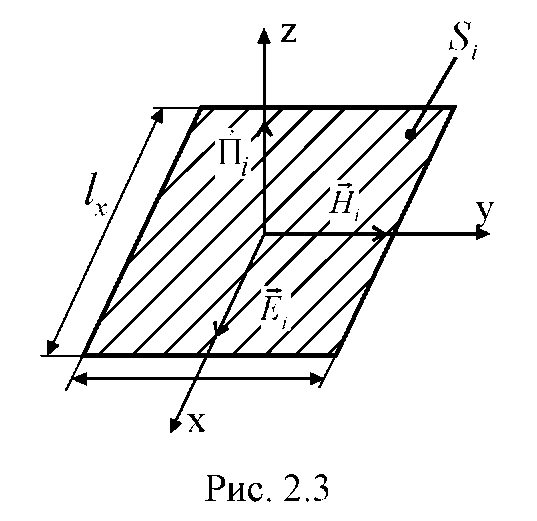
Випромінювач Гюйгенса - це гіпотетичний випромінювач, що відповідає нескінченно малій ділянці хвильового фронту плоскої ЕМХ із лінійною поляризацією (рис. 2.3).
Площа
ділянки
![]() Для
цього випадку напруженість електричного
поля в крапці В
виражається формулою:
Для
цього випадку напруженість електричного
поля в крапці В
виражається формулою:
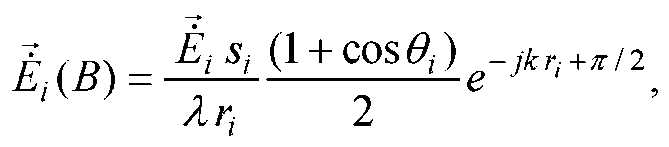 (2.3)
(2.3)
де
![]() -
вектор напруженості електричного поля
на елементі.
-
вектор напруженості електричного поля
на елементі.
Поляризація
поля збігається з напрямком
![]() Діаграма
спрямованості є тілом обертання біля
нормалі до площадки si,
описується
виразом
Діаграма
спрямованості є тілом обертання біля
нормалі до площадки si,
описується
виразом
![]() і
в головних перетинах являє собою
кардіоїду (рис. 2.4). Елементи
Гюйгенса в сукупності можуть являти
собою як поверхневі випромінювачі, так
і розкриви антен.
і
в головних перетинах являє собою
кардіоїду (рис. 2.4). Елементи
Гюйгенса в сукупності можуть являти
собою як поверхневі випромінювачі, так
і розкриви антен.
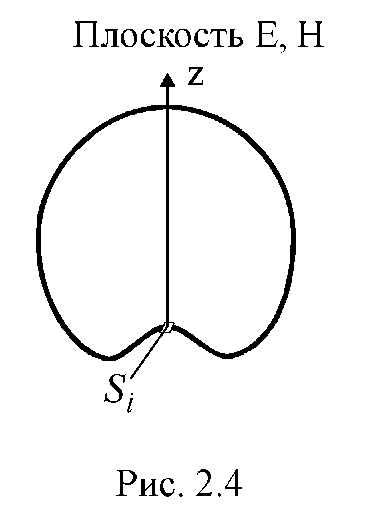
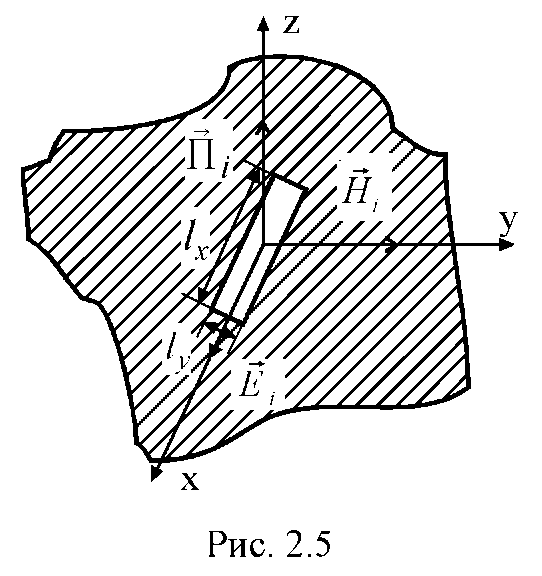
Елементарний
магнітний вібратор
(магнітний
диполь) може бути представлений у вигляді
згорнутого в кільце (або рамку)
елементарного електричного вібратора
або у вигляді щілини, прорізаної в
провідному екрані більших розмірів
паралельно вектору напруженості
магнітного поля
![]() (рис.
2.5).
(рис.
2.5).
Розміри
щілини такі, що
![]() Напруженість
електричного поля в дальній зоні
визначається залежністю:
Напруженість
електричного поля в дальній зоні
визначається залежністю:
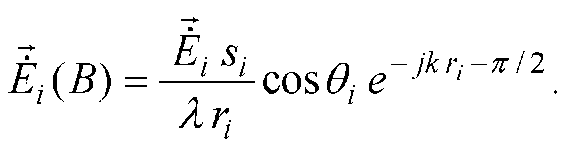 (2.4)
(2.4)
Поляризація
поля лінійна, збігається з напрямком
![]() ДС
щілинного джерела в півпросторі має
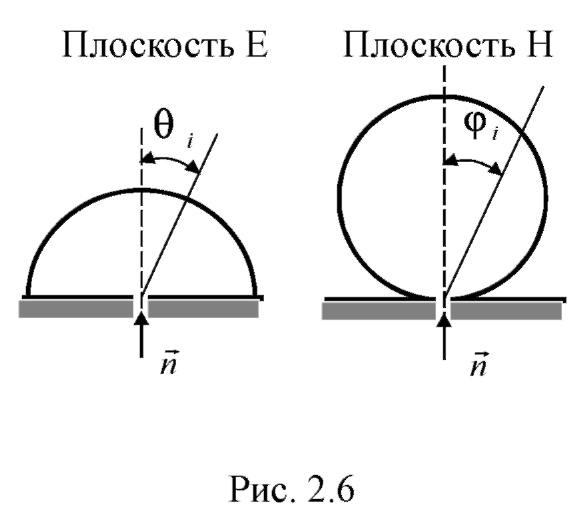
вигляд половини тора (рис. 2.6)
і виражається залежностями:
ДС
щілинного джерела в півпросторі має
вигляд половини тора (рис. 2.6)
і виражається залежностями:
![]() -
в електричній площині,
-
в електричній площині,
![]() -
у магнітній. Поле щілини максимально в
площині, перпендикулярної її осі, що
проходить через центр щілини. Уздовж
осі щілини поле дорівнює нулю.
-
у магнітній. Поле щілини максимально в
площині, перпендикулярної її осі, що
проходить через центр щілини. Уздовж
осі щілини поле дорівнює нулю.