Лабораторная работа №2. Вариант №7

Министерство образования Российской Федерации

Уфимский Государственный Авиационный Технический Университет

Кафедра ТК

Отчет по лабораторной работе №2

Исследование устойчивости и точности линейных САУ

Вариант №7

Выполнил:

Проверил:

Уфа – 2005

1. Цель работы

Изучение особенностей практического использования алгебраических и частотных критериев устойчивости для анализа динамики линейных САУ 2-го и 3-го порядков; исследование факторов, влияющих на точность линейных САУ.

2. Выполнение работы

№ варианта	7
T2, с	1,8
K4	1,3

Исследование на устойчивость линейных САУ.

1) В соответствии с вариантом задания собрать структурную схему САУ 2-го порядка (рис. 1).

g(t) ε(t) x(t)

Рис. 1

Переходная характеристика САУ h(t)

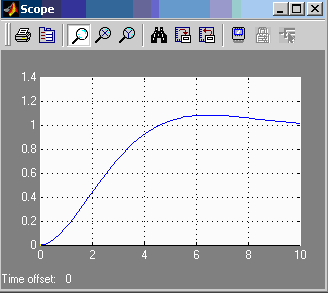
Система устойчива

h(t) устанавливается в 1.

2.2 Собрать структурную схему САУ 3-го порядка (рис. 2).

g(t) ε(t) x(t)

K₅

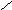
Рис. 2

Изменяя величину коэффициента K₂ и наблюдая за видом h(t), определить граничное значение , при котором САУ будет находиться на границе устойчивости (при этом K₁=K₅=1; K₃=1/K₅=1; T₃=1/K₄K₅).

К₂=1

Система устойчива

h(t) устанавливается в 1.

К₂=2.77

Изменяя величину коэффициента K₂ и наблюдая за видом h(t), определили граничное значение =2.77

К₂=4

Система неустойчива

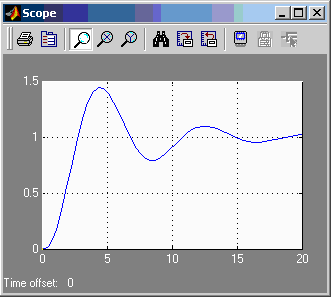
а) ЛАХ и ЛФХ разомкнутой системы для рисунка 2 К₂=К_2гр=2.77

Система на границе устойчивости

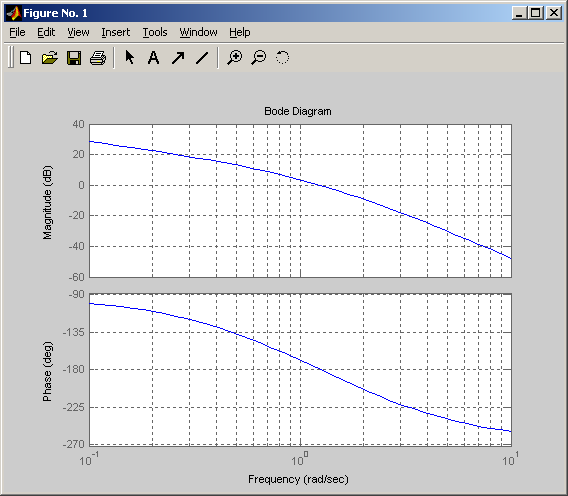
б) ЛАХ и ЛФХ разомкнутой системы К₂=К₂'=1

Запас устойчивости по модулю

Запас устойчивости по фазе

Система устойчива

в) ЛАХ и ЛФХ разомкнутой системы К₂=К₂"=4

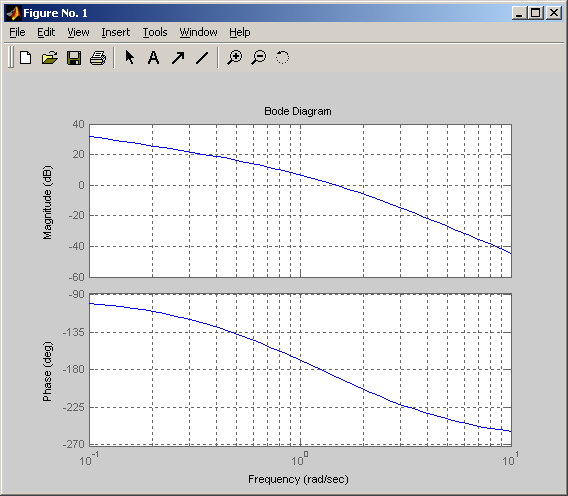
Система неустойчива

Записать передаточную функцию Ф(s) замкнутой САУ 3-го порядка (рис. 2). Используя критерий устойчивости Гурвица, исследовать систему на устойчивость при: а) б)

а)

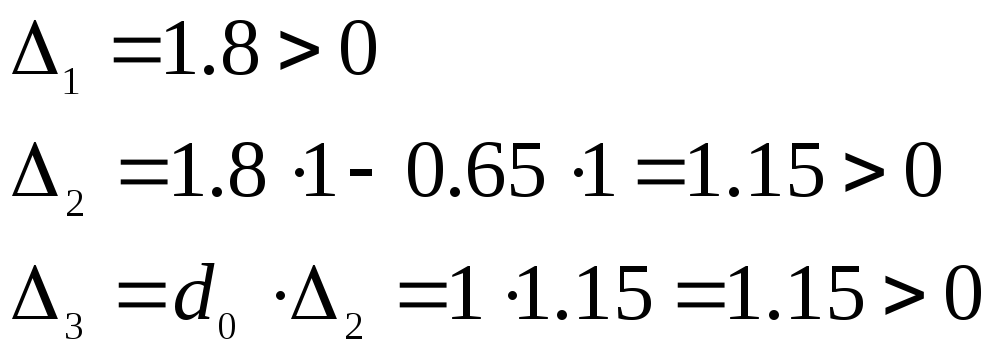
Определители матрицы коэффициентов положительны→ линейная система устойчива.

а)

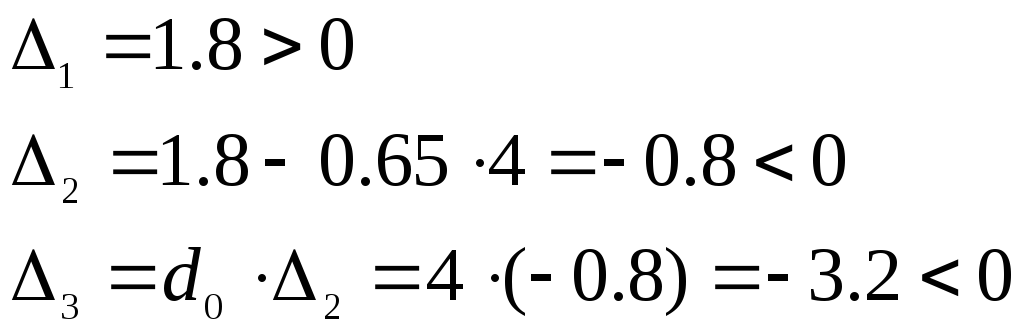
Линейная система не устойчива

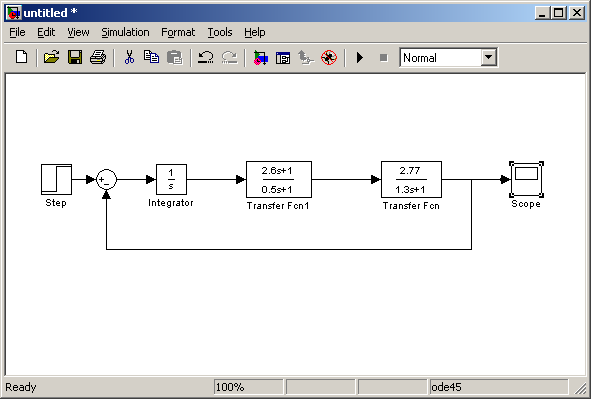
2.3 Выяснить влияние введения форсирующего звена на устойчивость САУ, для чего собрать структурную схему рис. 3 и снять график переходной функции h(t) при , T₁=2T₂.

g(t) ε(t) f(t) x(t)

Рис. 3

Переходная характеристика САУ h(t)

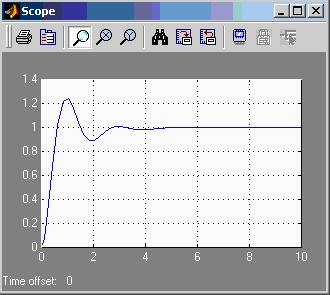
Система устойчива

Введение форсирующего звена повышает запасы устойчивости, что находит отражение на графике

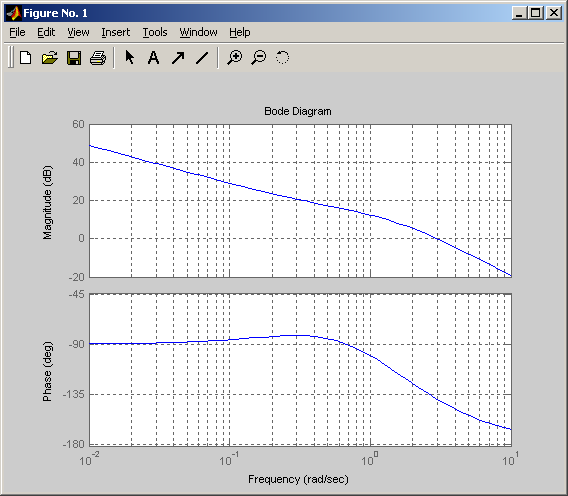
ЛАХ и ЛФХ разомкнутой системы.

ЛАХ и ЛФХ разомкнутой системы

Исследование на точность линейных САУ.

Реакция САУ на ступенчатое возмущающее воздействие g(t)=0; f(t)=1

Интегратор, не охваченный ОС

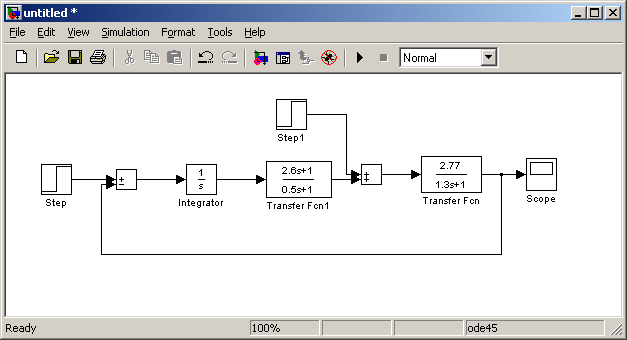
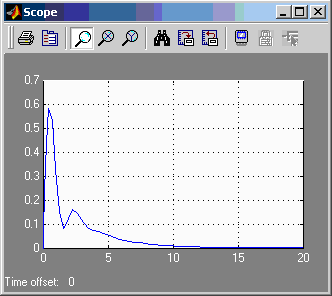
Система работает без ошибки. Отработав возмущающее воздействие, система вновь устанавливается в 0.

Охватить интегратор (), входящий в структурную схему САУ (рисунок 3), местной единичной отрицательной обратной связью.

Интератор, охваченный ОС

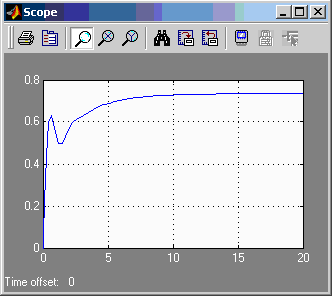
Система функционирует с ошибкой.

Система не устанавливается в 0.

ε_ст=0.75

Реакция САУ на ступенчатое задающее воздействие g(t)=1; f(t)=0

Переходные функции САУ

Интегратор не охвачен ОС

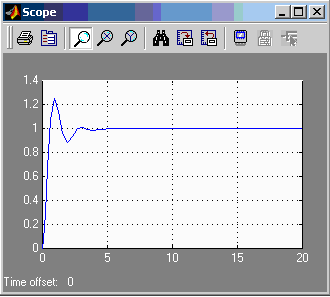
Система астатическая

h(t)=1, ε_ст=0

Интегратор охвачен ОС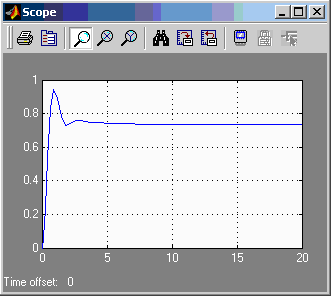

САУ - статическая

h(t)=0.75, ε_ст=0.25

g(t) ε(t) f(t) x(t)

Рис. 3

Найти передаточные функции САУ рис. 3 по ошибке управления и по отношению к возмущающему воздействию . На основании этих выражений сделать вывод о порядке астатизма данной системы.

где - полиномы, а - порядок астатизма,=1

Точность САУ по отношению к возмущающему воздействию f(t) можно оценить, используя соответствующую передаточную функцию

Порядок астатизма системы по отношению к возмущению определяется числом интегрирующих звеньев, расположенных в структурной схеме до точки приложения возмущения и не охваченных местными обратными связями.

Порядок астатизма системы по отношению к возмущению равен 1.

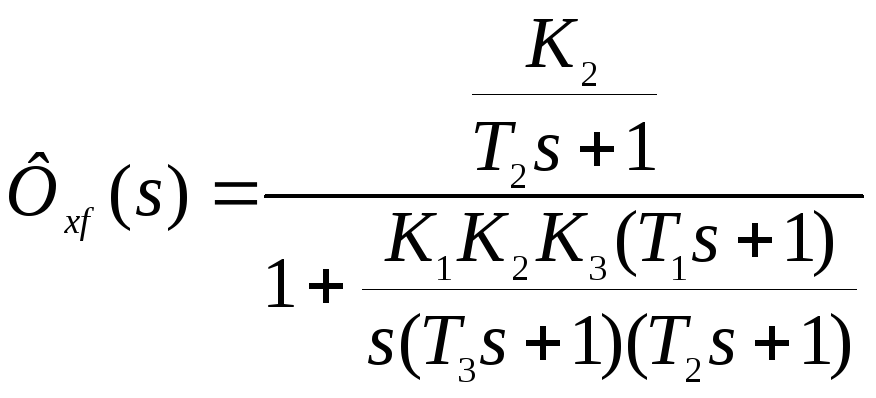
3. Выводы

В лабораторной работе были изучены критерии устойчивости Гурвица для линейных систем. С помощью этих критериев были исследованы на устойчивость САУ 2-го и 3-го порядков (с использованием автоматизированных средств моделирования на ПК – MATLAB). Были исследованы факторы, влияющие на точность линейных САУ.

10