
ТАУ. Методическое пособие
.pdf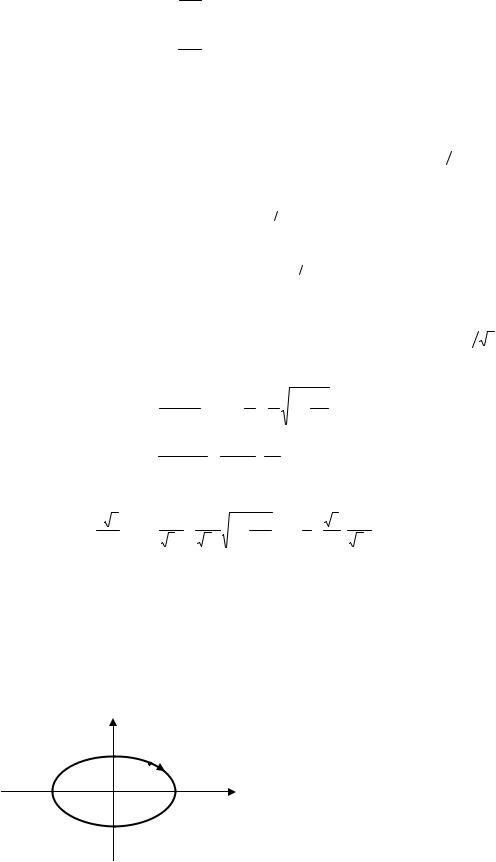
2π |
|
a ( A) = π1A ∫F(Asin ϕ) sin ϕdϕ; |
|
0 |
|
2π |
|
b ( A) = π1A ∫F(Asin ϕ) cos ϕdϕ . |
|
0 |
|
где ϕ = ωt , F(y) – статическая характеристика нелинейного звена. |
|
В алгебраической форме эквивалентная |
АФХ нелинейного элемента имеет вид |
J (A) = a(A) +i b(A) . |
|
Так как статическая характеристика x = F( y) |
симметрична относительно π 2 , то формулы |
для вычисления коэффициентов гармонической линеаризации в нашей задаче преобразуются к виду
|
4 |
|
ϕ |
|
|
|
|
|
4 |
|
π 2 |
|
|
|
|
|
|
|
||
a( A) = |
|
∫1 A tg 60o sin 2 |
ϕ dϕ+ |
|
∫c tg 60o sin ϕ dϕ; |
|
|
|||||||||||||
π A |
π A |
|
|
|||||||||||||||||
|
0 |
|
|
|
|
|
ϕ |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
4 |
|
ϕ |
|
|
|
|
|
|
|
|
4 |
π 2 |
|
|
|
|
|
|
|
b ( A) = |
|
∫1 A tg 60o sin ϕ cos ϕ dϕ+ |
∫c tg 60o cos ϕ dϕ . |
|
|
|||||||||||||||
π A |
π A |
|
|
|||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
ϕ |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
Проводя вычисления по приведенным формулам и подставляя sin ϕ = |
c |
, c = 2 3 получа- |
||||||||||||||||||
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
A |
|
ем следующие значения коэффициентов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
2tg 60 |
o |
|
|
|
c |
|
|
c |
|
|
c |
2 |
|
|
|
|
|
|
a (A) = |
|
|
arcsin |
+ |
|
|
1− |
|
|
; |
|
|
||||||
|
|
π |
|
|
A |
|
A |
|
A2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b ( A) = |
2 tg 60o c |
+ |
tg 60o 4 c |
− |
|
|
|
|
|
|
|
|||||||
|
|
πA |
|
|
π |
|
|
A |
1 . |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Эквивалентная АФХ нелинейного элемента запишется в виде:
|
2 3 |
|
2 |
|
2 |
|
4 |
|
|
4 |
|
3 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|||||||||
J(A) = |
|
arcsin |
|
+ |
|
1− |
2 |
|
+i |
|
+ |
|
|
|
|
|
π |
|
|
π |
π |
|
3A |
−1 . |
|||||||||
|
|
3A 3A |
3A |
|
|
|
|
|
|
|||||||
Задача 3. Нарисовать (качественно) переходный процесс, соответствующий фазовой траектории (рис. 16).
Для решения этой задачи надо познакомиться с фазовыми портретами линейных систем второго порядка. Эти фазовые портреты классифицируются по корням характеристического уравнения. Возможны шесть различных вариантов. Между фазовым портретом и переходным процессом системы существует взаимная связь, т.е. по фазовому портрету (фазовой траектории) можно качественно изобразить переходной процесс и, наоборот, по переходному процессу изобразить качественно ход фазовой траектории.
x
x
Рис. 16 Фазовая траектория: предельный цикл
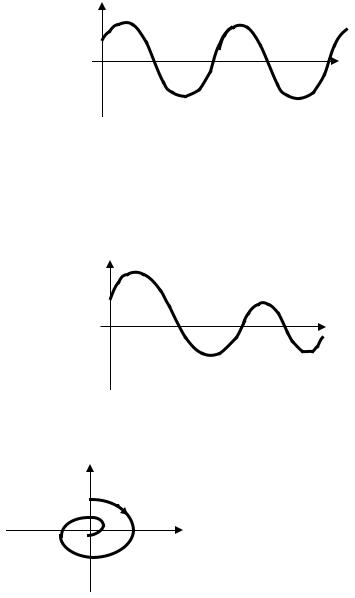
Заданной фазовой траекторией является замкнутая кривая, которая соответствует случаю, когда характеристическое уравнение имеет чисто мнимые корни, ее называют "центр". В этом случае система находится на границе устойчивости и переходной процесс представляет собой незатухающие колебания, изображенные на рис. 17.
x
t
Рис. 17 Незатухающий переходной процесс
Задача 4. Нарисовать (качественно) фазовую траекторию, соответствующую переходному процессу (рис. 18).
x
t
Рис. 18 Затухающий колебательный переходной процесс
x |
Задача является обратной задаче 3. Затухающий колеба- |
|||
|
тельный переходной процесс соответствует случаю, когда |
|||
|
корни характеристического уравнения – комплексно- |
|||
x |
сопряженные с отрицательной вещественной частью, что сви- |
|||
детельствует о том, что система устойчива. Этому случаю со- |
||||
|
ответствует фазовая траектория, получившая название "ус- |
|||
|
тойчивый фокус" (рис. 19). |
|||
|
Задача 5. Построить методом изоклин фазовый портрет |
|||
Рис. 19 Фазовая траектория – |
||||
для системы, уравнение движение которой имеет вид |
||||
"устойчивый фокус" |
||||
|
|
|
||
|
x |
′′ |
′ |
|
|
||||
|
|
+ x x +4x = 2 . |
||
При построении фазового портрета методом изоклин необходимо заданное дифференциальное уравнение второго порядка свести к системе двух уравнений дифференциальных уравнений первого порядка. В результате проведения этой математической процедуры получаем следующую систему двух дифференциальных уравнений первого порядка:
x′ = y;
y′ = 2 − yx −4x.
Для записи уравнения фазовой траектории в полученной системе дифференциальных уравнений надо избавиться от времени, для чего второе уравнение делится на первое, что и дает возможность записать дифференциальное уравнение фазовой траектории
d y |
= |
2 − yx −4x |
. |
d x |
|
y |
|
Метод изоклин построения фазового портрета дает качественную картину хода фазовых траекторий. Прежде всего на фазовой плоскости строится поле изоклин. Изоклина – кривая равного наклона, ее уравнением является уравнение
d y |
= |
2 − yx −4x |
= C = const , |
|
d x |
y |
|||
|
|
где C – задаваемая константа.
Решим полученное дифференциальное уравнение изоклины относительно y и выразим его через x. В результате получим
y = 2C−+4xx .
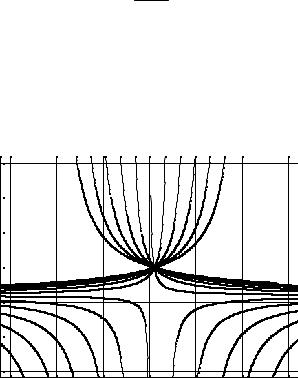
Задаваясь значениями С от –10 до 10 с шагом два, строим семейство изоклин (рис. 20). Фазовая траектория пересекает соответствующую изоклину под углом arctg C. Произвольно задается начальная точка для начала фазовой траектории. Далее, нанося на каждой изоклине стрелки под углом arctg C, определяем качественный ход фазовой траектории, так как стрелки определяют направление касательной к фазовой траектории. Таким образом
строится семейство фазовых траекторий, составляющих фазовый портрет.
15
10 








5 




0 

-5
-10 


-15
-15 |
-10 |
-5 |
0 |
5 |
10 |
15 |
Рис. 20 Фазовый портрет системы, построенный методом изоклин
Задача 6. Определить возможные состояния равновесия системы и исследовать их устойчивость первым методом Ляпунова, если она описывается системой уравнений
d x = P(x, y) = −x + xy;d t
d y = Q(x, y) = −y + y2 .d t
Первый метод Ляпунова исследования устойчивости нелинейных систем дает ответ об устойчивости состояния равновесия, которое прежде всего и необходимо определить. В состоянии равновесия производные равны нулю, поэтому, приравнивая нулю производные, получим систему нелинейных алгебраических уравнений для определения состояний равновесия. Решим эту систему уравнений:
d x = P(x, y) = −x + xy = 0;d t
d y = Q(x, y) = −y + y2 = 0.
d t
Система имеет два решения: x1 = 0, y1 = 0 и x2 = 0, y2 = 1. Найденные корни – это точки равновесия исходной системы.
Для применения первого метода Ляпунова необходимо исходную нелинейную систему линеаризовать методом разложения в ряд Тейлора в окрестности точек состояний равновесия. В результате линеаризации получим следующую линейную систему дифференциальных уравнений:

dxdt = a1x +a2 y; dydt = b1x +b2 y,
где a |
= |
∂P |
|
, a |
|
= |
∂P |
|
, b |
= |
∂Q |
|
x1, y1 |
, b |
2 |
= |
∂Q |
|
. |
|
|
|
|
|
|||||||||||||||
1 |
|
∂ x |
x1, y1 |
|
2 |
|
∂ y |
x1, y1 |
1 |
|
∂ x |
|
|
|
∂ y |
|
x1, y1 |
Проведем линеаризацию исходной системы в окрестности точки (0, 0), для этого рассчитаем коэффициенты линеаризованного уравнения:
a |
= |
∂ P |
|
|
x1, y1 |
= −1 ; |
|
a |
2 |
= ∂ P |
|
= 0 ; |
||||||
|
|
|
|
|||||||||||||||
1 |
|
∂ x |
|
|
|
|
|
|
∂ y |
|
x1, y1 |
|||||||
b |
= |
∂Q |
|
|
|
= 0 ; |
b |
2 |
= |
|
∂Q |
|
|
|
|
= −1 . |
||
|
|
|
||||||||||||||||
∂ x |
|
|
x1, y1 |
|
∂ y |
|
|
|
||||||||||
1 |
|
|
|
|
|
|
|
|
x1, y1 |
|||||||||
Линеаризованная система дифференциальных уравнений в точке (0, 0) имеет вид
d x = −x;
d t
d y = −y.d t
Первый метод Ляпунова гласит: если линеаризованная система первого приближения устойчива, то и исходная нелинейная система устойчива; если линеаризованная система первого приближения неустойчива, то и исходная нелинейная система неустойчива; если линеаризованная система первого приближения нейтральна, то относительно исходной нелинейной системы сказать ничего нельзя, необходимо исследовать систему второго приближения.
Исследуем на устойчивость полученную линейную систему любым известным методом исследования устойчивости линейных систем. Проще всего в данном случае рассчитать корни характеристического уравнения и применить необходимое и достаточно условие исследования устойчивости. Для этого составим дискриминант
D(λ) = |
|
1+λ 0 |
|
= 0 . |
|
|
|
||||
|
|
0 |
1+λ |
|
|
Характеристическое уравнение будет – (λ+1)2 = 0 , его корни: λ1 = λ2 = −1 . Корни действи-
тельные отрицательные, а это говорит том, что система в окрестности точки (0, 0) является устойчивой и, кроме того, состояние равновесия представляет собой устойчивый узел.
Исследуем второе состояние равновесия. Определим коэффициенты линеаризованного уравнения в окрестности точки (0, 1).
a |
= |
∂ P |
|
|
|
= 0 ; |
a |
2 |
= |
∂ P |
|
|
= 0 ; |
|
|
|
|
|
|||||||||||
∂ x |
|
x2 , y2 |
∂ y |
|||||||||||
1 |
|
|
|
|
|
|
|
x2 , y2 |
||||||
b |
= |
∂Q |
|
|
|
= 0 ; |
b |
2 |
= |
∂Q |
|
|
|
=1 . |
|
|
|
||||||||||||
∂ x |
|
|
x2 , y2 |
∂ y |
||||||||||
1 |
|
|
|
|
|
|
|
|
x2 , y2 |
|||||
Линеаризованная система в точке (0, 1) имеет вид
d x = 0;
d t
d y = y.d t
Исследуем на устойчивость, полученную линеаризованную систему. Запишем ее дискриминант
D(λ) = |
|
λ |
0 |
|
= 0 . |
|
|
||||
|
|
0 |
λ−1 |
|
|
Характеристическое уравнение имеет вид – (λ−1) λ = 0 , его корни: λ1 = 0 ; λ2 =1.
Один из корней положительный, следовательно, система в окрестности точки (0, 1) является неустойчивой. Состояние равновесия – неустойчивый узел.
Список рекомендуемой литературы
1.Лазарева Т.Я., Мартемьянов Ю.Ф. Основы теории автоматического управления: Учеб. пособие. Тамбов: Изд-во Тамб. гос. техн. ун-та, 2004. 352 с.
2.Лазарева Т.Я., Мартемьянов Ю.Ф. Линейные системы автоматического регулирования: Учеб. пособие. Тамбов: Изд-во Тамб. гос. техн. ун-та, 2001. 264 с.
3.Лазарева Т.Я. Нелинейные системы автоматического управления: Учеб. пособие. Тамбов: Изд-во Тамб. гос. техн. ун-та, 1996. 84 с.
4.Лазарева Т.Я. Системы автоматического управления со случайными воздействиями: Учеб. пособие. Тамбов: Изд-во Тамб. гос. техн. ун-та, 1999. 64 с.
5.Топчеев Ю.И., Цыпляков А.П. Задачник по теории автоматического регулирования: Учеб. пособие. М.: Машиностроение, 1977.
6.Теория автоматического управления / Под ред. А.А. Воронова. М.: Высшая школа, 1986. 367 с.
7.Автоматическое управление в химической промышленности: Учебник / Под ред. Е.Г. Дудникова. М.:
Химия, 1987. 368 с.
Оглавление |
|
ВВЕДЕНИЕ …………………………………………………………….. |
3 |
Тема 1Основные сведения о системах автоматического регулирова- |
|
ния ……………………………………………………. |
3 |
Тема 2МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ СИСТЕМ АВТОМА- |
|
ТИЧЕСКОГО УПРАВЛЕНИЯ …………………………….. |
4 |
Тема 3 ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ СИС- |
|
ТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ |
|
………………………... |
6 |
Тема 4ОСНОВЫ СТРУКТУРНОГО МЕТОДА ИССЛЕДОВАНИЯ- |
|
СИСТЕМЫ ……………………………………………………………... |
7 |
Тема 5УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ |
|
…………………………. |
9 |
Тема 6ОБЕСПЕЧЕНИЕ УСТОЙЧИВОСТИ |
|
…………………………………. |
10 |
Тема 7ИССЛЕДОВАНИЕ КАЧЕСТВА ПРОЦЕССА РЕГУЛИРО- |
|
ВАНИЯ .. |
11 |
Тема 8СИНТЕЗ ОДНОКОНТУРНЫХ АВТОМАТИЧЕСКИХ СИС- |
|
ТЕМ РЕГУЛИРОВАНИЯ |
|
……………………………………………………. |
12 |
Тема 9СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ СИСТЕМЫ. СХЕМ- |
|
НЫЕ МЕТОДЫ ПОВЫШЕНИЯ КАЧЕСТВА ПЕРЕХОДНЫХ |
|
ПРОЦЕССОВ ……………………………………….. |
14 |
Тема 10ХАРАКТЕРИСТИКА НЕЛИНЕЙНЫХ СИСТЕМ АВТО- |
|
МАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ………………………... |
15 |
Тема 11УСТОЙЧИВОСТЬ И КАЧЕСТВО НЕЛИНЕЙНЫХ СИС- |
|
ТЕМ …….. |
17 |
Тема 12СЛУЧАЙНЫЕ ПРОЦЕССЫ В СИСТЕМАХ АВТОМАТИ- |
|
ЧЕСКОГО УПРАВЛЕНИЯ …………………………….. |
18 |
ЗАДАНИЯ ……………………………………………………………… |
20 |
Контрольная работа 1 ……………………………………………. |
20 |
Контрольная работа 2 ……………………………………………. |
27 |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ………………………………………. |
32 |
Список рекомендуемой литературы …………………….. |
55 |
