Добавил:

Studfiles2 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уфимский Государственный Авиационный Технический Университет

Предмет:

Теория автоматического управления

Файл:

ТАУ. Методическое пособие

.pdf

Скачиваний:

118

Добавлен:

02.05.2014

Размер:

642.4 Кб

Скачать

☆

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

5Что такое автоколебания?

6Изобразите фазовые портреты нелинейной системы, иллюстрирующие режимы мягкого и жесткого возбуждения автоколебаний.

Литература: [1, 3].

Т е м а 11 УСТОЙЧИВОСТЬ И КАЧЕСТВО НЕЛИНЕЙНЫХ СИСТЕМ

Программа

Устойчивость состояния равновесия и автоколебаний в нелинейных системах. Устойчивость по А.М. Ляпунову. Асимптотическая устойчивость. Первый и второй методы А.М. Ляпунова.

Абсолютная устойчивость. Метод В.П. Попова. Приближенные методы исследования устойчивости и параметров автоколебаний. Метод гармонического баланса.

Качество переходных процессов в нелинейных системах. Улучшение динамических свойств систем при помощи нелинейных связей.

Методические указания

Сложные вопросы устойчивости процессов регулирования нелинейной системы можно наглядно представить, используя, как и в линейных системах, понятие фазового пространства. Здесь необходимо обратить внимание на различные виды устойчивости и их геометрическую интерпретацию в фазовом пространстве. В частности, необходимо знать понятия орбитальной устойчивости; устойчивости нелинейной системы "в малом", "в большом", "в целом"; устойчивости по А.М. Ляпунову; асимптотической устойчивости.

Для исследования устойчивости нелинейных систем используются два метода А.М. Ляпунова. Первый из них позволяет исследовать устойчивость системы "в малом", а второй – "в большом". Необходимо уметь формулировать теоремы Ляпунова, применять их к решению задач, знать основные проблемы практического использования второго метода – это выбор функции Ляпунова. Необходимо познакомиться с рекомендации по составлению функции Ляпунова для конкретных систем.

Для исследования абсолютной устойчивости используется метод В.П. Попова, относящийся к группе частотных методов. Студенту рекомендуется познакомиться с функцией Попова, знать геометрическую интерпретацию метода.

Изучение устойчивости нелинейных систем следует закончить приближенными методами исследования устойчивости автоколебаний. Здесь необходимо отметить использование такого метода, как метод гармонического баланса, основанного на применении частотных характеристик, полученных при гармонической линеаризации нелинейностей.

В заключение темы студент знакомится с вопросами качества переходных процессов в нелинейных систе-

мах.

Вопросы для самопроверки

1Как вы понимаете устойчивость состояния равновесия и устойчивость автоколебаний?

2Дайте сравнительную характеристику различных видов устойчивости.

3Прокомментируйте использование первого и второго методов устойчивости А.М. Ляпунова.

4Покажите связь критерия абсолютной устойчивости Попова с критерием Найквиста.

5Как определить устойчивость автоколебаний методом гармонического баланса?

Литература: [3, 4, 6].

Т е м а 12

СЛУЧАЙНЫЕ ПРОЦЕССЫ В СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Программа

Элементы теории вероятности. Случайные величины, законы распределения и вероятностные характеристики случайной величины: математическое ожидание, дисперсия, центрированная случайная величина. Понятие об оценках, требования к оценкам.

Случайные стационарные процессы, свойство эргодичности, марковские процессы. Характеристики случайных процессов: корреляционная функция, спектральная плотность.

Преобразование случайных сигналов линейными системами. Характеристики выходного сигнала. Связь между корреляционными функциями, спектральными плотностями входного и выходного сигналов.

Основные задачи анализа и синтеза систем при случайных воздействиях. Оптимальная ширина полосы пропускания идеального полосового фильтра. Анализ и синтез систем по минимуму среднеквадратичной погрешности. Общая задача упреждения и фильтрации. Уравнение Винера-Хопфа и методы его решения.

Методические указания

Студентам заочного отделения тему "Случайные процессы в системах автоматического управления" рекомендуется изучить обзорно, познакомившись с основными понятиями, используемыми при описании случайных величин, случайных стационарных процессов. Необходимо изучить и уметь составлять корреляционную функцию и спектральную плотность случайного процесса, понять суть расчета систем автоматического управления со случайными воздействиями, знать уравнение Винера-Хопфа.

Вопросы для самопроверки

1Назовите основные характеристики случайной величины.

2Какой случайный процесс называется случайным стационарным процессом?

3Что такое свойство эргодичности?

4Как экспериментально определить корреляционную функцию случайного процесса?

5В чем заключается расчет системы автоматического управления со случайными воздействиями?

6Какие методы определения спектральной плотности Вам известны? Какой из них наиболее эффективен

сВашей точки зрения?

7Какие методы решения уравнения Винера-Хопфа Вы знаете?

Литература: [2, 3, 6].

ЗАДАНИЯ

Контрольная работа 1

Задача 1

Найти оригиналы по заданным изображениям (табл. 1).

Таблица 1

№ вари-

F1(s)

F2(s)

анта

2e−s

s + 6

(s +1)(s2 + 3s + 2)(s2 + s +1)

s +1

5e−3s

5s +8

s2 ( p + 2)(s2 + 5s +5)

s2 + 4

e−2s

s + 6

(s + 2)(s2 + 3s)(s2 + 4s + 5)

4s +2

3e−2s

2s +8

s(s2 + 2s)(s2 + 4s + 5)

6s +1

2e−3s

(s + 4)(s2 + 6s +8)(s2 + 4s + 29)

4e−3s

2s +10

s4 (s2 + 6s +10)

3s +1

5e−2s

(s +1)(s2 + 9s +14)(s2 + s +1)

7e−2s

2s +5

s3 (s2 +5s +13)

(s + 3)3

3e−2s

s + 2

(s + 5)(s2 + 6s − 4)(s2 + s +10)

e−4s

12s +8

s3 (s +1)(s2 + s +1)

Задача 2

С помощью преобразования Лапласа решить дифференциальное уравнение с заданными начальными условиями (табл. 2).

Таблица 2

№ вари-

Уравнение

Начальные условия

анта

0	y" + 4y' + 3y = 2e–t cos(t)	y(0) = 0; y'(0) = 1
1	y" + y' + 5y = 2sin(t)	y(0) = 0; y'(0) = 0
2	y" – 2y' + 5y = 2sin(2t)	y(0) = 0; y'(0) = 1
3	y" – y' + 2y = 3e2tcos(2t)	y(0) = 0; y'(0) = 1
	t
4	y" + 6y' + 13y = ∫et dt	y(0) = 0; y'(0) = 1
	0
5	y" + y' – 5y = 2e2tsin(t)	y(0) = 0; y'(0) = 1
6	y" + 2y' + y = et	y(0) = 1; y'(0) = 0
7	yIV – y" = e–t cos(t)	y(0) = 0; y'(0) = –1; y"(0) = y"'(0) = 0
8	y"' – y" = e2t	y(0) = 1 ; y'(0) = y"(0)
9	y" – y' = te2t	y(0) = 0; y'(0) = 0

Задача 3

По известной кривой разгона и весовой функции линейного элемента (табл. 3) найти: 1) реакцию на входной сигнал x (t) ; 2) весовую функцию или кривую разгона соответственно; 3) передаточную функцию элемента.

Таблица 3

№ варианта	h (t)	ω(t)	x (t)

0	1 −e−3t	e−t	t 2
1	4e−2t	t e−2t	t
2	t 2 +t	1−e−t	1−e−t
3	1−e−2t	4e−2t	1−e−2t
4	−1−e−2t +t	t e−t	t 2 −1
5	1 −e−t cos t	8t e− t 2	t −1
6	t 2 +1	e−2t	sin 3t
7	2t 2	2 −t e−t	1 − e−2t sin t
8	2 (1 −e−3t )	t e−2t	2t 2 +t
9	1 −e−2t sin 3t	5e−3t	t +1

Задача 4

По известной передаточной функции элемента W(s) найти его кривую разгона, весовую функцию, ампли- тудно-частотную, фазо-частотную, амплитудно-фазовую характеристики. Построить графики. Записать дифференциальное уравнение элемента, связывающее выходную координату и входную координату (табл. 4).

Таблица 4

№ варианта

Передаточная функ-

№ варианта

Передаточная функция

ция W(s)

W(s)

2s +1

s +1

(s +1)(s

+2)

(3s +1)(2s

+1)

4s +

2s +3

(2s +1)(s + 2)

(3s +1)(4s

+3)

2s + 3

5s + 4

(2s +1)(s + 3)

(2s −3)(4s +3)

2s + 5

3s + 2

(3s + 2)(2s + 4)

(2s +1)(s + 2)

3s +

s +2

(3s + 4)(s +1)

(2s +1)(3s

+2)

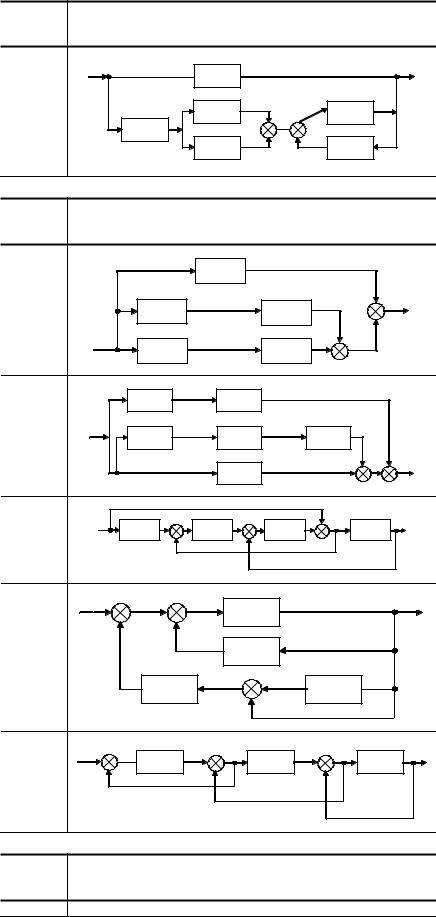
Задача 5

Вывести передаточную функцию для заданной структурной схемы (табл. 5).

№ вари-					Структурная схема
анта					Структурная схема
анта
		х			W1(s)			y
					W1(s)
0					W3(s)		W5(s)
				W2(s)
					W4(s)		W6(s)
№ вари-					Структурная схема
анта					Структурная схема
анта
					W1(s)
1				W2(s)		W3(s)		y
1				W2(s)		W3(s)
			х	W4(s)		W5(s)
				W4(s)		W5(s)
				W1(s)		W2(s)
2		х		W3(s)		W4(s)	W5(s)
2				W3(s)		W4(s)	W5(s)
						W6(s)		y
						W6(s)
			х	W1(s)	W2(s)	W3(s)	W5(s)	y
			х
3
3
	х					W1(s)		y
	х

4						W2(s)
4
				W3(s)			W4(s)
	х			W1(s)		W2(s)	W3(s)	y
	х

5
№ вари-					Структурная схема
анта					Структурная схема
анта
6

Таблица 5

Продолжение табл. 5

	х				y
	х		W1(s)	W2(s)	W3(s)
			W1(s)	W2(s)	W3(s)
				W4(s)
				W5(s)
				W2(s)
7		х	W1(s)	W4(s)	y
7			W1(s)	W4(s)
				W3(s)
	х		W1(s)	W2(s)	y
			W1(s)	W2(s)
8
			W1(s)
				W3(s)
9		х	W2(s)	W4(s)	y
			W2(s)	W4(s)

				W5(s)
				W6(s)
Задача 6

Исследовать на устойчивость систему автоматического регулирования, схема которой приведена на рис. 1 (табл. 6):

1)с помощью критерия Рауса–Гурвица;

2)с помощью критерия Михайлова.

	x	Wp(s)	Wоб(s)	y
		Рис. 1
				Таблица 6
№ варианта	Wp(s)	Wоб(s)
0	4 +3s	3s +1
0	s	3s3 + 2s2 + s +1
	s	3s3 + 2s2 + s +1
1	1+2s	3
1	1+2s	2s4 + s3 + 2s2 + 3s + 4
		2s4 + s3 + 2s2 + 3s + 4
2	3 + s	2
2	s	3s3 + s2 + s +1
	s	3s3 + s2 + s +1
3	3s + 2	4
3	3s + 2	4s4 + 3s3 + 2s2 + 2
		4s4 + 3s3 + 2s2 + 2

2s2 +1

3s3 + 3s2 + 2s +3

s2 +5

3s4 + s3 +5s2 + s +1

3s +1

3s2 + s +1

s4 + 2s3 + 2s2 + s + 5

s +2

s3 +2s2 + s +4

4s +1

s4 + 2s3 + 7s2 + s + 6

3s +2

2s + 3

s3 + 2s2 + s +10

Задача 7

Исследовать на устойчивость с помощью критерия Найквиста систему автоматического регулирования,

схема которой приведена на рис. 2 (табл. 7).

Wp(s)

Wоб(s)

e–2s

Рис. 2

Таблица 7

№ варианта

Wр(s)

W (s)

об

3 +

3s +1

6 +

2s +1

4 +

s +1

7 +

s +1

6 +

s + 2

5 +

s +8

10 + 1

2s +3

4 +

3s +1

5s +1

3 +

2s +1

Контрольная работа 2

Задача 1

Уравнение статики объекта имеет вид, представленный в табл. 8. Линеаризовать уравнение в окрестности точки х0 =1, y0 = y(х0 ) = y(1) . Построить статическую характеристику линеаризованного объекта и сравнить с

исходной.

Таблица 8

№ варианта	Статическая характери-	№ варианта	Статическая характери-
	стика		стика
0	y = 1	1	y3 = х
	х
2	y = ln(х +1)	3	y = e х
4	y = х4	5	y =х2 +1
6	y = х5	7	y = 1
			х
8	y 2 = х	9	y = 3х2 ln х
Задача 2

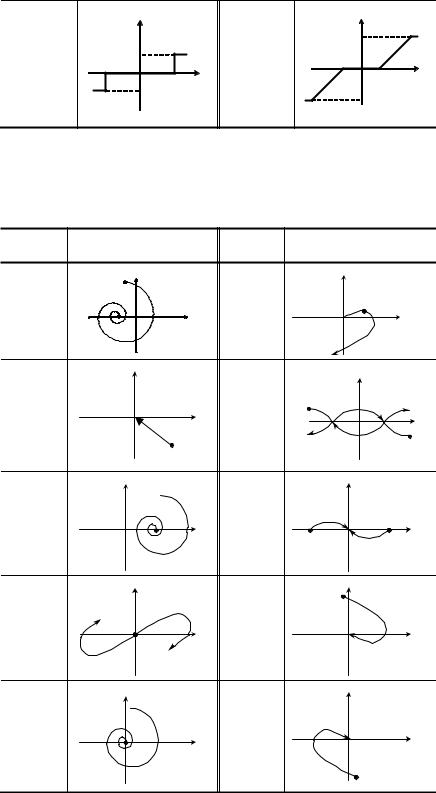
На вход нелинейного элемента подаются гармонические колебания. Нарисовать вынужденные колебания на выходе нелинейного элемента. Вывести формулу эквивалентной передаточной функции нелинейного элемента с помощью метода гармонической линеаризации. Статическая характеристика нелинейного элемента приведена в табл. 9.

№ варианта	Статическая характери-		№ варианта	Статическая характери-
	стика			стика
	x			x
0	1		1	1
0			1	–1
	–1	y		–1 1		y
№ варианта	Статическая характери-		№ варианта	Статическая характери-
	стика			стика
	x			x
2	1		3	1
2	45°	y	3	–1	45°
	–1	y		–1 1		y
	–1			–1 1		y
	x			x
	1			1
4	–1		5	1
4	–1		5	–2 –1
	1	y		–1 1	2	y
	–1
	x			x
				2
6	–1	45°	7			y
	–1	45°				y
	1	y
				–2

Таблица 9

Продолжение табл. 9

	x			x
				2
8	1		9	–1	45°
8	–2		9	–1	45°
	–1	2	y	1	y
		2	y
				–2
				–2

Задача 3

Нарисовать (качественно) переходные процессы, соответствующие фазовым траекториям, указанным в табл. 10.

Таблица 10

№ вари-	Фазовая траектория			№ вари-	Фазовая траектория
анта	Фазовая траектория			анта	Фазовая траектория
анта				анта
	M 0	y				y
	M 0	y
0	–1			1		M 0
0			x	1		x
			x			x
		y				y
						y
2				3	M 0
2			x	3		x
			x			x
			M 0			M 0
			M 0
		y				y
4			1	5		M 0
			x		M 0	x
		y				y
						M 0
6		M 0	x	7		x
		M 0	x			x
		y				y
8			x	9		x
			x			x
						M 0

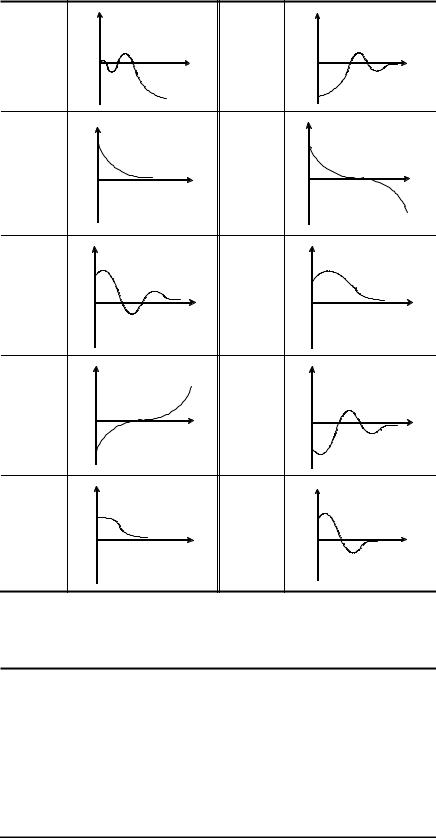
Задача 4

Нарисовать (качественно) фазовые траектории, соответствующие переходным процессам, указанным в табл. 11.

Таблица 11

№ вари-	Фазовая траектория	№ вари-	Фазовая траектория
анта	Фазовая траектория	анта	Фазовая траектория
анта		анта

y	y
0	1
t	t
y	y
y
2	3
t	t
y	y
4	5
t	t
y	y
6	7
t	t
y	y
8	9
t	t
Задача 5

Построить методом изоклин фазовый портрет для системы, уравнение движения которой представлено в табл. 12.

Таблица 12

№ вари-

Уравнение

анта

′′

′

+ х =1

х х

′′

+ х

′

+ х

х х

′′

′

+ х =1

х х

′′

′

+ 2х = 3

х х

х′′х+0,5х+ х2 = 3

№ вари-			Уравнение
анта


1	х′′х2 + х′+0,5х = 3
3	′′		′	2	+ х =1
	х х+ х х
5	х′′+ х′+ х2 = 2
7	х	′′	′
			+ х х+3х = 4
9	х′′х2 + х′+ х = 2

Задача 6

Определить возможные состояния равновесия системы и исследовать их устойчивость первым методом

Ляпунова, если она описывается системой уравнений:				dх	= Р(х, y) ;	dy	= Q(х, y) (табл. 13).
Ляпунова, если она описывается системой уравнений:				dt	= Р(х, y) ;	dt	= Q(х, y) (табл. 13).
				dt		dt		Таблица 13
								Таблица 13

№ вари-	Система уравнений	№ вари-	Система уравнений
анта	Система уравнений	анта	Система уравнений
анта		анта
0	P(х, y) = 0,5y2 − y + х	1			P(х, y) = y

		Q(х, y) = хy +1

	2	P(х, y) = y − х+1
	2	Q(х, y) = y − х2 + 2х
		Q(х, y) = y − х2 + 2х
	4	P(х, y) = 0,5х+ y
	4	Q(х, y) = 2хy +1
		Q(х, y) = 2хy +1

	6	P(х, y) = 2х2 + y +1
	6	Q(х, y) = y − х2 +2х
		Q(х, y) = y − х2 +2х
	8	P(х, y) = y2 х+1
	8	Q(х, y) = х+0,5y
		Q(х, y) = х+0,5y

		Q(х, y) = y − х2 + 2х
	3	P(х, y) = х+ y
	3	Q(х, y) = 2х2 + y −1
		Q(х, y) = 2х2 + y −1
	5	P(х, y) = y − х2 + 2х
	5	Q(х, y) = хy +1
		Q(х, y) = хy +1

	7	P(х, y) = 2х2 y +1
	7	Q(х, y) = х+ y
		Q(х, y) = х+ y

	9	P(х, y) = y 2 − y + 2х
	9	Q(х, y) = 3х2 + y
		Q(х, y) = 3х2 + y

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ Контрольная работа 1

Задача 1. Найти оригиналы по заданным изображениям, используя преобразование Лапласа:

F (s) =	4 e−s		,	F	(s) =	3s +	7		.

1	(s +3)	2		2		s3 (s2 + 6s		+13)

По таблице преобразования Лапласа и свойствам преобразования Лапласа найдем

F1 (t) = 4I (t −1)te−3(t−1) ,

где I – единичная функция.

Для определения преобразования Лапласа от дроби F2 (s) необходимо эту правильную рациональную

дробь представить в виде суммы простейших дробей, которые определяются в соответствии с корнями характеристического уравнения и по которым преобразование Лапласа можно взять, используя таблицы преобразования; рассматриваемая дробь имеет три нулевых корня и пару комплексно-сопряженных корней, поэтому она разлагается на простейшие дроби следующим образом:

F (s) =

3s + 7

Ds + E

s3 (s

2 + 6s +13)

s s2 s3

(s2 + 6s +13)

As2

(s 2 + 6s +13)

+ Bsp(s 2 + 6s +13) + C(s 2 + 6s +13) +

(Ds + E)s3

s3 (s 2 + 6s +13)

В результате разложения получена сумма простейших дробей, коэффициенты которых определяются методом неопределенных коэффициентов, для чего рассматривается равенство двух дробей. Две правильные рациональные дроби равны между собой, если равны их числители и знаменатели. Так как знаменатели равны, то, следовательно, необходимо приравнять друг к другу и числители. Приравняв в числителях коэффициенты при одинаковых степенях параметра s , получим систему алгебраических уравнений для определения неизвестных коэффициентов:

A + D = 0;

6A + B + E = 0;13A +6B +C = 0;

13B +6C = 3;

13C = 7.

Решение системы дает следующие корни:

A = −	73	;	B = −	3	;	C =		7	;	D =	73	;	E =	477	.
	2197			169			13				2197			2197

Таким образом, исходная дробь записывается в виде

( p) =

−

73s + 477

13 s3

169 s2

2197 s

2197 s2 + 6s +13

В соответствии с таблицами преобразований Лапласа оригинал имеет вид

F2 (t) = 267 t 2 − 1693 t − 219773 + 219773 + e−3t cos 2t + 2197129 e−3t sin 2t.

Задача 2. С помощью преобразования Лапласа решить дифференциальное уравнение с заданными начальными условиями:

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

Соседние файлы в предмете Теория автоматического управления

#
02.05.20141.61 Mб38Синтез и анализ двухконтурной системы стабилизации скорости вращения антенны.doc
#
02.05.20145.48 Mб106Соломонцев Ю.М. Теория автоматического управления.pdf
#
02.05.201410.46 Mб251Сольницев Р. И. Автоматизация проектирования систем автоматического управления.doc
#
02.05.2014730.52 Кб156ТАУ в примерах и задачах [12].pdf
#
02.05.2014768.45 Кб117ТАУ в примерах и задачах [22].pdf
#
02.05.2014642.4 Кб118ТАУ. Методическое пособие.pdf
#
02.05.2014730.52 Кб141Теория автоматического управления в задачах и примерах [12].pdf
#
02.05.2014768.45 Кб219Теория автоматического управления в задачах и примерах [22].pdf
#
02.05.2014961.08 Кб86Туманов М.П. Теория линейных систем автоматического управления..pdf
#
02.05.2014961.08 Кб130Туманов М.П. Теория управления. Теория линейных систем автоматического управления.pdf
#
02.05.2014538.62 Кб232Шпора по ТАУ.doc