
- •1. Понятие тау как науки.
- •2. Основные понятия и определения теории управления.
- •3. Задачи теории автоматического управления.
- •4. Принципы построения сау.
- •5. Классификация систем автоматического управления.
- •6. Понятие о звене сау и его статической характеристике.
- •7. Типовые входные воздействия. Переходная и импульсная характеристики.
- •8. Методы описания динамических свойств звеньев и систем: модели "вход-выход", описание в пространстве состояний.
- •9. Понятие передаточной функции. Свойства преобразования Лапласа.
- •10. Понятие о частотных характеристиках.
- •11. Типовые динамические звенья (временные и частотные характеристики, передаточные функции).
- •12. Преобразование структурных схем сау. Связь структурных схем с графами.
- •13. Передаточные функции группы звеньев при последовательном, параллельном и встречно-параллельном соединении звеньев.
- •14. Передаточные функции замкнутой сау по управлению, по возмущению и по ошибке.
- •15. Понятие устойчивости сау.
- •16. Связь устойчивости с корнями характеристического уравнения сау. Теоремы Ляпунова.
- •17. Алгебраические критерии устойчивости(Рауса, Гурвица и т.Д)
- •18. Частотные критерии устойчивости:( Михайлова, Найквиста и т.Д)
- •19. Применение критерия Найквиста при наличии астатических и консервативных звеньев.
- •20. Влияние запаздывания на устойчивость сау.
- •21’. Построение областей устойчивости методом д-разбиения.
- •21’’. D-разбиение по одному параметру.
- •21''’. D-разбиение по 2 параметрам
- •22. Установившиеся режимы в сау и точность в установившемся режиме.
- •23. Методы построения переходных процессов в сау: классическийи операторный методы.
- •24. Метод построения переходных процессов в сау с помощью трапецеидальных вчх.
- •25. Временные показатели качества переходных процессов.
- •26. Частотные показатели качества процесса регулирования.
- •27. Интегральные показатели процесса регулирования.
- •28. Оценка качества переходных процессов по расположению корней. Диаграмма Вышнеградского.
- •29. Синтез сау по желаемой передаточной функции.
- •30. Синтез регулятора в пространстве состояний. Наблюдатель.
- •31. Синтез сау по логарифмическим частотным характеристикам.
- •32. Методы повышения точности работы сау.
- •34. Системы подчиненного регулирования. Путеводитель
12. Преобразование структурных схем сау. Связь структурных схем с графами.
Л
 юбую
САУ можно рассматривать как комбинацию
динамических звеньев. Изображение САУ
в виде совокупности динамических звеньев
с указателями связей между ними назыв.
структурной схемой.1)
звено с 1 входом и выходом
для него Y(p)=W(p)
*X(p)
2)
звено с 2-мя входами
юбую
САУ можно рассматривать как комбинацию
динамических звеньев. Изображение САУ
в виде совокупности динамических звеньев
с указателями связей между ними назыв.
структурной схемой.1)
звено с 1 входом и выходом
для него Y(p)=W(p)
*X(p)
2)
звено с 2-мя входами
д ля
негоY(p)=W1(p)*X1(p)+
W(p)*X2(p).
Его можно представить и в другом виде:
ля
негоY(p)=W1(p)*X1(p)+
W(p)*X2(p).
Его можно представить и в другом виде:

3) Узел х1=х2=х3
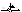
4) Сумматор y=x1±x2


или или
П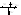

 равило
преобраз. структурных схем:
1)
перестановка однотипных элементов: а)
узлы с узлами, б) сумматоры с сумматорами,
в) звенья со звеньями:
равило
преобраз. структурных схем:
1)
перестановка однотипных элементов: а)
узлы с узлами, б) сумматоры с сумматорами,
в) звенья со звеньями:
= =


=
 2)
Перенос узла череззвено: а) с выхода на
вход б) со входа
2)
Перенос узла череззвено: а) с выхода на
вход б) со входа
на выход =


=
3
W1
Х1
Х3




 )
Перенос сумматора через звено: а) со
входа на выход б) с выхода на вход
=
)
Перенос сумматора через звено: а) со
входа на выход б) с выхода на вход
=
Х2




С
W(р)
х
у



П ример:
ример:

13. Передаточные функции группы звеньев при последовательном, параллельном и встречно-параллельном соединении звеньев.
1 )
Последовательное соед. Называется
соединение при котором выходной сигнал
предыдущего яв-ся входным для последующего.
)
Последовательное соед. Называется
соединение при котором выходной сигнал
предыдущего яв-ся входным для последующего.
Yi(p)=Wi*Xi(p), x=x1, x=x2, y=y3, y3=y. Y(p)= Y3(p)= W3(p)*X3(p)=Y2(p)*W3(p)=W2(p)*W3(p)* X2(p)=W2(p)*W3(p)*Y1(p)=W1(p)*W2(p)* W3(p) * X(p). Wэ(p)=Y(p)/X(p)=W1(p)*W2(p)*W3(p)=
Π ni=1Wi(p).
Вывод:
П.Ф. группы послед. соед. звеньев = произв.
передат. ф-ий отдельных звеньев. 2)
Параллельное соед. Назыв. соединение
при котором входной сигнал яв-ся общим
для всех звеньев, а выходной яв-ся суммой
всех выходных звеньев.
ni=1Wi(p).
Вывод:
П.Ф. группы послед. соед. звеньев = произв.
передат. ф-ий отдельных звеньев. 2)
Параллельное соед. Назыв. соединение
при котором входной сигнал яв-ся общим
для всех звеньев, а выходной яв-ся суммой
всех выходных звеньев.
Yi(p)=Wi*Xi(p), x=x1=x2=х3; y=y1=y2=y3. Y(p)=Y1(p)+ Y2(p)+Y3(p)=W1(p)*X(p)+ W2(p)*X(p)+W3(p)*X(p) = [W1(p)+W2(p)+W3(p)]*X(p).
W э(p)=Y(p)/X(p)=W1(p)+W2(p)+W3(p)=Σni=1Wi(p).
П.Ф.
группы параллельно соед. звеньев равна
сумме отдельных параллельных звеньев.
3) Встречно- параллельное соед. (Соед. с
ОС)
э(p)=Y(p)/X(p)=W1(p)+W2(p)+W3(p)=Σni=1Wi(p).
П.Ф.
группы параллельно соед. звеньев равна
сумме отдельных параллельных звеньев.
3) Встречно- параллельное соед. (Соед. с
ОС)
Схема при которой сигнал с выхода звена или всей системы через какое-либо другое звено подается
опять опять на вход назыв. соед. с обратной связью. Если сигнал обрат. связи складыв. со входным, то ОС назыв. положительная, если вычит. то отрицательная. х1=х±уос. y(p)=W1(p)* X1(p), x1=x±yoc, Yoc(p)=Woc(p)*Y(p). Y(p)= W1(p)* X1(p)= W1(p)* X(p)± W1(p)* Yoc(p)= W1(p)* X(p)± W1(p)* Woc(p)* Y(p). [1±W1(p)*Woc(p)]Y(p)= W1(p)* X(p). Wэ(p)=Y(p)/X(p)= W1(p)/1±W1(p) * Woc(p). Частный случай: 1-я обратная связь.
Wз(p)= Wр(p)/1+Wр(p),
Woc(p)=1.
Wр(p)/1+Wр(p),
Woc(p)=1.
