
- •Содержание Введение………………………………….…………………………..………….……2
- •Введение
- •Задание
- •1. Анализ исходных данных
- •2. Анализ процесса резания как оу
- •3. Разработка структурной схемы сар
- •4. Анализ устойчивости нескорректированной сар
- •5. Выбор корректирующего устройства
- •6. Анализ качества сар
- •Заключение
- •Список использованной литературы
3. Разработка структурной схемы сар
Найдем передаточные функции для элементов схемы.
Преобразователь
энергии (ПЭ).
С точки зрения динамики процесса ПЭ
представляет собой апериодическое
звено второго порядка с постоянными
времени
![]() и
и![]() .
Его передаточная функция имеет вид:
.
Его передаточная функция имеет вид:
![]() ,
,
где
![]() ;
;
![]()
Передаточное
устройство (ПУ).
ПУ является линейным звеном. С точки
зрения динамики является апериодическим
звеном первого порядка с постоянной
времени
![]() ,
тогда:
,
тогда:
![]() ,
,
где
![]() и
и![]() ;
;
![]()
Датчик
обратной связи (ДУ).
Является
апериодическим звеном первого порядка
с постоянной времени
![]() ,
тогда:
,
тогда:
![]() ,
,
где
![]() и
и![]()
![]()
![]()
Двигатель (Д).
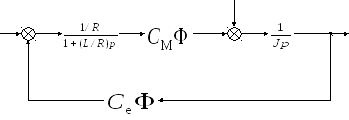
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Электрический двигатель состоит из двух частей: электрической и механической.
![]() А
А
![]() кг*м2
кг*м2
![]() рад/с
рад/с
![]() В*с/рад
В*с/рад
![]() Н*м/А
Н*м/А
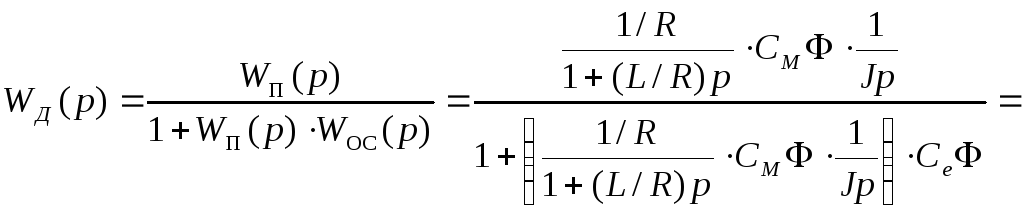
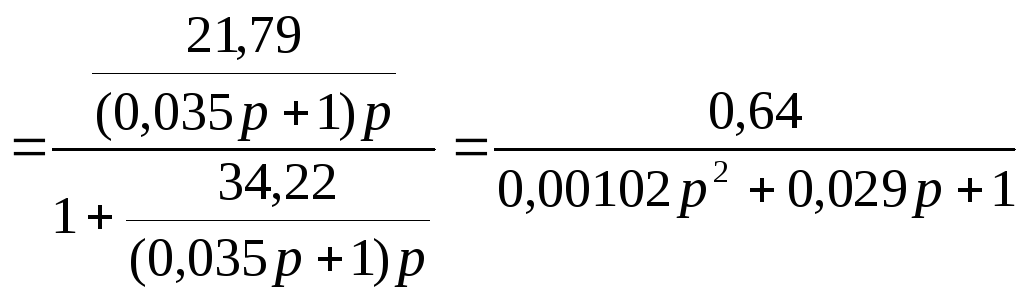
Процесс
резания (ПР).
Описывается уравнением
![]() ,
,![]() .
.
![]() мм
мм
![]() ,
,![]() (2)
(2)
Линеаризуем
эту зависимость. Составим уравнение
касательной к уравнению (2) в точке
![]() м/мин,
которое имеет вид:
м/мин,
которое имеет вид:
![]() ,
,
где
![]()
![]()
![]()
![]() ,
,![]()
Линеаризовав,
получили уравнение касательной
![]() ,
,![]() ,
где
,
где![]() – тангенс угла наклона касательной в
рабочей точке,
– тангенс угла наклона касательной в
рабочей точке,![]() – отклонение касательной от начала
координат.
– отклонение касательной от начала
координат.
,С
S,мм/об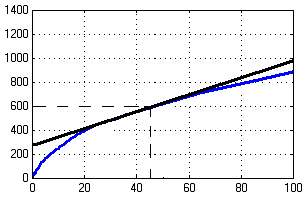
Рис. 3: Кривая процесса резания
![]()
Таким образом, процесс резания предстанет в следующем виде:
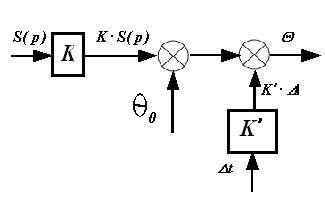
Усилитель (УС). Является безынерционным звеном, его передаточную функцию находим из условия:
![]() ,
,
где
![]() находим из условия:
находим из условия:
![]() ,
,
где
![]() и
и![]()
![]()
![]()
![]()
![]()
4. Анализ устойчивости нескорректированной сар
Построим ЛАХ и ЛФХ разомкнутой системы. Передаточная функция разомкнутой системы будет иметь вид:
![]()
![]() ,
,
Отсюда логарифмические частотные характеристики будут следующими:
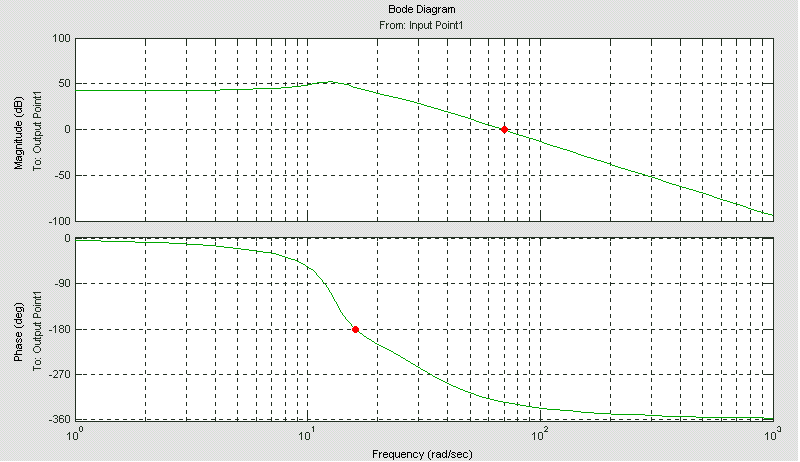
Рис. 4: ЛЧХ разомкнутой системы.
При
анализе построенных ЛАХ и ЛФХ видим,
что нескорректированная система
автоматического регулирования является
неустойчивой, так как ЛФХ пересекает
![]() раньше, чем ЛАХ пересекает 0 (логарифмический
критерий устойчивости). Поэтому необходима
коррекция САР путем введения корректирующего
устройства.
раньше, чем ЛАХ пересекает 0 (логарифмический
критерий устойчивости). Поэтому необходима
коррекция САР путем введения корректирующего
устройства.
5. Выбор корректирующего устройства
Нам необходимо корректирующее устройство с запаздыванием по фазе, поэтому в качестве корректирующего устройства принимаем интегро-дифференцирующее звено с передаточной функцией вида:
![]()
Принимаем
![]()
Значения Т1 и Т2 берем из исходных данных, а значения коэффициентов Т3 и Т4 определяем по частотам среза при построении ЛЧХ корректирующего устройства.
Тогда ЛЧХ скорректированной системы будет иметь вид:
L,дб ,град Lg() Lg()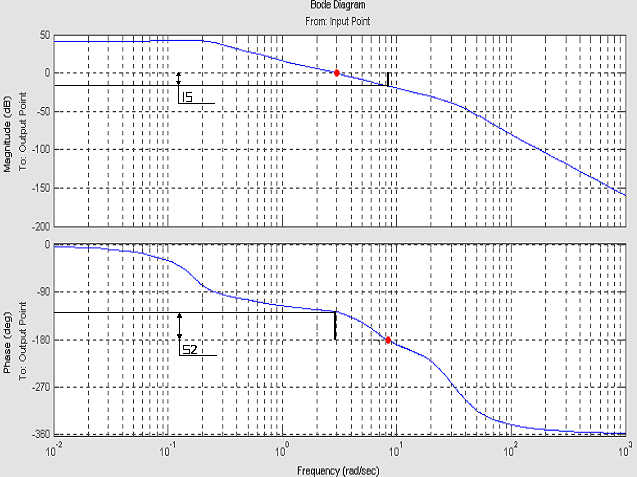
Рис. 4: ЛЧХ скорректированной системы.
Из
графиков видно, что скорректированная
САР является устойчивой. Система имеет
запасы устойчивости по фазе
![]() ,
по модулю
,
по модулю![]() дб,
что удовлетворяет заданным параметрам
качества.
дб,
что удовлетворяет заданным параметрам
качества.
Произведем реализацию корректирующего устройства. Примером интегро-дифференцирующего звена может служить схема на рис. 5.
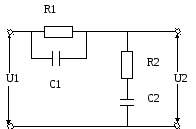
Рис. 5: Корректирующее устройство
В
которой
![]() и
и![]()
Выберем
значения
![]() мкФ,
а
мкФ,
а![]() мкФ,
тогда
мкФ,
тогда
![]() кОм
кОм
![]() кОм
кОм
