
Оглавление
Законы Кеплера 2
Кеплеровы элементы орбиты 4
Типы орбит, о которых говорил Аверьянов: 5
Геоцентрическая абсолютная 6
Типы спутников. 8
Системы навигации и ориентации КА. 9
Законы Кеплера
Зако́ны
Ке́плера —
три эмпирических соотношения, интуитивно
подобранных Иоганном Кеплером на основе
анализа астрономических наблюдений
Тихо Браге. Описывают идеализированную
гелиоцентрическую орбиту планеты. В
рамках классической механики выводятся
из решения задачи двух тел предельным
переходом
![]() /
/![]() → 0, где
,
—
массы планеты и Солнца.
→ 0, где
,
—
массы планеты и Солнца.
 Первый
закон Кеплера (закон эллипсов)
Первый
закон Кеплера (закон эллипсов)
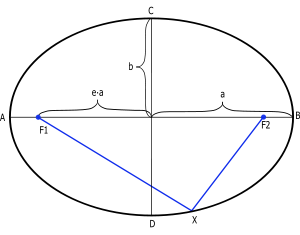
Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце.
Форма
эллипса и степень его сходства с
окружностью характеризуется отношением
![]() ,
где
,
где
![]() —
расстояние от центра эллипса до его
фокуса (половина межфокусного расстояния),
—
расстояние от центра эллипса до его
фокуса (половина межфокусного расстояния),
![]() —
большая полуось. Величина
—
большая полуось. Величина
![]() называется
эксцентриситетом эллипса. При
называется
эксцентриситетом эллипса. При
![]() ,
и, следовательно,
,
и, следовательно,
![]() эллипс
превращается в окружность.
эллипс
превращается в окружность.
Второй закон Кеплера (закон площадей)
 Каждая
планета движется в плоскости, проходящей
через центр Солнца, причём за равные
промежутки времени радиус-вектор,
соединяющий Солнце и планету, описывает
равные площади.
Каждая
планета движется в плоскости, проходящей
через центр Солнца, причём за равные
промежутки времени радиус-вектор,
соединяющий Солнце и планету, описывает
равные площади.
Применительное к нашей Солнечной системе, с этим законом связаны два понятия: перигелий — ближайшая к Солнцу точка орбиты, и афелий — наиболее удалённая точка орбиты. Таким образом, из второго закона Кеплера следует, что планета движется вокруг Солнца неравномерно, имея в перигелии большую линейную скорость, чем в афелии.
Каждый год в начале января Земля, проходя через перигелий, движется быстрее, поэтому видимое перемещение Солнца по эклиптике к востоку также происходит быстрее, чем в среднем за год. В начале июля Земля, проходя афелий, движется медленнее, поэтому и перемещение Солнца по эклиптике замедляется. Закон площадей указывает, что сила, управляющая орбитальным движением планет, направлена к Солнцу.
Кеплеровы элементы орбиты

Кеплеровские элементы орбиты, включая аргумент перицентра (рис.1)
Части эллипса (рис.2)
Кеплеровы элементы — шесть элементов орбиты, определяющих положение небесного тела в пространстве в задаче двух тел:
большая полуось ( ),
эксцентриситет (
 ),
),наклонение (
 ),
),аргумент перицентра (
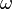 ),
),долгота восходящего узла (
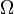 ),
),средняя аномалия (
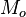 ).
).
Первые два определяют форму орбиты, третий, четвёртый и пятый — ориентацию плоскости орбиты по отношению к базовой системе координат, шестой — положение тела на орбите.
Аргуме́нт перице́нтра — определяется как угол между направлениями из притягивающего центра на восходящий узел орбиты и на перицентр (ближайшую к притягивающему центру точку орбиты спутника), или угол между линией узлов и линией апсид. Отсчитывается из притягивающего центра в направлении движения спутника, обычно выбирается в пределах 0°-360°. Для определения восходящего и нисходящего узла выбирают некоторую (так называемую базовую) плоскость, содержащую притягивающий центр. В качестве базовой обычно используют плоскость эклиптики (движение планет, комет, астероидов вокруг Солнца), плоскость экватора планеты (движение спутников вокруг планеты) и т. д.
Экли́птика (от лат. (linea) ecliptica, от др.-греч. ἔκλειψις — затмение), большой круг небесной сферы, по которому происходит видимое годичное движение Солнца. Современное, более точное определение эклиптики — сечение небесной сферы плоскостью орбиты барицентра системы Земля—Луна. Проще говоря, эклиптика — плоскость вращения Земли вокруг Солнца.
