Answer: b.

70. What statement is wrong?

A. The reference marks are only benchmarks assigned at the beginning of the analysis.

B. Current is a through variable, but voltage is an across variable.

C. One-port network has got two terminals.

D. Linear element of the circuit is such one whose characteristic is a straight line.

E. Battery is considered as voltage source.

Solution:

D – wrong. Linear means that the defining characteristic is a straight line through the origin. Elements whose characteristics do not pass through the origin (even if it’s a straight line) or are not a straight line are said to be nonlinear.

Answer: D.

71. We know R_A, R_B, and R_C for delta. What is R₂ for delta-to-star transformation? (see Fig. 1).

A. R₂ = (R_A + R_B + R_C )/ R_A B. R₂ = R_BR_C/ (R_A + R_B + R_C )

C. R₂ = R_AR_C/ (R_A + R_B + R_C ) D. R₂ = R_BR_A/ (R_A + R_B + R_C )

E. R₂ = R_BR_C/ (R_A + R_B )

Fig.1

Solution:

Answer: C.

7 2 What is the value of current I? (see Fig.2)

A. 2A B. – 1A C. 5A D. 1A E. – 2A

Solution:

Both current sources are directed in the same direction, so the resulting current source will be presented as the sum I=2+3=5A.

Answer: C.

Fig. 2

73. What is equivalent resistance for the circuit below if R₁=15 Ω, R₂=R₅=10 Ω, R₃=R₄=30 Ω?

A. 20 Ω B. 30 Ω C. 40 Ω D. 50 Ω E. 60 Ω

Solution:

Let’s simplify R₃ and R₄ parallel arrangement:

Note: When two resistors connected in parallel and

have the same value R, simplifying to one resistor

will give value R/2.

Now series arrangement of R₁, R₂, R_EQ and R₅ will give

Answer: D.

74. What is the value of V_X for the circuit in Fig.5? A. 10V B.5V C.-5V D.-10V E. –15V

Solution:

Let’s consider the node at the center of the circuit.

Current from left branch is I₁=8/2*10³= 4mA.

By KCL: 4+5–10–i_x=0. i_x= –1mA.

V_x=10*10³*(–1*10^-3)= –10V

Answer: D.

Fig.5

75. What is the value of i_x for the circuit in Fig.5? A. 1mA B.-1mA C.5mA D.-2mA E.2mA

Solution:

Let’s consider the node at the center of the circuit.

Current from left branch is I₁=8/2*10³= 4mA.

By KCL: 4+5–10–i_x=0. i_x= –1mA.

Answer: B.

76. What i-v characteristic corresponds to resistor? Picture_____

A.A B.B C.C D.D E.E

A B C D E

Solution:

We can see i-v characteristic of resistor from Ohm’s Law: V=IR.

Answer: C.

77. What statement is correct?

A. A diode can be used as a voltage divider.

B. Linear element of the circuit is such one whose characteristic is a straight line.

C. Interface between a source and a load is one-port network device.

D. Bilateral element of the circuit is such one whose i-v characteristic curve has odd symmetry about the origin.

E. Bilateral element of the circuit is such one whose i-v characteristic curve has even symmetry about the origin.

Solution:

A – wrong. Only resistor and potentiometer can be used as voltage dividers.

B – wrong. Linear means that the defining characteristic is a straight line through the origin. Elements whose characteristics do not pass through the origin (even if it’s a straight line) or are not a straight line are said to be nonlinear.

C – wrong.

D – correct.

E – wrong. Bilateral means that the i-v characteristic curve has odd symmetry about the origin.

Answer: D.

78. What statement is wrong?

A. Current is a measure of the flow of electrical charge.

B. Voltage is a measure of energy required to move a small charge from one point to another.

C. Power is a measure of the rate at which energy is being transferred.

D. Passive sign convention foresees the current reference arrow is directed toward the terminal with the positive voltage reference mark.

E. When current and voltage have the same algebraic signs the device is delivering power.

Solution:

E – wrong. Under passive sign convention, the current reference arrow is directed toward the terminal with the positive voltage reference mark. Under this convention, the device power is positive when it absorbs power and is negative when it delivers power.

When current and voltage have the same algebraic signs, p will be positive, so the device will absorb power.

Answer: E.

7 9. What is the voltage across points A and B (Fig.6)?

A. 5V B. – 5V C. 29V D. 1V E. – 1V

Solution:

V_AB=2+15–12=5V

Answer: A.

Fig.6

80. What is the correct equation according to KCL for node B for the circuit below?

A. i₃+i₂+i_S2=0 B. i₃-i₂+i_S2=0 C. i₃-i₂-i_S2=0 D. - i₃+i₂+i_S2=0 E.- i₃+i₂-i_S2=0

Solution:

KCL states that the algebraic sum of the currents entering a node is zero at every instant. According to KCL equation for node B is following:

– i₃ + i₂ – i_S2 = 0

Answer: E.

81. When ideal switch is closed, the voltage is equal to______ and current is___, but when it is open current is equal to _____ and voltage is _________.

A. any value, 0, any value,0 B. any value, 0, 0, any value

C. any value, any value, 0, 0 D. 0, any value, 0, any value

E. 0, any value, any value, 0

Solution:

When switch is closed, it’s a short circuit: v=0 when R=0 and i=any value.

When switch is opened it’s an open circuit: i=0 when R=∞ and v=any value.

Answer: D.

82. What element(s) can be used as voltage divider?

A. resistor B. diode C. Transistor D. potentiometer E. resistor, potentiometer

Answer: E.

83. When star-connected circuit is balanced and transformed into the delta, the value of side of equivalent delta is equal to ___ of the star’s ray.

A.3 B.1/3 C.2/3 D.1/2 E. 2

Solution:

Let all resistors in star-connected circuit have the value R, then the value of side of equivalent delta is

, which is equal to 3 times of the star’s ray.

Answer: A.

84. What formula expresses correctly the voltage division rule application for k-th resistor if k of them are connected in series?

A. v_k=v_total*(R_eq/R_k) B.v_k=v_total*(R_k/R_eq) C. v_k=v_total*(R₁/R_eq) D. v_k=v_total/(R_k/R_eq)

E. v_k=v_total*(R_k-1/R_eq)

Solution:

The Voltage Division Rule for k-th resistor if k of them are connected in series is

Answer: B.

8 5. What is the equivalent resistance for the circuit below if all resistances are equal to R?

(between points A and D)

A.0.5R B.R C.1.5R D.2R E.3R

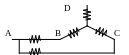
Solution: 1^st way

T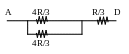 he values of star sides will be three times less, that is R/3, so after reducing resistors in series there will be parallel combination of two resistors with values 4R/3 (R+R/3) in series with one R/3 resistor.

This gives 2R/3+R/3=R.

Answer: B.

2^d way

Points B and C are symmetrical respectively to points A and D, so potential of point B equals to potential of point C. Then we can ignore resistor between points B and C. As a result, we have got the circuit, where four resistors of R are connected in two groups of R/2 (two resistors of R in parallel). So resultant value of Req=R/2+R/2=R

86. What formula expresses correctly the current division rule application for k-th resistor if k of them are connected in parallel?

A. i_k=i_total*(R_eq/R_k) B.i_k=i_total*(R_k/R_eq) C. i_k=i_total*(R₁/R_eq) D. i_k=i_total*(G_k/G_eq)

E. i_k=i_total*(G_eq/G_k)

Solution:

The current division rule for k-th resistor if k of them are connected in parallel is

Answer: D.

87. When delta-connected circuit is balanced and transformed into the star, the value of ray of equivalent star is equal to ___ of the delta’s side.

A.3 B.1/3 C.2/3 D.1/2 E. 2

Solution:

Let all resistors in delta-connected circuit have the value R, then the value of ray of equivalent star is

, which is equal to 1/3 of the delta’s side.

Answer: B.

88. What is correct equation for node B (Fig.7), if we apply node voltage analysis? (G=1/R)

A.– 2Gv_A- 0.5Gv_B+3.5Gv_C=0 B. 2Gv_A- 0.5Gv_B+3.5Gv_C=0

C. 0.5Gv_A+3Gv_B-0.5Gv_C =0 D. – 0.5Gv_A+3Gv_B-0.5Gv_C=0

E . 2.5Gv_A-0.5Gv_B -2Gv_C=i_S Fig. 7

Solution:

V_B(0.5G+2G+0.5G) –V_A(0.5G) –V_C(0.5G)=0

–0.5GV_A+3GV_B–0.5GV_C=0

Answer: D.

89. What statement is wrong?

A. Maximum current available at the interface is the source short-circuit current.

B. When R_L=R_T exists, the source and load are said to be matched.

C. Voltage division and current division are examples of proportionality.

D. Thevenin resistance is equal to input resistance of the circuit.

E. Thevenin and Norton equivalent sources are practical sources.

Solution:

D – wrong. , because Thevenin resistance is equal to lookback resistance of the circuit.

Answer: D.

90. _________ can be defined if we consider the circuit respectively to the interface when all sources are turned off.

A. Thevenin resistance B. input resistance C. lookback resistance

D. Norton resistance E. answers A, C, D are correct

Solution:

Thevenin, Norton and lookback resistance can be defined if we consider the circuit respectively to the interface when all sources are turned off.

Answer: E.

91. v₁(t)= 10cos(1000t - 45°) and v₂(t)= 5cos(1000t+30°). Find the sum of two voltages as phasor.

A. V=11.4+j4.57 B. V=11.4 - j4.57 C. V=4.57+j11.4 D. V=4.57-j11.4

E. V=6+j6.4

Solution:

10cos(1000t - 45°)=10∟- 45° = 10cos(- 45)+j10sin(-45) = 7.07 – j7.07

5cos(1000t+30°)=5∟30° = 5cos(30)+j5sin(30) = 4.33+j2.5

V=(7.07 – j7.07) + (4.33+j2.5) = 11.4 – j4.57

Answer: B.

92. What is time constant for the circuit in Fig.10?

A. 3L/5R B. L/3R C. 2L/3R D. 3R/2L E. 2L/5R Fig. 10

Solution:

T_C=G_NL

;

Answer: A.

93. What is time constant for the circuit whose solution is i_L(t)=30e^-200t-20 mA t≥0.

A. 10 ms B. 20 ms C.1ms D. 5 ms E. 30 ms

Solution:

i_L(t)=[i_L(0) – i_L(∞)]e^-t/Tc+ i_L(∞);

-t/T_C= -200t

1/T_C=200

T_C=1/200=0.005=5 ms

Answer: D.

94. What is differential equation whose solution is v_C(t)= - 20e^-1000t+20 V t≥0.

A. (dv_C/dt)+100v_C= -10u(t) B. (dv_C/dt)+1000v_C= -10u(t)

C. (dv_C/dt)+100v_C= 10u(t) D. (dv_C/dt)+1000v_C= 10u(t)

E. (dv_C/dt)+1000v_C= 20000u(t)

Solution:

v_C(t)= - 20e^-1000t+20 V

RC-circuit with step-response.

General equation is

with general solution of the form

v_C(t)=[v_C(0) – v_C(∞)]e^-t/Tc + v_C(∞)

v_A=v_C(∞)=20V

T_C=R_TC=1/1000; Thus we have

Multiplying by 1000 gives

Answer: E.

95. When we transform the circuit from time domain into S-domain the capacitor must be represented as

A. capacitor admittance and current source, which is connected with the capacitor in parallel

B. capacitor impedance and current source, which is connected with the capacitor in series

C. capacitor impedance and voltage source, which is connected with the capacitor in series

D. capacitor impedance and voltage source, which is connected with the capacitor in parallel

E. A and C are both correct

Solution:

1) Capacitor impedance and voltage source, which is connected with the capacitor in series;

2) Capacitor admittance and current source, which is connected with the capacitor in parallel.

Answer: E.

96. What is correct inverse Laplace transform V_C(t) for the function V_C(s)=(- 0.6s/s²+4)

A. – 0.6 cos2t B.0.6cos2t C.- 0.6sin2t D.0.6sin2t E.0.6e^2t

Solution:

Answer: A.

97. When we transform the circuit from time domain into S-domain the admittance of inductor is

A.Y_L(s)=Ls B. Y_L(s)=Ls with i_L(0)=0 C. Y_L(s)=1/Ls D. Y_L(s)=1/Ls with i_L(0)=0

E. Y_L(s)=1/L

Solution:

Z_L=Ls with i_L(0)=0; Y_L=1/Z_L=1/Ls with i_L(0)=0;

Answer: D.

97. Define impedance of the circuit in the s-domain respectively points A and B (fig.11).

A.Z(s)=RCs+1 B.Z(s)=Cs+2R C.Z(s)=RCs+R D.Z(s)= R(RCs+1)/(RCs+2)

E. Z(s)=R(RCs+2)/(RCs+1) Fig.11

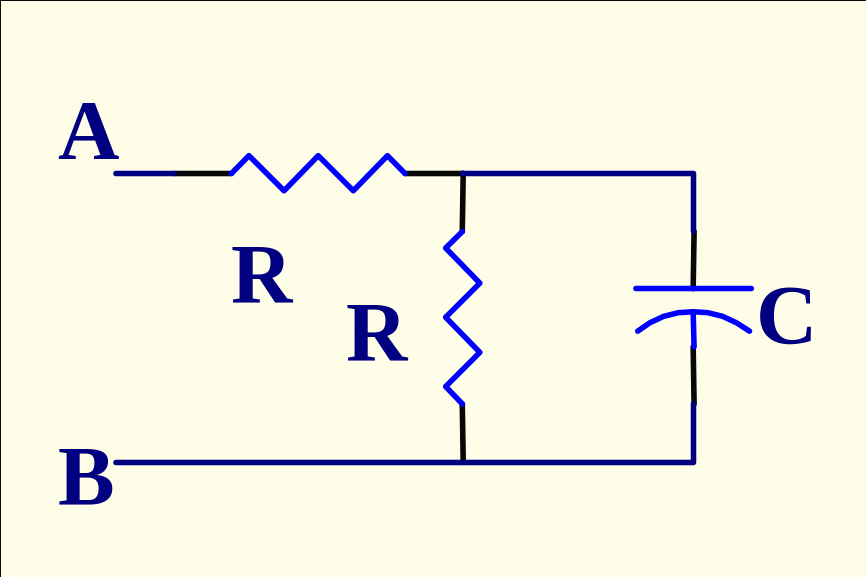
Solution:

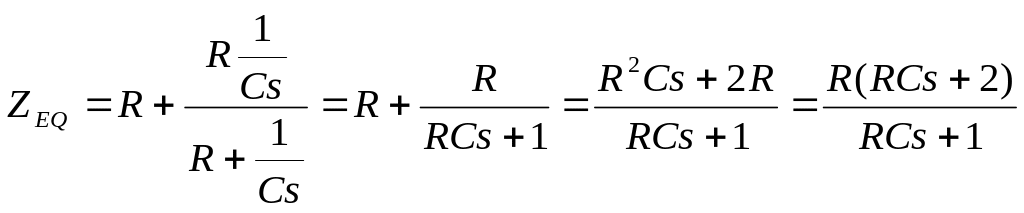
Answer: E.

98. Find the mistake in process of transformation of time-domain circuit in s-domain circuit.

A. wrong representation of the capacitor impedance

B. wrong representation of the inductor impedance

C. wrong representation of the capacitor initial condition current source

D. wrong representation of the inductor initial condition current source

E . there is no mistake in process of circuit’s conversion

Solution:

I(t)=I(s);

Z_R(s)=R;

Z_C(s)=1/Cs;

I_C(s)=CsV_C(s) – CV_C(0);

Z_L(s)=Ls;

I_L(s)=(1/Ls)*V_L(s)+i_L(0)/s;

Wrong representation of the inductor initial condition current source.

Answer: D.

99. The time domain equation is 10i₁+0.02(di₁/dt)-0.02(di₂/dt)=100. What is the view of the equation in the s-domain?

A. (10+0.02s)I₂(s)-0.02sI₁(s)=100/s B. (10+0.02s)I₁(s)-0.02sI₂(s)=100

C. (10+0.02s)I₁(s)-0.02sI₂(s)=100/s D. (10+0.04s)I₁(s)-0.04sI₂(s)=100/s

E. 0.02sI₁(s)-0.02sI₂(s)=100/s

Solution:

time domain	s-domain
f(t)	F(s)
df(t)/dt	sF(s)-f(0-)
100	100/s

t-domain:

10i₁+0.02(di₁/dt)-0.02(di₂/dt)=100

s-domain:

10I₁+0.02sI₁ – 0.02sI₂=100/s

(10+0.02s)I₁ – 0.02sI₂=100/s

Answer: C.

100. What must be Z_load to have maximum average power transfer conditions fulfillment, if Z_T=50+j70?

A. 50 - j70 B. 50+j70 C. 70+j50 D. 70 – j50 E. 100+j20

Solution:

if X_T = – X_L, then denominator is minimized, I is maximized and P is maximized, thus Z_load to have maximum average power transfer conditions fulfillment, if Z_T=50+j70 has to be 50-j70.

Answer: A.

101. What numbers of natural poles are corresponded to sinusoidal type of response?

A)2 and 4

B) 1 and 3

C) 1 and 9

D) 1 and 5 E) only 6

Answer: D

102. Define impedance of the circuit in the s-domain respectively points A and B (fig.12).

A ).Z(s)=RLCs²+Ls+R/RCs+1

B).Z(s)=CLs+2R

C).Z(s)=RLCs+R

D).Z(s)= R(RLCs+1)/(RCs+2)

E) Z(s)=R(RLCs+2)/(RCs+1)

Fig.12

Solution:

Z_R(s)=R

Z_C(s)=1/Cs

Z_L(s)=Ls

Z_eq(s)=(R/Cs)/(R+1/Cs)+Ls=( RLCs²+Ls+R)/( RCs+1)

Answer:A

103. Find the mistake in process of transformation of time-domain circuit in s-domain circuit.

A) wrong direction of the capacitor initial condition current source

B) wrong representation of the inductor impedance

C) wrong representation of the capacitor initial condition current source

D) wrong representation of the inductor initial condition current source

E) there is no mistake in process of circuit’s conversion

Answer: A

104.Network function is dependence between

A)parameters of the circuit

B) parameters of the circuit in the s-domain

C) parameters of the circuit in the time-domain

D) parameters of the circuit in the phasor-domain

E) input and output in the s-domain

Answer: E

105. The Laplace transform of the waveform f(t)=3[cos2t]u(t)+3[sin2t]u(t) is

A).(-3s+4)/s(s+2

B). .(-3s+4)/s²(s+2)

C) .(-3s)/s(s+2)

D) 4/s(s+2)

E)(3s+6)/(s²+4)

Solution:

Ј{f(t)}= Ј{3[cos2t]u(t)}+ Ј{3[sin2t]u(t)}=3s/( s²+4) + 6/ s²+4 = (3s+6)/(s²+4)

Answer: E

106. When we transform the circuit from time domain into S-domain the admittance of capacitor is

A).Y_C(s)=Cs

B) Y_C(s)=Cs with v_C(0)=0

C) Y_C(s)=1/Cs

D) Y_C(s)=1/Cs with v_C(0)=0

E) Y_C(s)=C/s

Solution:

Y_C(s)=1/Z_C(s)

Z_C(s)=1/Cs with v_C(0)=0

Y_C(s)=Cs with v_C(0)=0

Answer: B

107. The time domain equation is 10i+0.2(di/dt)=50e^-100t. What is the view of the equation in the s-domain?

A)0.2sI(s)=50/(s+100)

B) 10I(s)=50/(s+100)

C) (10s²+0.2s)I(s)=50/(s+100)

D) (10+0.2s)I(s)=50/(s+100)

E). (10+0.2s)I(s)=50

Solution:

10Ј{i}+0.2Ј{di/dt}=Ј{50e^-100t }

Ј{di/dt}=sI(s)-I(0)= sI(s)

Ј{i}=I(s)

10 I(s)+0.2sI(s)= 50/(s+100)

(10+0.2s)I(s)=50/(s+100)

Answer: D

108. Impedance of the circuit in s-domain is defined as Zeq(s)=R(RCs+2)/(RCs+1).

Select the value of R and C such that Zeq(s) has a zero at s= -5000rad/s. R=____, C=___.

A)10kΩ, 40nF

B) 5kΩ, 20nF

C) 15kΩ, 20nF

D) 7kΩ, 20nF E) 20kΩ, 30nF

Solution:

Zeq(s)=R(RCs+2)/(RCs+1) s=-5000 Zeq(s)=0

R(RCs+2)=0

RCs+2=0

5000RC=2

RC=1/2500=4*10^-4

R=10*10³ Ω=10kΩ

C=40 nF

Answer: A

109. For the circuit in fig.13 the switch was in position 2 for a long time, now it switches to position 1. What is correct differential equation for the case in s-domain?

A )25sI(s)=50/(s+100)

B) 25I(s)+0.01sI(s)-0.04=50/s

C) (25s²+0.01s)I(s)=50/(s+100)

D) (25+0.01s)I(s)=50/s

E) (25+0.01s)I(s)=50

Fig.13

Solution:

V_R(s)=RI_L(s)

V_L(s)=LsI_L(s)-LI_L(0)

V(s)=50/s

I_L(0)=100/25=4 A

V_R(s)+V_L(s)=V(s)

RI_L(s)+LsI_L(s)-LI_L(0)=50/s

25I_L(s)+0.01sI_L(s)-0.01*4=50/s

Answer: B

110. Impedance of the circuit in s-domain is defined as Zeq(s)=R(RCs+2)/(RCs+1).

Select the value of R and C such that Zeq(s) has a zero at s= -2000rad/s. R=____, C=___.

A)1kΩ, 1μF

B) 5kΩ, 1 μF

C) 10kΩ, 1μF

D) 1kΩ, 10μF

E) 10kΩ, 10μF

Solution:

Zeq(s)=R(RCs+2)/(RCs+1) s=-2000 Zeq(s)=0

R(RCs+2)=0

RCs+2=0

2000RC=2

RC=10^-3

R=10^-3 Ω=1k Z1=R²+(1/C)²

C=10^-6 F=1μF

Answer: A

111. If a waveform has odd symmetry the Fourier series consist of _______components.

A) cosine

B) sine

C) cosine and sine

D) cosine and dc

E) sine and dc

Solution:

sine, because a waveform is said to have odd symmetry if -f(-t)=f(t)

sin(-x)=-sin(x)

Answer: B

112. For the circuit in fig. 14 what is the voltage across capacitor when the switch was in position 1 for a long time and closes to position 3 now?

Fig.14

A) 20e^-t/RC –5

B) 15e^-t/RC –5

C) 10e^-t/RC –5

D) 20e^-t/RC +5

E) 20e^-t/RC +10

Solution:

V(0)=15 V

V_A =-5 V

V(t)=( V(0)- V_A ) e^-t/RC + V_A =20e^-t/RC –5 ,V

Answer: A

113. For the circuit in fig.14 what type of function is applied to RC circuit?

A)pulse

B) step C)sinusoidal D) square wave E)exponent

Answer: B

114. For the circuit in fig.14 in what passage the amplitude of capacitor voltage is reached maximum during the transient?

A) 1-3

B) 2-3

C) 3-2

D) 1-2 E) 3-1

Solution:

V(0)=15 V

V_A =-10 V

V(t)=( V(0)- V_A ) e^-t/RC + V_A =25e^-t/RC –10 ,V

For other passages the amplitude is lower than 25V

Answer: D

115. For series RL circuit voltage of the source is equal to 10cos10t, V. Current through the circuit is 2cos(10t -30˚), A. Define the value of inductance.

A) 1H

B) 0.75H

C) 0.5H

D) 0.25H

E) 0.1H

Solution:

Z_R=R

Z_L=jwL

Z_eq=R+jwL

Z_eq=V/I=10cos10t/2cos(10t -30˚)=(10∟0˚)/(2∟-30˚)=5∟30˚=4.33+j2.5

Z_L=jwL=j2.5

wL=2.5 w=10rad/s

L=0.25 H

Answer: D

116. What is angular frequency for the signals v(t)=10cos10t, V?

A) 10Hz

B) 1.59Hz

C) 10rad/s

D)

1.59rad/s

E) 3.18Hz

Solution:

10rad/s, because v(t)= V_A cos(t+φ) - angular frequency, then w=10rad/s

Answer: C

117. For RC circuit when frequency increases 2 times the impedance of the circuit _______.

A)increases 2 times

B) decreases 2 times

C) increases more than 2 times

D) decreases more than 2 times

E) decreases less than 2 times

Solution: Z₁=R²+(1/C)², Z₂=R²+(1/2C)², so if R=2Ω, 1/C=2Ω, 1/2C=1Ω, Z₁=2²+2²=8 Ω

Z₂=2²+1²=5 Ω. Z₁/Z₂=8/5=1.26

Answer: E

1 18. Express the signal, whose line spectra are represented in the picture on the right.

A) 8cos(2πf₀t+60˚)+5cos(2π3f₀t-30˚)+ 3cos(2π4f₀t+45˚)

B) 8cos(2πf₀t+60˚)+5cos(2π3f₀t-30˚)

C) 5cos(2πf₀t+60˚)+3cos(2π3f₀t-30˚)+ 10cos(2π4f₀t+45˚)

D) 8cos(2πf₀t+60˚)+5cos(2π3f₀t+30˚)+ 3cos(2π4f₀t+45˚)

E) 8cos(2πf₀t+60˚)+5cos(2π2f₀t-30˚)+ 3cos(2π3f₀t+45˚)

Answer: A

119. Find the average power in R=10 Ω if current i(t)=10sin 10t+5sin30t+2sin50t flows through it.

A)320W

B)525W

C)435W

D)480W

E)645W

Solution:

P_av=RIrms²

Irms² =(I₁²+I₂²+I₃²+…+In²)/2= (10²/2+5²/2+2²/2)=64.5

P_av=RIrms² =645,W

Answer: E

120. Total harmonic distortion is defined according to the formula:

A)(√Y₁²+Y₂²+Y₃²+…+Yn²)/│Y1│

B) │Y1│/(√Y₁²+Y₂²+Y₃²+…+Yn²)

C) (√Y₂²+Y₃²+…+Yn²)/│Y1│

D) │Y1│/(√Y₂²+Y₃²+…+Yn²)

E) │Y1│*(√Y₂²+Y₃²+…+Yn²)

Answer: C

121. Define Thevenin impedance for the circuit in fig.15. Z_T(s)=____ Fig.15

A) R/(RCs+1) B) RC/(RCs+1) C) R/(Rs+1)

D) Rs/(RCs+1) E) Rs/(RC+1)

Solution:

Z_R(s)=R

Z_C(s)=1/Cs

Z_T=(R/Cs)/ (1/Cs+R)=R/(RCs+1)

Answer: A

122. Define the current of short circuit I_SC(s) for the circuit in fig.16.

fig.16

A)I_SC(s) = V_S/s

B) I_SC(s) = RV_S/s

C) I_SC(s) = V_S/Rs

D) I_SC(s) = V_S/RCs

E) I_SC(s) = V_S/RCs+1

Solution:

Ј{V(t)}= V_S/s

I_SC(s) = V_S/Rs

Answer: C

123. Which of the elements are non-linear?

A) resistor

B) inductor

C) diode

D) capacitor

E) potentiometer

Answer: C

124. In series RLC circuit oscillations takes place during the transient when we have got_____ response.

A)overdamped

B) critically damped

C) underdamped D) overdamped or underdamped

E) there are no oscillations at all

Answer: C

125. The unit of inductance is

A).C

B)F

C).H

D)V*s/A

E) answers C and D are both correct

Answer: E

126. Total harmonic distortion for the pure sinusoid is equal to