§4. Введение в анализ

1. Определение предела функции.

Пусть функция f(x) определена на некотором проме­жутке Х и пусть точка x₀  Х или x₀  Х. Число А называется пределом функции f(x) в точке x = x₀, если для любого числа ε > 0 существует число δ > 0 такое, что для всех x  Х, удовлетворяющих неравенству 0<x - x₀ < δ, выполня­ется неравенство

 f(x) — А < ε .

2. Определение непрерывности функции.

Функция f(x) называется непрерывной в точке x₀, если она определена в некоторой окрестности точки x₀ и в самой точке x₀ и если .

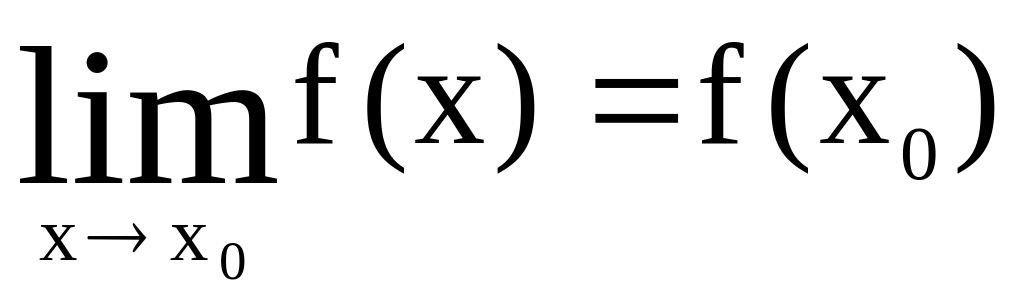3. Раскрытие неопределенностей вида и .

Пример1. Найти .

Решение. Имеем неопределенность вида . Для раскрытия этой неопределенности разложим числитель и знаменатель на множители, а затем сократим на общий множитель (x +2). Получаем:

(так как неопределенность устранена, то теперь подставляем x = -2)

Пример 2. Найти:

.

Решение. Имеем неопределённость вида . Разделим на x² числитель и знаменатель дроби:

,

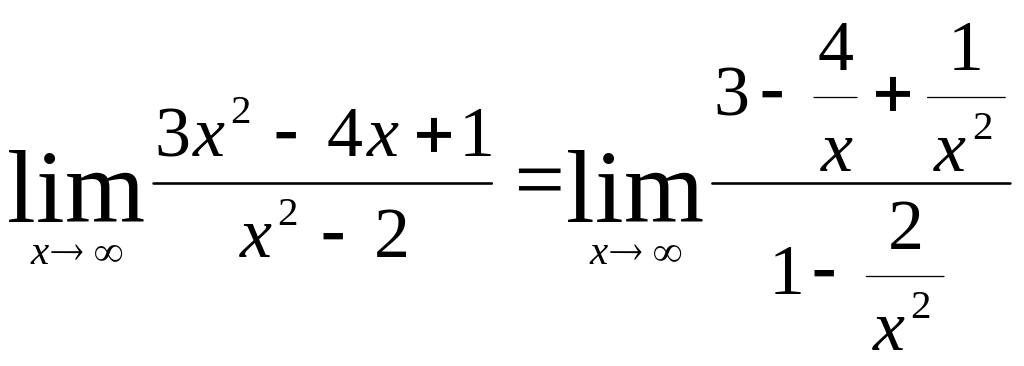так как и , то получаем =

4. I замечательный предел.

.

Так как sin 0 = 0, то это неопределенность вида .

Пример 3. Найти .

Решение. Имеем неопределенность вида . Для раскрытия данной неопределенности перепишем tg2x через sin2х и cos2х и применим I замечательный предел.

так как cos 0=1, имеем

где y=2x, если , то .

5. II замечательный предел.

или .

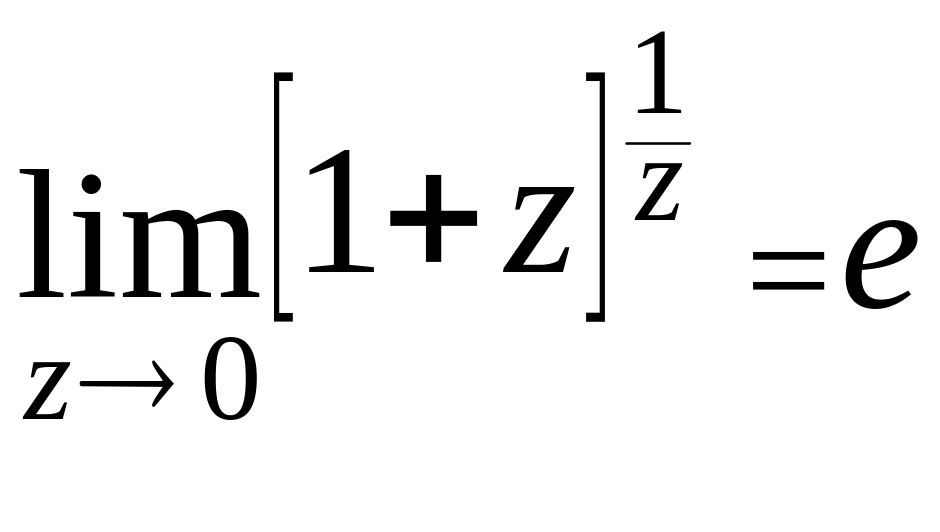Неопределенность вида [1^∞].

Пример 4. Найти .

Решение. Имеем неопределенность вида [I^∞], поэтому используем II замечательный предел.

Делаем подстановку: => x = 3t. Если x —>∞ , то t —> ∞.

,

так как .

6. Раскрытие неопределённости вида [∞ — ∞].

Пример 5. Найти

.

Решение. Имеем неопределённость вида [∞-∞], для устранения которой домножим и разделим на сопряжённое выражение, то есть на

.

7. Непрерывность функции в точке.

Пример 6. Функция у задана различными аналитическими выражениями для различных областей изменения аргумента x:

x + 2, если x ≤ -2;

у = x² - 4, если -2 < x < 1;

4 – 2x, если x ≥ 1.

Требуется:1) найти точки разрыва функции, если они существуют;

2) найти односторонние пределы и скачок функции в точке разрыва;

3) сделать чертёж.

Решение. Данная функция определена и непрерывна в интервалах (-∞; -2), (-2;1) и (1;+∞). При x = -2 и x = 1 меняется аналитическое выражение функции, и только в этих точках функция может иметь разрыв.

Определим односторонние пределы в точке x =-2:

y(-2)=-2+2=0.

Следовательно, в точке x = -2 функция непрерывна. Определим односторонние пределы в точке x = 1:

Отсюда следует, что в точке x = 1 функция разрывна. Пределы слева и справа конечны, значит , разрыв первого рода.

Скачком функции в точке разрыва называется абсолютная величина разности между ее правым и левым предельными значениями. Следовательно, в точке x = 1 скачок функции ∆ = |2 - (-3)| = 5.

Построим график функции

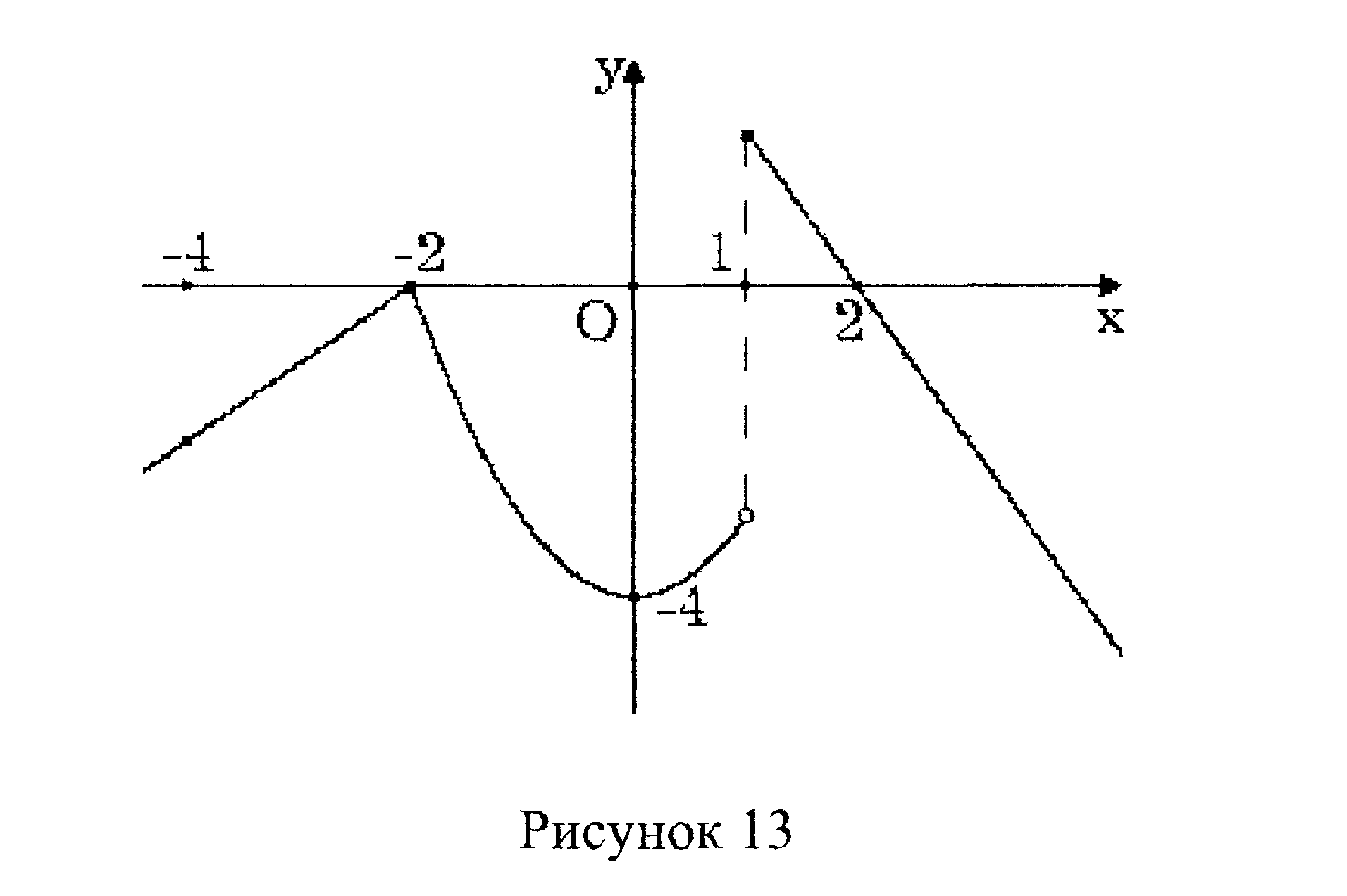
5. Дифференцирование

1. Производной функции у = f(x) в точке x₀ называется предел при ∆х —> 0 отношения приращения функции в этой точке к приращению аргумента (при условии, что этот предел существует).

Нахождение производной называется дифференцированием функции.

2. Правила дифференцирования:

1) (u±)′= u'±';

2) (u  )′ = и' v + и v';

3) .

4) Если функция и = (x) дифференцируема в точке x⁰, а функция y = f(u) дифференцируема в точке U⁰ =(x), то сложная функция у = f[(x)] дифференцируема в точке x₀ и y'(x₀₎=y'(U₀)u'(x₀),

3. Таблица производных основных элементарных функции.

1) C' = 0 2) (xⁿ)' = nx^n-1

3) (a^x)׳ = a^x · ln a 4) (e^x)'=e^x

5) (sinx)' = cosx 6) (cosx)' = -sinx

7) (tg x)' = 8) (ctg x)' =

9) (arcsin x)' = 10) (arccos x)' = -

II) (arctg x)' = 12) (arcctg.x)' =

13) (log_a x)' = 14) (ln x)' = 1/x

Пример 1. Найти производную функций:

1 ) f(x} = 5 + х³ + sin x + 3 In x,

2) f(x)= ,

3) f{x) =x  arctg x - ln(l+x²).

Решение:

1) f'(x) = (5 + x³ + sin x + 3 In x)' = (5)' + (x³ )' + (sin х)' + 3(ln x)' =

= 0 + Зх² + cos x + 3  = Зх² + + cos x.

2) f'(x) =

.

3) f'(x)= (х · arctg x)' - · (1п(1 + x²))' =

=x'arctg x + x(arctg x)' - .

4. Производная функции, заданной неявно.

Пример 2. Найти , если задана функция

cos x - tg(2y) + у²  x = 0.

Решение. Вычисляем производную по x, считая у функцией от x:

(cos х - tg(2y) + у² х)' =0

- sin x - 2y' + 2у · у' х + у² =0.

Выражаем y': 2y 

y'=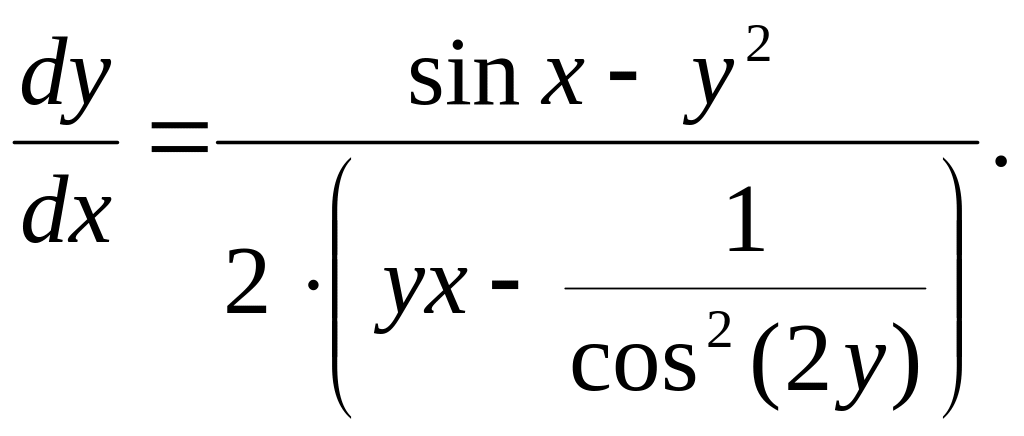

5. Производные высших порядков.

Производная f'(x) называется производной первого порядка. Производная от f'(x) называется производной второго порядка (или второй производной) от функции f(x) и обозначается у" или f''(\x). Произ­водная от f''(\x) называется производной третьего порядка и т.д.

Пример 3. Найти у''(х), если у = ln (2х -3).

Решение: 1) у' = ,

2) y" (x)= =2 ((2x – З)^-1)' = -2  (2х - З)^-2 · 2 =- .

6. Дифференцирование функций, заданных параметрически. Производные первого и второго порядка функции у = f(x), заданной параметрически функциями x = (t), y= (t), выражаются формулами:

Пример 4. Найти и , если .

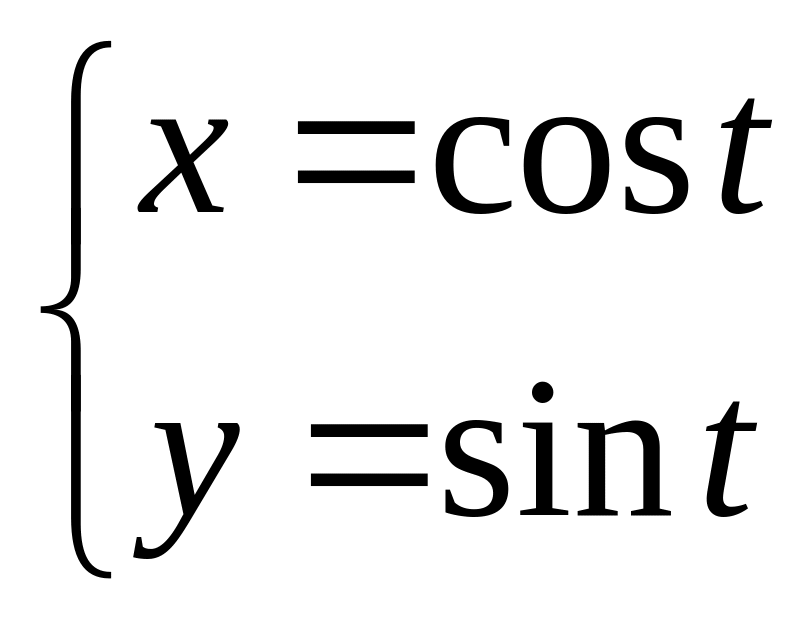Решение. Считаем

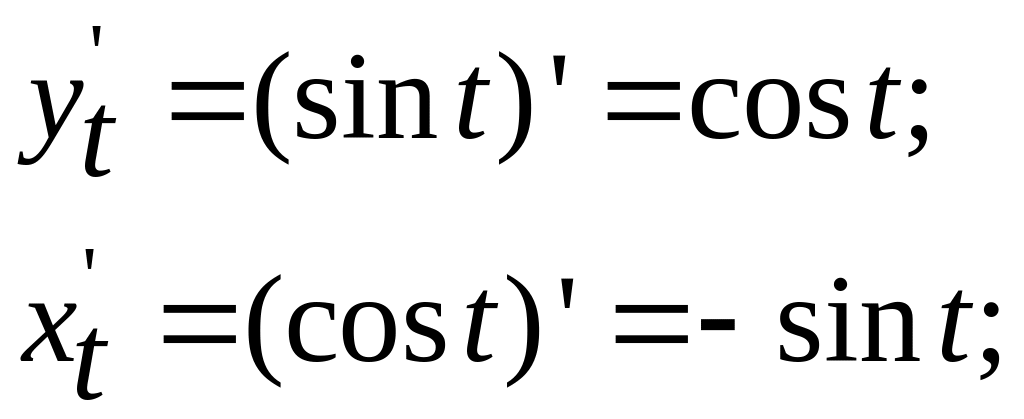
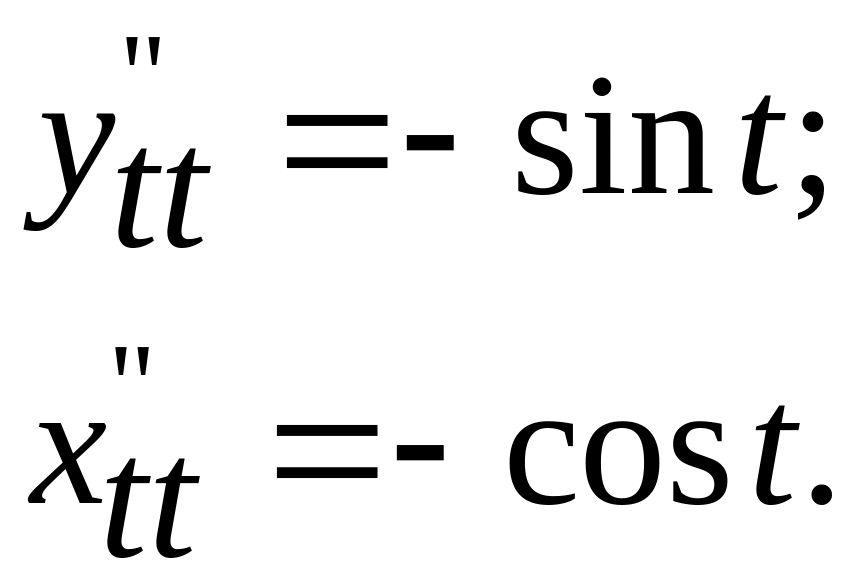
Следовательно,

.

7. Правило Лопиталя.

Если , то когда последний предел существует.

Если , то , когда последний предел существует.

Пример 5. Найти

Решение. Имеем неопределённость вида ; применяя правило Лопиталя, получим:

Неопределённости вида [0∞] и [∞-∞] сводятся путём алгебраических преобразований к неопределенностям вида и , а затем раскрываются с помощью правила Лопиталя.

8. Исследование функции и построение графика.

Пример 6. Исследовать функцию у = и построить её график.

Решение. 1) Ищем область определения данной функции:

x  (-∞; 2) U(2; +∞ ); x = 2 – точка разрыва.

2) Функция не является ни чётной, ни нечетной, так как

у(-x)  у(x) и у(-x)  -у(x).

3) Ищем асимптоты графика функции:

а) вертикальной асимптотой является прямая х = 2;

l.

б) наклонные асимптоты:

k₁= ;

b₁=

= .

Следовательно, прямая у = x + 3 является наклонной асимптотой при x∞.

Аналогично вычисляем k₂ = и b₂ = получаем также у = x + 3.

в) Горизонтальные асимптоты – это частный случай наклонных асим­птот при условии, что k = 0.

Иначе можно найти горизонтальную асимптоту по формуле:

b =

Следовательно, горизонтальной асимптоты не существует.

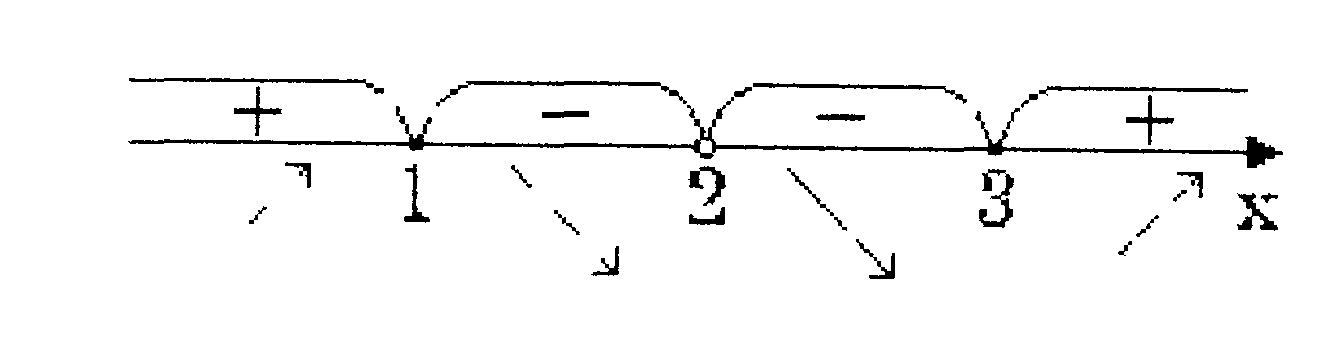
4) Ищем критические точки первого порядка (то есть те точки, где первая производная равна нулю или не существует).

Первая производная равна нулю при x=1 и x=3 и не существует при x = 2.

5) Ищем интервалы возрастания и убывания функции, точки макси­мума и минимума.

у'0) > 0 => на (-∞; 1) функция возрастает.

y'(1.5) < 0 ==> на (1; 2) функция убывает.

y'(2.5) < 0 ==> на (2; 3) функция убывает.

y'(4) > 0 => на (3; + ∞) функция возрастает.

Следовательно, x = 1 – точка максимума, x = 3 – точка минимума.

у(1) = 3; y(3) = 7. Обозначим точкой А(1; 3), точкой В(3; 7).

6) Найдем критические точки второго порядка (точки, в которых вторая производная равна нулю или не существует).

y"=

=

Вторая производная ни при каком значении аргумента не равна нулю; не существует при x = 2.

7) Определим интервалы выпуклости и вогнутости графика функции;

точки перегиба.

y"(1) < 0 ===> на (-∞; 2) функция выпуклая;

y"(3) > 0 ===> на (2; + ∞) график функции вогнутый.

Точек перегиба нет.

8) Строим график функции.

9. Наибольшее и наименьшее значения функции.

Пример 7. Разложить число 10 на два положительных слагаемых так, чтобы произведение их было наибольшим.

Решение. Пусть x – первое число, тогда (10 — x) – второе слагаемое.

Обозначим f(x) = x . (10 - x) = 10х - х² – произведение этих чисел.

Считаем f'(x} = 10 - 2х.

Находим критические точки этой функции:

10-2x=0=>x=5

f'(x) > 0 ==> на (0; 5) функция возрастает;

/'(6) < 0 ==> на (5; 10) функция убывает; следовательно,

x = 5 - точка максимума. f_наиб=f(5)= 25.

Ответ: 10 = 5 +5.

10. Уравнения касательной и нормали.

10.1. Уравнение касательной к графику функции f(x) в точке x₀.

y = f'(x₀)(x-x₀) + f(x₀),

где x₀ – заданное значение, f(x) – заданная кривая.

10.2. Уравнение нормали к графику функции f(x) в точке x₀ .

y=

Пример 8. Составить уравнения касательной и нормали к кривой в точке, соответствующей значению параметра t = t₀.

x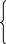 =t³ - 4t + 1

y=t² – 4t + 3 , t₀=1.

Решение. Так как кривая задана параметрическими уравнениями, то найдём:

x₀ = x(t₀) = 1- 4 + 1 = -2; f(x₀) = y₀ = y(t₀) = 1 + 3 – 4 = 0;

f'(x) = 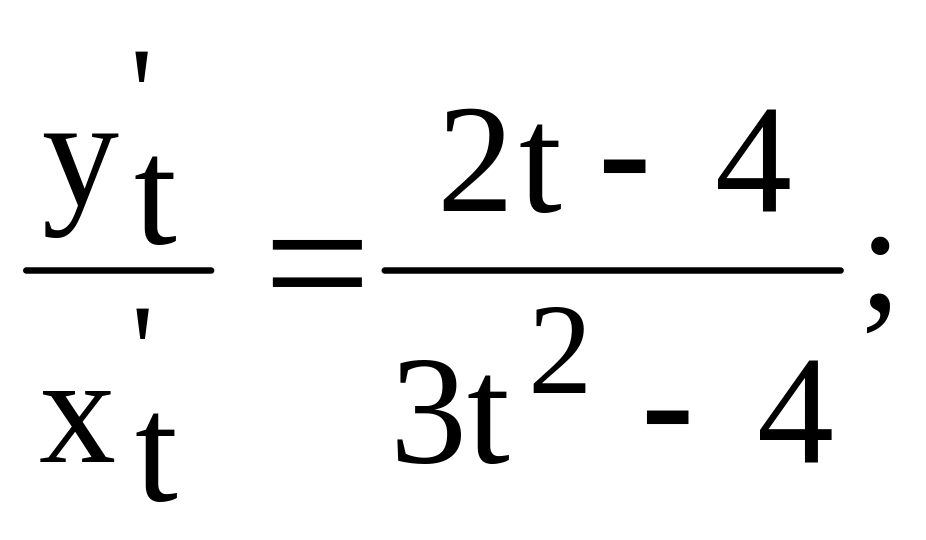f'(x₀) =

Уравнение касательной: y = 2(x+2) +0 = 2x + 4.

Уравнение нормали: y =