10.4. Источники стабильного тока

Неизменное значение постоянного тока, независимое от пара­метров цепи (нагрузки), может обеспечить только идеальный гене­ратор тока с бесконечно большим динамическим сопротивлением, ВАХ которого параллельна оси напряжения (рис. 10.14). ВАХ ре­ального генератора тока приближается к ВАХ идеального генера­тора только в некотором интервале значений напряжения. При этом его динамическое сопротивление хотя и очень большое, но не бесконечно большое.

Заметим, что выходная характеристика биполярного транзи­стора в схеме с ОБ близка к ВАХ идеального генератора тока. Сле­довательно, транзистор, включен­ный по схеме с общей базой, прак­тически может выполнять функ­цию генератора тока. Однако на практике используется не один, а два и более транзисторов, кото­рые обеспечивают не только получение большого динамического сопротивления, но и слабую зави­симость самого тока генератора от нестабильности напряжения источников питания и температурной нестабильности элементов схемы.

Расчет динамического сопротивления сводится к расчету выход­ного сопротивления транзисторного каскада по малосигнальным эк­вивалентным схемам, как это делалось при рассмотрении парамет­ров усилительного каскада в § 10.1.2. Расчет же влияния эксплуатационных факторов на нестабильность тока должен проводиться по уравнениям токов биполярного транзистора в статическом режиме (по статической модели Эберса - Молла).

Наиболее существенной причиной нестабильности тока (смеще­ния рабочей точки) источника стабильного тока (ИСТ) является тем­пературная нестабильность параметров элементов цепи. Темпера­турная нестабильность БТ заключается в основном в изменении обратного тока коллекторного перехода , изменении статического коэффициента передачи тока базыи изменении напряжения на эмиттерном переходе при заданном токе перехода. Для кремниевых транзисторов, используемых в ИС, изменениене имеет сущест­венного значения, поэтому температурная нестабильность каскадов определяется в основном изменениямии. Температурная не­стабильность каскадов на полевых транзисторах обусловлена изме­нением напряжения отсечки (порогового напряжения) и крутизны ха­рактеристики. Температурная нестабильность интегральных рези­сторов зависит от их типа и характеризуется температурным коэф­фициентом сопротивления (ТКС).

В гибридных схемах необходимая стабильность постоянного то­ка достигается методами классической электроники путем выбора цепей подачи напряжения на переходы и применением отрицатель­ной обратной связи. В гибридных ИС имеются значительно большие возможности использования резисторов с большими сопротивлени­ями, чем в полупроводниковых ИС.

На рис. 10.15 приведено несколько простых вариантов схем ис­точников стабильного тока, предназначенных для полупроводнико­вых ИС [30]. На основе этих схем разработаны сложные схемы ИСТ.

Самая простая схема ИСТ показана на рис. 10.15,а. Это схема транзисторного каскада, у которого базовый ток задается с помощью делителя и , а в эмиттерной цепи имеется резистор , ослабля­ющий влияние температуры на коллекторный ток (см. § 10.1.2). Со­противления и выбираются так, чтобы ток значительно пре­вышал базовый ток. В этом случае изменение режима работы тран­зистора, приводящее к изменению тока, не будет заметно влиять на величину напряженияЕ_о на резисторе , определяющего напряже­ние транзистора, да и сам расчет становится проще. При указан­ном выборе и <<и

(10.41)

С другой стороны, . Поэтому стабилизируемый ток с учетом (10.41)

(10.42)

Если бы можно было пренебречь величиной , то

(10.43)

При а = 1 , т.е. ток повторяет («отражает») значение , которое называют иногда опорным током. В общем случае. Такая связь токовиобъясняет существующее название схемы «токовое зер­кало» или «отражатель тока».

Из выражения (10.42) следует, что при неизменных сопротивле­ниях ток ИСТ будет зависеть только от и, влияющего на . Ес­ли напряжение источникастабилизировано, то останется только влияние нестабильности. Температурная чувствительность на­пряжения кремниевого БТ (при изменении на 1°С) составляет

(10.44)

Поэтому при изменении температуры значение тока не будет оста­ваться постоянным. Нестабильность тока, связанная с нестабильно­стью и определяемая вторым слагаемым в (10.42),

(10.45)

Чем больше сопротивление резистора в эмиттерной цепи, тем меньше абсолютная нестабильность. При= 1 кОм= 2,5 мВ/°С и при = 1°С= 2,5 мкА.

Динамическое сопротивление в простейшей схеме, рассчитанное по малосигнальной эквивалентной схеме при дифференциальных параметрах = 30 Ом,= 3·10^-4, = –0,99,= 3·10 ^-7 См, сопротивлении = 1 кОм и дополнительном сопротивлении в цепи базы = 1 кОм оказывается близким к 1 МОм.

На рис. 10.15 показаны еще три модифицированные схемы ИСТ, имеющие лучшую температурную стабильность, чем схема на рис. 10.15,а [30]. Эти варианты отличаются тем, что в цепь тока включен компенсационный р-n-переход – интегральный бипо­лярный транзистор в диодном включении, называемый опорным.

В схеме на рис. 10.15,б имеется опорный транзистор , но в от­личие от схемы на рис. 10.15,а отсутствуют резисторы и. Если оба транзистора идентичны по размерам и параметрам, то прибудут равны токии(). Так каки, то

(10.46)

Температурная нестабильность тока по-прежнему будет опре­деляться температурной нестабильностью напряжения(оди­наковой для обоих транзисторов). Однако она зависит и от сопро­тивления. При увеличениипо сравнению св формуле (10.42) нестабильность уменьшится.

Дальнейшее повышение стабильности тока достигается в схеме на рис. 10.15,б переходом к транзисторам, отличающимся площа­дью эмиттерных переходов ():

(10.47)

На практике это отношение достигает пяти. Так как по-прежнему , то

(10.48)

Теперь вместо (10.46) получим

(10.49)

что приводит к снижению нестабильности, характеризуемой вто­рым слагаемым, в b раз по сравнению со схемой с идентичными транзисторами. Недостатком схемы является то, что фиксация токов определяется отношением площадей эмиттеров, а его не­возможно сделать более пяти. Когда отношение опорного и ос­новноготоков более пяти, рекомендуется использовать схему, изображенную на рис. 10.15,в. В ней снова используются иденти­чные по размерам транзисторы(b=1), но в отличие от простей­шей схемы (рис. 10.15,а) отсутствует резистор . Уравнение Кирхгофа для нижнего контура схемы

(10.50)

Основной ток , так как. В качестве опорного диода (как и ранее) используется транзистор в диодном включении. Как и прежде, можно считать, т.е. Выражение (10.50) мож­но теперь записать в виде , откуда следует

(10.51)

В отличие от выражения (10.42) температурная нестабильность определяется температурной нестабильностью разности и. Эта разность может стать равной нулю, если через идентич­ные эмиттерные переходы проходят одинаковые токи (), что возможно только при=. Но это означает, что вместо выраже­ния (10.51) можно написать очевидное соотношение

(10.52)

Однако следует заметить, что температурная нестабильность все-таки останется, так как опорный ток зависит от в соот­ветствии с формулой

(10.53)

но эту нестабильность можно ослабить, если . Тогда

В ряде ИС требуются ИСТ с очень малым значением тока при большом значении опорного тока (). В этих случаях используют модифицированную схему, показанную на рис. 10.15,г. Для этой схемы

(10.54)

Используя ВАХ идеализированного перехода (3.40), можно написать

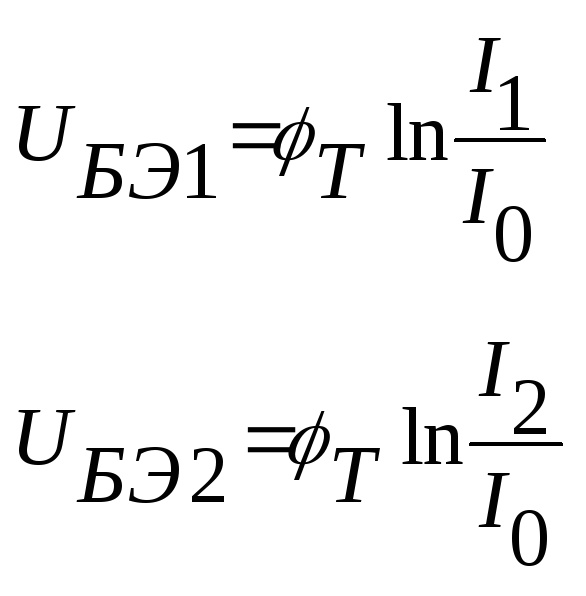(10.55)

где– тепловой ток идентичных переходов. Из выражений (10.54) и (10.55) получим

(10.56)

По заданному току можно определить из (10.56) необходимое со­противление эмиттерного резистора:

Следует заметить, что при малых токах (десятки микроампер) для одинаковых эмиттеров обоих транзисторов требуемое сопротивление достигает 1 МОм, что трудновыполнимо. Поэтому и в этой схеме ис­пользуются транзисторы с неодинаковыми площадями эмиттеров (= 1 ...5), что позволяет понизить сопротивление резистора.

Наконец, отметим, что существуют более сложные схемы, чем приведенные на рис. 10.15, с лучшими характеристиками.