18.3. Частотные характеристики сигналов и систем.

Частотный отклик системы. Допустим, что двумерная ЛИС-система имеет импульсный отклик h(kx,ly). Подадим на вход системы сигнал вида комплексной синусоиды:

s(n,m) = exp(jnx_x+jmy_y),

где _x и _y – значения частоты сигнала соответственно по координатам x и y. Принимая x = 1, y = 1 и выполняя двумерную свертку (18.2.5), получаем:

z(n,m) =h(k,l) exp[j_x(n-k)+j_y(m-l)] =

= exp(jn_x+j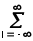m_y) h(k,l) exp(-jk_x-jl_y) = H(_x,_y) exp(jn_x+jm_y).

H(_x,_y) = h(k,l) exp(-jk_x-jl_y). (18.3.1)

Таким образом, выходной сигнал представляет собой комплексную синусоиду с теми же значениями частоты, что и у входного сигнала, с изменением амплитуды и фазы за счет комплексного множителя H(_x,_y), который носит название частотного отклика (частотной характеристики) системы. Для дискретных сигналов частотный отклик периодичен с периодом 2 по обеим частотным переменным:

H(_x+2k,_y+2l) = H(_x,_y).

Пример расчета частотного отклика системы.

Определить частотную характеристику системы с импульсным откликом:

h(0,0) = 0.25, h(0,1) = 0.125, h(1,0) = 0.125, h(1,1) = 0.0625.

Частотный отклик:

H(_x,_y) =h(n,m)exp(-jn_x-jm_y) = 0.25+0.125[exp(-j_x)+exp(j_x)+exp(-_y)+exp(j_y)]+

+0.0625[exp(-j_x-j_y)+exp(-j_x+j_y)+exp(j_x-j_y)+exp(j_x+j_y)] = 0.25(1+cos _x)(1+cos _y).

Система является примером двумерного фильтра нижних частот. Частотный отклик системы на плоскости (_x,_y), приведенный на рис. 18.3.1, имеет осевую симметрию с коэффициентом передачи 1 в центре (_x=0, _y=0) со спадом до нуля при _x= и _y=.

Рис. 18.3.1. Частотная характеристика ФНЧ.

При разделимости импульсного отклика частотный отклик многомерных систем также является разделимой функцией:

h(k,l)= q(k)g(l) Q(_x)G(_y)= H(_x,_y)

Q(_x) = _k q(k) exp(-jk_x). G(_y) = _l g(l) exp(-jl_y).

Импульсный отклик системы. Выражение (18.3.1), по существу, описывает разложение функции Н(_x,_y) в двумерный рад Фурье с коэффициентами разложения в виде отсчетов импульсного отклика h(k,l), т.е. прямое преобразование Фурье. Очевидно, что обратным преобразованием Фурье с интегрированием в пределах одного периода из частотного отклика H(_x,_y) можно получить импульсный отклик системы:

h(k,l) = H(_x,_y) exp(jk_x+jl_y) d_xd_y. (18.3.2)

Пример расчета импульсного отклика фильтра.

Определить импульсный отклик идеального фильтра низких частот с прямоугольной частотной характеристикой вида: H(_x,_y) = 1 при |_x|a<, |_y|b<; H(_x,_y) = 0 в остальных случаях.

Импульсный отклик: h(k,l) = exp(jk_x+jl_y) d_x d_y.

Система разделима: h(k,l)= exp(jk_x) d_x exp(jl_y) d_y= .

Пример расчета неразделимого импульсного отклика.

Определить импульсный отклик идеального кругового фильтра нижних частот:

H(_x,_y) = 1 при _x²+_y² <R²<²; H(_x,_y) = 0 в остальных случаях.

Вычисления по круговой области целесообразно выполнять в полярных координатах: =,

arctg(_y/_x), = arctg(m/n), при этом выражение 18.3.2 перепишется в следующем виде:

h(n,m) = exp[j cos(-)] dd=

= J_o() d= J₁(R) /,

где J_o(…), J₁(…)- функции Бесселя 1-го рода 0-го и 1-го порядков соответственно.

На рис. 18.3.2 приведена пространственная форма импульсного отклика фильтра, расчет которой проведен при R = 1 с ограничением по N = 10 и M = 10, и сечения отклика по координате m.

Рис. 18.3.2. Круговой низкочастотный фильтр (справа - сечения по координате m).

Свойства двумерного преобразования Фурье. Вышеприведенные преобразования импульсного отклика в частотный отклик и наоборот представляют собой двумерные дискретные преобразования Фурье с прямоугольным растром дискретизации информации, эквивалентные одномерным преобразованиям. На двумерные преобразования с прямоугольным растром переносятся и другие свойства одномерных систем. В частности:

1. Фурье-преобразования сигналов.

S(_x,_y) = _n _m s(n,m) exp(-jn_x-jm_y). (18.3.3)

s(n,m) =S(_x,_y) exp(jn_x+jm_y) d_xd_y. (18.3.4)

2. Теорема о свертке.

z(n,m) = h(n,m) _** s(n,m)  H(_x,_y) S(_x,_y) = Z(_x,_y).

z(n,m) = c(n,m) s(n,m)  C(_x,_y) _** S(_x,_y) = Z(_x,_y).

3. Основные свойства Фурье-преобразования.

1) Линейность (в том числе для любых комплексных чисел a и b):

аs(n,m)+bz(n,m)  aS(_x,_y)+bZ(_x,_y).

2) Пространственный сдвиг:

s(n-N,m-M)  S(_x,_y) exp(-jN_x-jM_y).

3) Дифференцирование:

dS(_x,_y)/d_x  -jn s(n,m),

dS(_x,_y)/d_y  -jm s(n,m),

d²S(_x,_y)/(d_x d_y)  -nm s(n,m).

4) Комплексное сопряжение:

х*(n,m)  S*(-_x,-_y).

Вещественная и мнимая части Фурье-образов последовательностей s(n,m):

S(_x,_y) = S*(-_x,-_y).

Re [S(_x,_y)] = Re [S(-_x,-_y)].

Im [S(_x,_y)] = -Im [S(-_x,-_y)].

5) Теорема Парсеваля:

_n _m s(n,m) s*(n,m) = S(_x,_y) S*(_x,_y) d_x d_y.

В частности, при s(n,m) = s(n,m):

_n _m |s(n,m)|² = |S(_x,_y)|² d_x d_y,

где левая часть уравнения представляет собой полную энергию дискретного сигнала s(n,m), a функция |S(_n,_m)|² - спектральную плотность энергии сигнала.