18. Вычисление потенциала по напряжености поля. Поле равномерно заряженной бесконечной плоскости.
задается формулой:
,
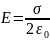где σ — поверхностная плотность заряда.
Разность потенциалов между точками,
которые лежат на расстояниях
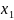и
от плоскости, равна (используем формулу
)
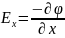19. Вычисление потенциала по напряжености поля. Поле двух бесконечных равномерно заряженных плоскостей.
задается формулой:
,
где σ — поверхностная плотность заряда.
Разность потенциалов между плоскостями,
между которыми расстояние равно d
(используем формулу
),
равна
20. Вычисление потенциала по напряжености поля. Поле равномерно заряженной сферической плоскости.
радиус R с общим зарядом Q вне сферы
(r>R) задается формулой:
E=
(
)
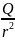разность потенциалов между двумя
точками, лежащими на расстояниях
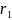и
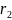от центра сферы (r1>R, r2>R, r2>r1), равна
(1)
Если положить r1=r и r2=, то потенциал поля вне сферической поверхности, согласно формуле (1), равен выражению
Внутри сферической поверхности потенциал везде одинаков и равен
График зависимости φ от r
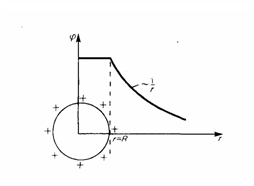
21. Вычисление потенциала по напряжености поля. Поле равномерно заряженного шара.
радиуса R с общим зарядом Q вне шара (r>R) вычисляется, как известно, по формуле E= ( ), поэтому разность потенциалов между двумя точками, лежащими на расстояниях r1 и r2 от центра шара (r1>R, r2>R, r2>r1), задается формулой .
В любой точке, лежащей
внутри шара на расстоянии r' от его центра
(r'<R), напряженность определяется
выражением: E=
(
)
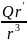Значит, разность потенциалов между
двумя точками, которые расположены на
расстояниях r1' и r2' от центра шара (r1'<R,
r1'<R, r2'>r1' ), равна
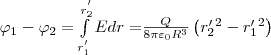
22. Вычисление потенциала по напряжености поля. Поле равномерно заряженной бесконечной нити (цилиндра).
радиуса R, который
заряжен с линейной плотностью τ, вне
цилиндра (r>R) задается формулой: E=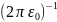
(
)
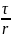Значит, разность потенциалов между
двумя точками, которые расположены на
расстояниях r1 и r2 от оси заряженного
цилиндра (r1>R, r2>R, r2>r1), равна
23. Типы диэлектриков. Поляризация диэлектриков.
Диэлектриками
называются вещества, которые в обычных
условиях практически не проводят
электрический ток, их удельное
сопротивление
в раз больше, чем у металлов. Согласно
представлениям классической физики, в
диэлектриках, в отличие от проводников,
нет свободных носителей заряда, которые
могли бы под действием электрического
поля создавать ток проводимости.
Диэлектрики, как и
любые вещества, состоят из атомов и
молекул. В целом молекулы нейтральны,
тем не менее, они взаимодействуют с
электрическим полем. Например, в случае,
когда симметрия молекулы отлична от
сферической, ее можно представить в
виде электрического диполя. Электрический
дипольный момент молекулы
, где q - суммарный заряд ядер или
электронов; l - вектор, представляющий
собой плечо эквивалентного диполя.
Молекулы, обладающие
электрическим дипольным моментом,
называют полярными. Полярным диэлектриком
является вода; следующие вещества: CO;
N2O; S2O; NH; HCl также имеют в своем составе
полярные молекулы. В объеме вещества
дипольные моменты молекул распределены
по разным направлениям хаотическим
образом, так что их сумма равна нулю
.
Молекулы, у которых
положения эквивалентного положительного
и эквивалентного отрицательного заряда
совпадают и, следовательно, дипольный
момент каждой молекулы равен нулю (
),
называют неполярными. Такие вещества,
как
состоят из неполярных молекул.
Если диэлектрик внести в электрическое поле, то это поле и сам диэлектрик претерпевают существенные изменения.