Задание № 25.
Запишите дифференциальное уравнение малых движений системы с одной степенью свободы с учетом сил линейного сопротивления и его решения в случае большого и предельного сопротивления. Как называются эти решения? Каким свойством обладают силы линейного сопротивления?
Две материальные точки А и В, соединенные тонким стержнем длины l, движутся в вертикальной плоскости таким образом, что скорость середины стержня всегда направлена вдоль стержня от точки А к точке В. Какой тип связи наложен на эту механическую систему? Запишите математическое выражение для этой связи и определите число степеней свободы данной системы.
Систему сил, действующую твердое тело, совершающее плоское движение, привели к центру масс С. Получили равный нулю главный вектор и отличный от нуля главный момент Мс. Вычислить обобщенную силу, соответствующую линейному перемещению центра масс s.
Ползун А массой m1, кг скользит в поле сил тяжести вниз по прямолинейной направляющей, направленной под углом 600 к горизонтальной прямой, а ползун В массой m2, кг скользит по горизонтальной направляющей и имеет в данный момент ускорение ав = 3,6 мс-2, направленное вправо. Ползуны А и В связаны посредством цилиндрических шарниров невесомым стержнем. Используя общее уравнение динамики определить ускорение ползуна А, если стержень образует угол = 600 с прямой по которой скользит ползун А.
Коэффициент инерции механической системы с одной степенью свободы равен 3, а коэффициент жесткости – 12. Запишите дифференциальное уравнение собственных колебаний данной механической системы, вычислите частоту и период собственных колебаний. Определите амплитуду и начальную фазу колебаний, если
.
Нарисуйте график собственных колебаний
системы.
Шар массой m, кг ударяется о гладкую неподвижную плоскость, причем вектор скорости шара после удара образует угол = 600 с нормалью, проведенной вертикально вверх к плоскости в точке удара. Определить угол падения шара, если коэффициент восстановления равен .
Задание № 26.
Запишите дифференциальное уравнение вынужденных колебаний системы с одной степенью свободы без учета сопротивления и его решение при отсутствии резонанса. Перечислите свойства этого решения.
Систему сил, действующую твердое тело, совершающее плоское движение, привели к центру масс С. Получили главный вектор Rc и главный момент Мс. Вычислить обобщенную силу, соответствующую углу поворота тела .
Ползун А массой m1, кг скользит в поле сил тяжести вверх по прямолинейной направляющей, направленной под углом 600 к горизонтальной прямой, а ползун В массой m2, кг скользит по горизонтальной направляющей влево. Ползун А имеет в данный момент ускорение аа = 3,6 мс-2. Ползуны А и В связаны посредством цилиндрических шарниров невесомым стержнем. Используя общее уравнение динамики определить ускорение ползуна В, если стержень образует угол = 600 с прямой по которой скользит ползун А.
Механизм, изображенный на рисунке, находится в равновесии. Для заданного положения механизма, определить отношение возможных перемещений точек А и D.
Коэффициент инерции механической системы с одной степенью свободы равен 6, коэффициент жесткости – 6, а обобщенный коэффициент сопротивления – 12. Запишите дифференциальное уравнение собственных колебаний при наличии линейного сопротивления для данной механической системы. Какому случаю сопротивления соответствует данное уравнение? Вычислите коэффициент затухания и запишите вид решения уравнения для данного случая, если
.
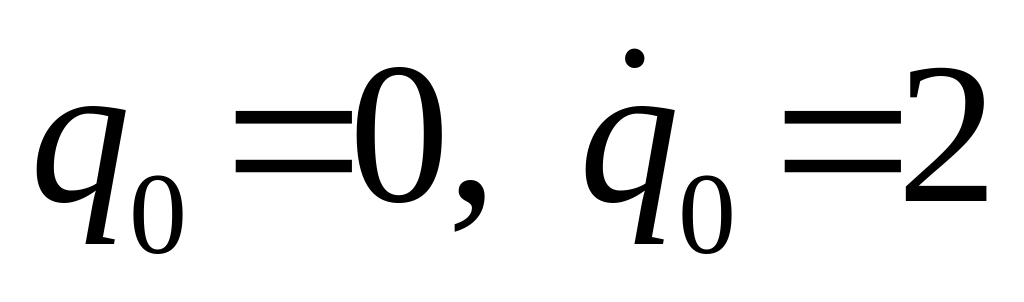Шар массой m, кг ударяется о гладкую неподвижную плоскость, причем вектор скорости центра шара до удара образует угол = 450 с нормалью, проведенной вертикально вверх к плоскости в точке удара. Определить коэффициент восстановления, если угол отражения шара = 600.