Задание № 19.

1. Запишите формулы для кинетической и потенциальной энергии механической системы с одной степенью свободы при малых отклонениях от положения устойчивого равновесия. Почему коэффициент жесткости системы величина положительная?

2. Однородное круглое колесо радиусом R, м и массой m, кг катится без проскальзывания по горизонтальной поверхности под действием пары сил с моментом М. Коэффициент трения качения равен . Выбирая в качестве обобщенной координаты угол поворота колеса, вычислить обобщенную силу.

3. Тело А массой m₁, кг подвешено на нити, перекинутой через неподвижный блок С, массой m₃, кг. К концу нити привязан груз В массой m₃, кг. Тело А опускается вниз. Определить ускорение, с которым движутся грузы.

4. Механизм, изображенный на рисунке, находится в равновесии. Для заданного положения механизма, определить отношение возможных перемещений точек А и В.

5. Дифференциальное уравнение собственных колебаний механической системы с одной степенью свободы имеет вид: 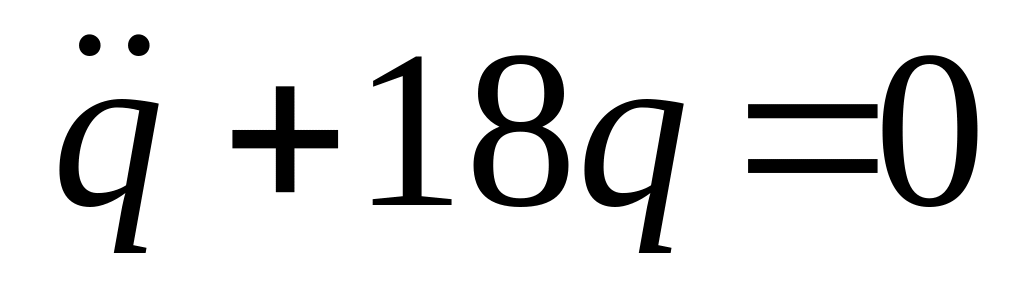. Определите частоту и период собственных колебаний системы. Вычислите амплитуду и начальную фазу колебаний, если . Нарисуйте график собственных колебаний системы.

6. Однородная квадратная пластина АВСD может вращаться вокруг неподвижной вертикальной оси О₁О₂, лежащей в ее плоскости и отстоящей от центра тяжести пластины на расстоянии, равном четверти стороны. Сторона пластины равна a, м. Ось вращения в точке О₁ закреплена с помощью подпятника, а в точке О₂ – подшипника. Определить положение центра удара пластины, если на нее действует ударный импульс.

Задание № 20.

1. Запишите дифференциальное уравнение малых колебаний системы с одной степенью свободы и вид решения. Как называется решение данного уравнения, перечислите его свойства.

2. Материальная точка закреплена в точке В невесомой нити АВ. Точка движется в вертикальной плоскости. Точка А нити закреплена и остается неподвижной. Определите тип связи наложенной на материальную точку и запишите математическое выражение для этой связи.

3. Однородное круглое колесо радиусом R, м и массой m, кг катится без проскальзывания по горизонтальной поверхности под действием пары сил с моментом М. Коэффициент трения качения равен . Выбирая в качестве обобщенной координаты линейное перемещение центра масс колеса, вычислить обобщенную силу.

4. Ползун А массой m₁, кг скользит в поле сил тяжести по вертикальной прямолинейной направляющей и имеет в данный момент ускорение а_а = 0,6 мс^-2, направленное вниз, а ползун В массой m₂, кг скользит по горизонтальной направляющей вправо. Ползуны А и В связаны посредством цилиндрических шарниров невесомым стержнем. Используя общее уравнение динамики определить ускорение ползуна В, если стержень образует угол  = 60⁰ с вертикальной прямой.

5. Коэффициент инерции механической системы с одной степенью свободы равен 2, коэффициент жесткости – 18, а обобщенный коэффициент сопротивления – 20. Запишите дифференциальное уравнение собственных колебаний при наличии линейного сопротивления для данной механической системы. Какому случаю сопротивления соответствует данное уравнение? Вычислите коэффициент затухания и запишите вид решения уравнения для данного случая, если .

6. Шар массой m = 2, кг движется поступательно и упруго ударяется о гладкую неподвижную плоскость, причем вектор скорости центра шара до удара направлен по нормали к плоскости в точке удара. Определить изменение кинетической энергии шара, если коэффициент восстановления равен 0,3, а величина скорости центра шара до удара  v = 4 мс^-1.