4. Кодирование сообщений при передаче по каналу без помех возможность оптимального (эффективного) кодирования

Под кодированием будем понимать отображение состояний некоторой системы (источника сообщений) с по­мощью состояний сложного сигнала, который представляет собой последовательность из п элементарных сигналов. Множество У состояний элементарного сигнала образует алфавит кода размера т_у. При т_у=2 элементарный сигнал имеет два состояния, которые обозначим через 1 и 0. Состояние слож­ного сигнала описывается последовательностью из нулей и единиц, которая называется кодовым словом. Если кодо­вые слова имеют разную длину, то код называется нерав­номерным, а если одинаковую, то код называется равно­мерным .

Пусть источник сообщений вырабатывает последователь­ность из k букв, причем x_i буква в этой последовательности появляется п_i раз. Каждой букве поставим в со­ответствие кодовое слово с длиной, равной l_i (посимвольное кодирование). Тогда длина соответствующей последователь­ности из кодовых слов будет равна

Это равенство можно представить в виде

При неограниченном увеличении числа букв К в последова­тельности относительная частота появления x_i буквы с ве­роятностью, равной единице, совпадает со значением вероят­ности p_i появления этой буквы. Поэтому с вероятностью, равной единице, выполняется равенство

где — по определению средняя длина кодового слова. Длина последовательности кодовых слов L является случайной величиной, но значительные отклонения ее от среднего значения маловероятны при неограниченном возрастании К.

Таким образом, источник сообщений с вероятностью, рав­ной единице, вырабатывает типичные последовательности, длина которых мало отличается от их среднего значения К .

Поскольку время передачи сообщений определяется дли­ной L , то имеется возможность его сокращения за счет уменьшения средней длины кодового слова . Задача оптимального кодирования заключается в определе­нии однозначно декодируемых кодовых слов с такими длина­ми, при которых их средняя длина минимальна.

Префиксные коды

При неравномерном коде в длинной последовательности кодовых слов не всегда удается определить начало и конец переданной буквы.

Однако однозначное декодирование всегда имеет место в случае применения кодов, обладающих свойством префик­са (приставки). Код обладает свойством префикса, если ни одно кодовое слово не является началом (приставкой) какого-либо другого кодового слова.

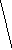
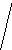
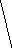
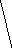
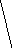
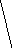
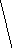
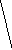
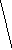
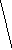
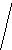
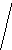
Все множество кодовых слов, максимальная длина кото­рых не превосходит число, равное l, геометрически удобно изобразить в виде узлов дерева (рис. 2). Дерево представ­ляет собой множество точек (узлов), соединенных отрезками, которые называются ребрами дерева. Из каждого узла выхо­дят m_y ребер, каждое из которых изображает соответствую­щий символ алфавита кода. Слова, состоящие всего из одной буквы, изображаются узлами первого порядка. Их число равно m_y. Слова, состоящие из двух букв, изображаются узлами второго порядка и т. д. Причем узлов (слов) К-го порядка в m_y раз больше, чем узлов (К-1)-го порядка, поскольку каждый узел предыдущего порядка порождает m_y узлов следующего порядка. Конкретный вид кодового слова определяется по изображающему его узлу как последова­тельность ребер (букв), которые соединяют основание дерева с указанным узлом. В случае префиксных кодов на пути, соединяющем основание дерева с изображающим узлом, не может быть промежуточных изображающих узлов.

3

2

1

Рис. 2 Полное троичное (m_x=3) кодовое дерево третьего

порядка (l=3): 1, 2, 3 - узлоы первого, второго, третьего порядков

Поскольку с помощью дерева (рис. 2) можно изобразить все кодовые слова с длиной, меньшей или равной l, то оно называется полным деревом порядка l с алфавитом объ­ема т_у.