Производительность дискретного источника сообщений

Кодовое слово, которое вырабатывает источник, будем за­писывать в виде ÿ буква

(символ) алфавита сk порядковым номером в слове. Напри­мер, пусть k=5, a i₅==3. Это значит, что пятой буквой в сло­ве является третья буква алфавита. Обозначим через Х_k мно­жество букв (алфавит), из которых выбирается k-ÿ буква

слова. В нашем случае все множества X_k(k=1,n) состоят из одних и тех же т_x букв. Когда не требуется указывать мес­то буквы в слове, i-þ букву алфавита будем обозначать че­рез x_i.

Количество информации, которое в среднем несет отдель­ное слово, равно энтропии

,

где суммирование ведется по всему множеству слов. Опреде­лим производительность источника Н_И как предел отношения

количества информации, которое в среднем несет отдельно слово, к числу букв в слове п при неограниченном возраста нии п:

(6)

Если буквы в слове статистически независимы (вероят- ность выбора очередной буквы не зависит от состава пред шествующих ей букв), то

где .

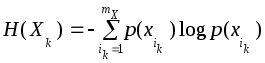Источник со статистически независимыми буквами сооб­щений будет стационарным, если вероятность выбора 1-й бук­вы алфавита не зависит от того, какое место в слове она за­нимает .

В этом случае

H(X₁,...,X_n)=nH(x)

н производительность источника (бит/символ)

.

Часто производительность источника измеряется количе­ством информации , которое он вырабатывает за одну секунду (—количество букв за одну секунду). Максималь­ная производительность источника достигается, когда все бук­вы алфавита появляются с равными вероятностями. В этом случае .

Марковские источники сообщений

Рассмотренная модель дискретного источника сообщений имеет сравнительно узкую область применения, поскольку ре­альные источники вырабатывают слова при наличии статисти­ческой зависимости между буквами. В реальных источниках вероятность выбора какой-либо очередной буквы зависит от всех предшествующих букв. Многие реальные источники дос­таточно хорошо описываются марковскими моделями источ­ника сообщений. Согласно указанной модели условная веро­ятность выбора источником очередной , буквы зависит

только от предшествующих. Математической моделью со­общений, вырабатываемых таким источником, являются цепи Маркова -ãî порядка. В рамках указанной модели условная вероятность выбора i_k -й буквы

.

Если последнее равенство не зависит от времени, то есть справедливо при любом значении k, источник называется од­нородным. Однородный марковский источник называется стационарным, если безусловная вероятность выбора очеред­ной буквы не зависит от k . В дальнейшем бу­дем иметь дело только со стационарными источниками. Вы­числим производительность источника для простой цепи Маркова (=l). В этом случае вероятность

.

Прологарифмировав последнее равенство, получим

.

Это равенство показывает, что индивидуальное количест­во информации, которое несет слово, равно количеству ин­формации, которое неcет первая буква, плюс количество ин­формации, которое несет вторая буква при условии, что пер­вая буква уже принята, и т. д.

Усредняя равенство по всем словам, получим количество информации, которое в среднем несет каждое слово:

.

Поскольку источник стационарный, то энтропия не зависит от k и равна

.

Подставляя полученный результат в (6) и учитывая, что всегда , имеем

.

В случае марковской цепи -ãî порядка H_и вычисляется ана­логично и равна Н_И=Н(Х₊₁|X,..., X₁).

Таким образом, производительность марковского источ­ника равна неопределенности выбора очередной буквы при условии, что известны v предшествующих.

Для производительности марковского источника всегда справедливо неравенство

.

Максимального значения, равного logm_X, производитель­ность источника достигает, когда отсутствует статистическая зависимость между буквами в слове и когда все буквы алфа­вита вырабатываются с равными вероятностями. Очевидно, максимальная производительность источника полностью определяется размером алфавита т_X .

Для того чтобы характеризовать, насколько полно исполь­зует источник возможности алфавита, вводится параметр

называемый и з б ы т о ч н о с т ь ю.

Для передачи заданного количества информации, равного I, требуется п=I/H_И букв, если производительность источника равна H_И. В случае, когда производительность источника дос­тигает своего максимального значения, равного H_max (X)= =logm_X, для передачи того же количества информации I тре­буется минимальное количество букв, равное п₀=I/Н_max(X).

Отсюда I=пН_И=п₀Н_max или . Учитывая пос-леднее равенство, выражение для. избыточности можно запи­сать в виде

.

Таким образом, избыточность показывает, какая часть букв в слове не загружена информацией.

Пример 1. Определить избыточность источника, если он вырабатывает статистически независимую последовательность из единиц и нулей соответственно с вероятностями, равными р=0,3 и q=0,7.

Решение. Поскольку символы в последовательности стати­стически независимы, то производительность источника

.

Максимально возможная производительность источника , посколькуm_X=2. При этом символы 1 и 0 должны вырабатываться с равными вероятностями (p=q= =0,5). Отсюда

.

Пример 2. Определить избыточность стационарного мар­ковского источника, алфавит которого состоит из двух символов: 0 и 1. Вырабатываемая источником последо-вательность представляет собой простую цепь Маркова. Заданы следую­щие значения условных вероятностей

Решение. Безусловную вероятность того, что (k+1)-м символом последовательности будет нуль, по формуле полной вероятности можно представить в виде

.

В правую часть неравенства входит вероятность p_k(0) того, что k-ì символом последовательности будет нуль. В силу стационарности источника . Подставив в равенство значения p(0|0) и р(0|1), получим

р(0)=0,125 , р(1)=1— р(0)=0,875.

Производительность источника

а избыточность источника

,

где H_max(X)=1.

Когда отношение v/n стремится к нулю, при неограниченном возрастании п марковский источник вырабатывает типичные последовательности, количество которых или бо­лее приближенно .