Лекция № 11

Тема: Представление информации в цифровых автоматах

1. Позиционные и непозиционные системы счисления

Системой счисления называется совокупность приемов и правил для записи чисел цифровыми знаками. Любая предназначенная для практического применения система счисления должна обеспечивать:

• возможность представления любого числа в рассматриваемом диапазоне величин;

• единственность представления (каждой комбинации символов должна соответствовать одна и только одна величина);

• простоту оперирования числами.

Все системы представления чисел делят на позиционные и непозиционные.

Непозиционная система счисления– система, для которой значение символа не зависит от его положения в числе.

Для их образования используют в основном операции сложения и вычитания. Например, система с одним символом-палочкой встречалась у многих народов. Для изображения какого-то числа в этой системе нужно записать количество палочек, равное данному числу. Эта система неэффективна, так как запись числа получается длинной. Другим примером непозиционной системы счисления является римская система, использующая набор следующих символов: I,V,X,L,C,D,Mи т. д. В этой системе существует отклонение от правила независимости значения цифры от положения в числе. В числахLXиXLсимволXпринимает два различных значения: +10 – в первом случае и –10 – во втором случае.

Позиционная система счисления– система, в которой значение символа определяется его положением в числе: один и тот же знак принимает различное значение. Например, в десятичном числе 222 первая цифра справа означает две единицы, соседняя с ней – два десятка, а левая – две сотни.

Любая позиционная система характеризуется основанием. Основание (базис) позиционной системы счисления – количество знаков или символов, используемых для изображения числа в данной системе.

Для позиционной системы счисления справедливо равенство

(1)

где A_(q)– произвольное число, записанное в системе счисления с основаниемq;a_i– коэффициенты ряда (цифры системы счисления);n,m– количество целых и дробных разрядов.

На практике используют сокращенную запись чисел:

(2)

Например:

а) в двоичной системе (q=2)

11010.101₂= 1 · 2⁴+ 1 · 2³+ 0 · 2²+ 1 · 2¹+ 0 · 2⁰+ 1 · 2^-1+ 0 · 2^-2+ 1 · 2^-3;

б) в троичной системе (q=3)

22120.212₃= 2 · 3⁴+ 2 · 3³+ 1 · 3²+ 2 · 3¹+ 0 · 3⁰+ 2 · 3^-1+ 1 · 3^-2+ 2 · 3^-3;

в) в шестнадцатиричной системе (q=16)

A3F.1CD₁₆ = A · 16² + 3 · 16¹ + F · 16⁰ + 1 · 16^-1 + C · 16^-2 + D · 16^-3.

2. Методы перевода чисел

Числа в разных системах счисления можно представить следующим образом:

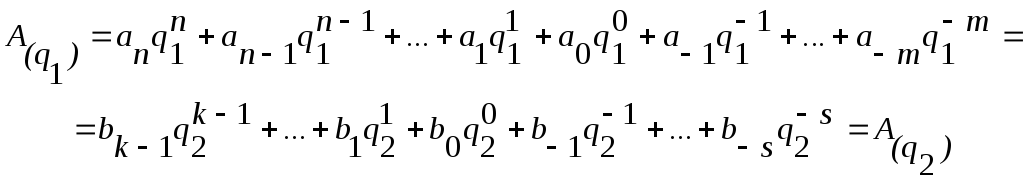
где

Значит, в общем виде задачу перевода числа из системы счисления с основанием q₁в систему счисления с основаниемq₂можно представить как задачу определения коэффициентовb_jнового ряда, изображающего число в системе с основаниемq₂. В такой постановке задачу перевода можно решить подбором коэффициентовb_j.

Перевод чисел делением на основание новой системы

Перевод целых чисел осуществляется делением на основание q₂новой системы счисления, правильных дробей – умножением на основаниеq₂. Действия деления и умножения выполняются по правиламq₁-арифметики. Перевод неправильных дробей осуществляется раздельно по указанным правилам, результат записывается в виде новой дроби в системе с основаниемq₂.

Пример 1. Перевести десятичное число A= 61₁₀в систему счисления сq= 2.

61| 2

60 30| 2

b₀ = 1 30 15| 2

b₁ = 0 14 7| 2

b₂ = 1 6 3| 2

b₃= 1 21 =b₅

b₄ = 1

Ответ: 61₁₀= 111101₂.

Табличный метод перевода

В простейшем виде табличный метод заключается в следующем: имеется таблица всех чисел одной системы с соответствующими эквивалентами из другой системы; задача перевода сводится к нахождению соответствующей строки таблицы и выбору из нее эквивалента. Такая таблица очень громоздка и требует большой емкости памяти для хранения.

Другой вид табличного метода заключается в том, что имеются таблицы эквивалентов в каждой системе только для цифр этих систем и степеней основания (положительных и отрицательных); задача перевода сводится к тому, что в выражение ряда (1) для исходной системы счисления надо поставить эквиваленты из новой системы для всех цифр и степеней основания и произвести соответствующие действия (умножения и сложения) по правилам q₂-арифметики. полученный результат этих действий будет изображать число в новой системе счисления.

Пример 2.Перевести десятичное числоA= 113 в двоичную систему счисления, используя таблицу эквивалентов цифр и степеней основания

(q₂ = 2).

Таблица 1 – Таблица эквивалентов

Десятичное число	Двоичное число
100	0001
101	1010
102	110 0100

Решение. Подставив значения двоичных эквивалентов десятичных цифр и степеней основания в (3), получим

A = 113 = 1 · 10² + 1 · 10¹ + 3 · 10⁰ = 001 · 1100100 + 0001 · 1010 + 0011 · 0001 = 1110001₂.

Ответ: 1110001₂.

3. Форматы представления чисел с фиксированной плавающей запятой

Число 0,028 можно записать так: 28·10^-3, или 2,8·10^-2, или 0,03 (с округлением) и т. д. В компьютере используются две формы представления чисел.

Представление чисел с фиксированной запятой (точкой). Оно характеризуется тем, что положение разрядов числа в машинном изображении остается всегда постоянным независимо от величины самого числа.

Число А можно представить в виде

A=[A]_фK_A,

где [A]_ф– машинное изображение числа в формате с фиксированной запятой, значение которого лежит в пределах

-1 < [A]_ф < 1;

K_A– масштабный коэффициент, выбирается так, чтобы сохранить соответствие разрадов всех чисел, которыми оперирует компьютер.

Формат (разрядная сетка) машинного изображения чисел с фиксированной запятой разбивается на знаковую часть и поле числа. В знаковую часть записывается информация о знаке числа: 0, если A≥0; 1, еслиA<0.

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

№ разряда