Continuity Equation

When a fluid is in motion, it must move in such a way that mass is conserved. To see

how mass conservation places restrictions on the velocity field, consider the steady flow

of fluid through a duct (that is, the inlet and outlet flows do not vary with time). The inflow and outflow are

one-dimensional, so that the velocity V and density \rho are constant over the

area A (figure 14).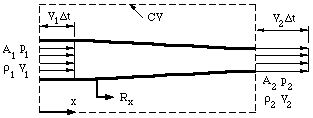

Figure 14. One-dimensional duct showing control volume.

Now we apply the principle of mass conservation. Since there is no flow through the

side walls of the duct, what mass comes in over A_1 goes out of A_2, (the flow

is steady so that there is no mass accumulation). Over a short time interval \Delta t,

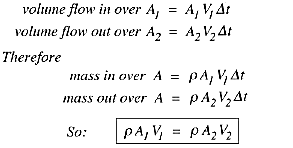
This is a statement of the principle of mass

conservation for a steady, one-dimensional flow, with one inlet and one outlet. This equation is called the

continuity equation for steady one-dimensional flow. For a steady flow through a control volume with

many inlets and outlets, the net mass flow must be zero, where inflows are negative and outflows are positive.

Streamlines and Streamtubes

A streamline is a line that is

tangential to the instantaneous velocity direction (velocity is a vector, and

it has a magnitude and a direction). To visualize this in a flow, we

could imagine the motion of a small marked element of fluid. For example, we could mark a

drop of water with fluorescent dye and illuminate it using a laser so

that it fluoresces. If we took a short exposure photograph as the drop moves

according to the local velocity field (where the exposure needs to be short compared to the

time it takes for the velocity to change appreciably), we would see a short streak, with a

length

V \Delta t, and with a direction tangential to the instantaneous velocity direction. If we

mark many drops of water in this way, the streamlines in the flow will become visible. Since the velocity at any point in the flow has a single value

(the flow cannot go in more than one direction at the same time), streamlines cannot

cross. except at points where the velocity magnitude is zero, such as at a stagnation point.

There are other ways to make the flow visible. For example, we can trace out the path

followed by our fluorescent drop using a long-exposure photograph. This line is called a

pathline, and it is similar to what you see when you take a long-exposure photograph

of car lights on a freeway at night. It is possible for pathlines to cross, as you can

imagine from the freeway analogy: as a car changes lanes, the pathline traced out by its

lights might cross another pathline traced out by an adjoining vehicle at a different

time.

Another way to visualize flow patterns is by streaklines. A streakline is the

line traced out by all the particles that passed through a particular point at some earlier

time. For instance, if we issued fluorescent dye continuously from a fixed point, the dye

makes up a streakline as it passes downstream. To continue the freeway analogy, it is the

line made up of the lights on all the vehicles that passed through the same toll booth.

If they all follow the same path (a steady flow), a single line results, but if they follow

different paths (unsteady flow), it is possible for the line to cross over itself. In

unsteady flow, streamlines, pathlines and streaklines are all different, but in steady flow, streamlines, pathlines

and streaklines are identical. Bernoulli's Equation

equation states that,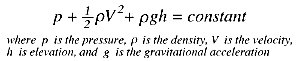

where

points 1 and 2 lie on a streamline,

the fluid has constant density,

the flow is steady, and

there is no friction.

Although these restrictions sound severe, the Bernoulli equation is very useful, partly

because it is very simple to use and partly because it can give great

insight into the balance between pressure, velocity and elevation.

How useful is Bernoulli's equation? How restrictive are the

assumptions governing its use? Here we give some examples.

Pressure/velocity variation

Consider the steady, flow of a constant density fluid

in a converging

duct, without losses due to friction (figure 14). The flow

therefore satisfies all the restrictions governing the use of Bernoulli's equation.

Upstream and downstream of the contraction we make the one-dimensional assumption that the

velocity is constant over the inlet and outlet areas and parallel.

Figure 14. One-dimensional duct showing control volume.

When streamlines are parallel the pressure is constant

across them, except for hydrostatic head differences (if the pressure was higher in the middle of the duct, for example, we would expect the streamlines to diverge, and vice versa). If we ignore gravity, then the

pressures over the inlet and outlet areas are constant. Along a

streamline on the centerline, the Bernoulli equation and the

one-dimensional continuity equation give, respectively,

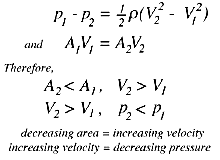
These two observations provide an intuitive guide for analyzing fluid flows, even when the

flow is not one-dimensional. For example, when fluid passes over a solid body, the

streamlines get closer together, the flow velocity increases, and the pressure

decreases. Airfoils are designed so that the flow over the top surface is faster than over

the bottom surface, and therefore the average pressure over the top surface is less than

the average pressure over the bottom surface, and a resultant force due to this pressure

difference is produced. This is the source of lift on an airfoil. Lift is defined as the

force acting on an airfoil due to its motion, in a direction normal to the direction of

motion. Likewise, drag on an airfoil is defined as the force acting on an airfoil due to

its motion, along the direction of motion.

An easy demonstration of the lift produced by an airstream requires a piece of

notebook paper and two books of about equal thickness. Place the books four to five inches

apart, and cover the gap with the paper. When you blow through the passage made by the

books and the paper, what do you see? Why?

Two more examples:

Example 1

A table tennis ball placed in a

vertical air jet becomes suspended in the jet, and it is very stable to small perturbations

in any direction. Push the ball down, and it springs back to its equilibrium position;

push it sideways, and it rapidly returns to its original position in the center of the jet.

In the vertical direction, the weight of the ball is balanced by a force due to pressure

differences: the pressure over the rear half of the sphere is lower than over the front

half because of losses that occur in the wake (large eddies form in the wake that dissipate

a lot of flow energy). To understand the balance of forces in the horizontal direction, you need to know that the jet has its maximum velocity in the center, and the velocity of

the jet decreases towards its edges. The ball position is stable because if the ball

moves sideways, its outer side moves into a region of lower velocity and higher pressure,

whereas its inner side moves closer to the center where the velocity is higher and the

pressure is lower. The differences in pressure tend to move the ball back towards the

center.

Example 3

Suppose a ball is spinning clockwise as it travels through the air from left to right

The forces acting on the spinning ball would be the same if it

was placed in a stream of air moving from right to left, as

shown in figure 15.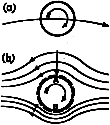

Figure 15. Spinning ball in an airflow.

A thin layer of air (a boundary layer) is forced to spin with the ball

because of viscous friction. At A the motion due to spin is opposite to that of the

air stream, and therefore near A there is a region of low velocity where the pressure

is close to atmospheric. At B, the direction of motion of the boundary layer is the

same as that of the external air stream, and since the velocities add, the pressure in

this region is below atmospheric. The ball experiences a force acting from A to B,

causing its path to curve. If the spin was counterclockwise, the path would

have the opposite curvature. The appearance of a side force on a spinning sphere or

cylinder is called the Magnus effect, and it well known

to all participants in ball sports, especially baseball, cricket and tennis players.

Stagnation pressure and dynamic pressure

Bernoulli's equation leads to some

interesting conclusions regarding the variation of pressure along a streamline.

Consider a steady flow impinging on a perpendicular plate

(figure 16).

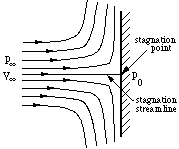
Figure 16. Stagnation point flow.

There is one streamline that

divides the flow in half: above this streamline all the flow goes over the plate, and

below this streamline all the flow goes under the plate. Along this dividing streamline,

the fluid moves towards the plate. Since the flow cannot pass through the plate, the

fluid must come to rest at the point where it meets the plate. In other words, it

``stagnates.'' The fluid along the dividing, or ``stagnation streamline'' slows down

and eventually comes to rest without deflection at the stagnation point.

Bernoulli's equation along the stagnation streamline gives

where the point e is far upstream and point

0 is at the stagnation point. Since

the velocity at the stagnation point is zero,

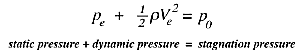
The stagnation or total pressure, p_0, is the

pressure measured at the point where the fluid comes to rest. It is the highest pressure

found anywhere in the flowfield, and it occurs at the stagnation point. It is the sum of

the static pressure

(p_0), and the dynamic pressure

measured far upstream. It is called

the dynamic pressure because it arises from the motion of the fluid.

The dynamic pressure is not really a pressure at all: it is simply a convenient name

for the quantity (half the density times the velocity squared), which represents the decrease

in the pressure due to the velocity of the fluid.

We can also express the pressure anywhere in the flow in the form of a

non-dimensional pressure coefficient C_p, where

At the stagnation point C_p = 1, which is its maximum value. In the freestream, far from

the plate, C_p = 0.

Pitot tube

One of the most immediate applications of

Bernoulli's equation is in the measurement of velocity with a Pitot-tube. The Pitot

tube (named after the French scientist Pitot) is one of the simplest and most useful instruments ever devised.

It simply consists of a tube bent at right angles (figure 17).

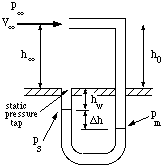
Figure 17. Pitot tube in a wind tunnel.

By pointing the tube directly

upstream into the flow and measuring the difference between the pressure sensed by the

Pitot tube and the pressure of the surrounding air flow, it can give a very accurate

measure of the velocity. In fact, it is probably the most accurate method available for

measuring flow velocity on a routine basis, and accuracies better than 1% are easily

possible. Bernoulli's equation along the streamline that

begins far upstream of the tube and comes to rest in the mouth of the Pitot tube

shows the Pitot tube measures the stagnation pressure in the flow.

Therefore, to find the velocity

V_e, we need to know the density of air, and the

pressure difference

(p_0 - p_e). The density can be found from standard tables if the temperature and

the pressure are known. The pressure difference

is usually found indirectly by using a ``static pressure tapping''

located on the wall of the wind tunnel, or on the surface of the model

. Transition and Turbulence

This section was adapted from The Engine and the Atmosphere: An

Introduction to Engineering by Z. Warhaft, Cambridge University Press, 1997.

How many times a day do we turn on a faucet? Do it now. First very slowly,

and you will see glassy, orderly flow. If there is no wind or other disturbance,

nothing will change. This is called laminar flow. A photo taken now will be

identical to one taken half an hour later. Such a flow is deterministic;

information about its future behavior is completely determined by specification

of the flow at an earlier time. Now open the faucet to full on, or better still

open a fire hydrant, or watch a smoke stack. Here, for this faster or larger

scale motion, the flow pattern is changing all the time. Although its average

motion is in one direction (sideways for the fire-hydrant, up for the smoke

stack), within the flow there are irregularities everywhere. For example if you

could train your eyes on a small speck of dust it would certainly move along but

it would jitter as well, sometimes darting to one side, or up or down. Turbulent

flow while proceeding in a particular direction, like laminar flow, has the

added complexity of random velocity fluctuations. The flow patterns never repeat

themselves. To convince yourself of this watch a smoke stack for a few minutes.

Fluid flow that is slow tends to be laminar. As it speeds up a transition

occurs and it crinkles up into complicated, random turbulent flow. But even

slow flow coming from a large orifice can be turbulent; this is the case with

smoke stacks. Engineers and scientists don't like to say ``fast'' or ``slow''

or ``small'' and ``big'' since there is no reference. Small compared to what?

Big compared to what? Since turbulence is altogether a different type of

fluid flow to laminar flow, it is desirable to be able to quantify under what conditions it occurs.

Let us re-do the faucet experiment in a more systematic way. We have shown

that as the speed, V, increases, transition to turbulence will occur.

Now, instead of using water in your pipes, replace it with honey. Assuming

you could provide a large enough pressure, even for fast flow the motion

would remain laminar. If you do not wish to do this experiment, stir a

spoon rapidly in a cup of water and then at the same speed (working hard)

in a cup of honey. Honey has a higher viscosity than water and the viscosity resists transition to turbulence: while the water is turbulent, the honey remains

laminar at the same speed. Finally, put a nozzle on your tap and constrict

the water flow into a fine glass capillary tube. Here too the flow can be made

to go quite fast without it becoming turbulent. Our experiments suggest

that laminar flow occurs for low speeds, small diameters, low densities and high

viscosities, while turbulent flows occur for the opposite conditions: high speeds, large

diameters, high densities and low viscosities. Now viscosity is a measurable fluid property

(as is its density, temperature, etc.). We will discuss it more in a moment, but we often

use the ``kinematic viscosity,'' which is the viscosity divided by the density. Its unit is

m^2/s. Notice its dimensions are the same as a length multiplied by a velocity. If the

fluid speed is V (m/s), the orifice diameter is d (m) then we can write the

following dimensionless ratio

Re is the Reynolds number, named after Osborne Reynolds who

did systematic experiments, of a similar type to those described above, one

hundred years ago. Notice that if V or d (or both) are small and the viscosity is

large, Re will be small. For this case the flow will be laminar. Increase d

or V or decrease the viscosity, and Re will increase. Reynolds found that for flow

in a pipe it did not matter which of the three particular parameters he varied

in this dimensionless group: as long as Re was less than approximately 2300, the flow was laminar. Above this value, turbulence would invariably occur.

This is a general result since it allows us to vary the type of fluid, flow

speed and pipe diameter without having to use the words ``large'' or ``fast'',

etc. Moreover, since Re is dimensionless, it does not matter which system

of units are used (S.I., Engineering, etc.) so long as they are the same

throughout. We can now talk of high Reynolds number flow or low Reynolds number

pipe flow, knowing that in this context low means somewhat less than 2000. The

kinematic viscosity of water is approximately 10^{-6} m^2/s (that of honey is about

10^{-3} m^2/s, 1000 times greater than that of water). Thus if the pipe

diameter is say 1 cm, the speed at which the Reynolds number is 2000, is 0.2 m/s or approximately 0.4 mph, a rather

slow speed. Water undergoes transition to turbulence at low speeds. Most of the water flows we see,

such as in streams and rivers, are indeed turbulent.

Air too is a fluid, its viscosity, \nu, is approximately 10^{-3} m^2/s.

This is a higher viscosity than that of water. This rather counter-intuitive fact is

due to the great differences in density of the two fluids. Water has a density

of approximately 1000 kg/m^3; the air density is 1.2 \, kg/m^3. Thus

part of the ``viscous feeling'' we have when we pull our fingers through

water is really due to inertia --- we are having to move the water away from our

hands and this also provides resistance. For this reason we need to remember the difference between the dynamic viscosity and the kinematic viscosity. The dynamic viscosity of water is approximately

10^{-3} kg/(m s) while that of air is 1.2 \times 10^{-5} kg/(m s). Thus the

dynamic viscosity of water is higher than that of air, in keeping with our

intuitive notion.

While the transition from laminar to turbulent flow occurs at a Reynolds

number of approximately 2300 in a pipe, the precise value depends on whether

any small disturbances are present. If the experiment is very carefully

arranged so that the pipe is very smooth and there are no disturbances to the

velocity and so on, higher values of Re can be obtained with the flow still in

a laminar state. However, if Re is less than 2300, the flow will be laminar

even if it is disturbed. Thus 2300 is the value the Re below which turbulence

will not occur in a pipe. Moreover, if the flow has a different geometry, such

as flow in a square duct, or over a turbine blade, transition will occur at

different values of Re. The essential point is that flows become turbulent at

high Reynolds numbers where ``high'' means much greater than unity.

Air motion is invariably turbulent. Consider a smokestack (which to a

first approximation is mostly air). If its diameter is say 3 m, then V

must be less than 6.6 mm/s (0.015 mph) for it to be laminar! There is

no such thing as a laminar smokestack. Clouds too are usually turbulent. Here we

determine the Reynolds number using an approximate characteristic dimension of

the cloud such as its height or width. Assuming the cloud dimension is say 500 m, and its

characteristic internal motion is say 5 m/s, then taking the kinematic viscosity to be 10^{-5} m^2/s (it is approximately the same for water vapor as it is for air), the

Re = (500 x 5)/10^{-5} = 2.5 x 10^8. A high value indeed. No wonder

cumulus clouds always have a random, puffy looking turbulent

structure (see also the plume generated by Mt. St. Helens in the picture above).

Turbulent Flow

When the flow is

turbulent, the flow contains eddying motions of all sizes, and a large part of the

mechanical energy in the flow goes into the formation of these eddies which eventually

dissipate their energy as heat. As a result, at a given Reynolds number, the drag of a

turbulent flow is higher than the drag of a laminar flow. Also, turbulent flow is

affected by surface roughness, so that increasing roughness increases the drag.

Transition to turbulence can occur over a range of Reynolds numbers, depending on many

factors, including the level surface roughness, heat transfer, vibration, noise, and

other disturbances. To understand why this is so, and to appreciate the role of the

Reynolds number in governing the stability of the flow, it is helpful to think in terms

of a spring-damper system such as the suspension system of a car. Driving along a bumpy road, the springs act to reduce the movement experienced by the passengers. If there

were no shock absorbers, however, there would be no damping of the motion, and the car

would continue to oscillate long after the bump has been left behind. So the shock

absorbers, through a viscous damping action, dissipate the energy in the oscillations and

reduce the amplitude of the oscillations. If the viscous action is strong enough, the

oscillations will die out very quickly, and the passengers can proceed smoothly. If

the shock absorbers are not in good shape, the oscillations may not die out. The

oscillations can actually grow if the excitation frequency is in the right range, and the

system can experience resonance. The car becomes unstable, and it is then virtually

uncontrollable.

In fluid flow, we often interpret the Reynolds number as the ratio of the inertia force

(that is, the force given by mass x acceleration) to the viscous force. At low Reynolds numbers, therefore, the viscous

force is large compared to the inertia force, and the flow behaves in some ways like a

car with a good suspension system. Small disturbances in the velocity field, created

perhaps by small roughness elements on the surface, or pressure perturbations from

external sources such as vibrations in the surface or strong sound waves, will be

damped out and not allowed to grow. This is the case for pipe flow at

Reynolds numbers less than the critical value of 2300 (based on pipe diamter and average velocity), and for boundary layers with a Reynolds number less than about 200,000 (based on distance from the origin of the layer and the freestream velocity). As the Reynolds number

increases, however, the viscous damping action becomes comparatively less, and at some

point it becomes possible for small perturbations to grow, just as in the case of a car

with poor shock absorbers. The flow can become unstable, and it can experience

transition to a turbulent state where large variations in the velocity field can be

maintained. If the disturbances are very small, as in the case where the surface is very

smooth, or if the wavelength of the disturbance is not near the point of resonance, the

transition to turbulence will occur at a higher Reynolds number than the critical value. So the point of transition does not correspond to a single Reynolds number, and

it is possible to delay transition to relatively large values by controlling the

disturbance environment. At very high Reynolds numbers, however, it is not

possible to maintain laminar flow since under these conditions even minute disturbances will

be amplified into turbulence.

Turbulent flow is characterized by unsteady eddying motions that are in constant motion

with respect to each other. At any point in the flow, the eddies produce fluctuations

in the flow velocity and pressure. If we were to measure the streamwise velocity

in turbulent pipe flow, we would see a variation in time as shown in

figure 14.

Figure 14. Velocity at a point in a turbulent flow as a function of time.

We see that the velocity has a time-averaged value \bar U

and a fluctuating value u', so that \bar U is not a function of

time, but u' is.

The eddies interact with each other as they move around, and they can exchange momentum

and energy. For example, an eddy that is near the centerline of the pipe (and therefore

has a relatively high velocity), may move towards the wall and interact with eddies near

the wall (which typically have lower velocities). As they mix, momentum differences are

smoothed out. This process is superficially similar to the action of viscosity which

tends to smooth out momentum gradients by molecular interactions, and turbulent flows are sometimes said to have an equivalent eddy viscosity. Because turbulent mixing is

such an effective transport process, the eddy viscosity is typically several

orders of magnitude larger than the molecular viscosity. The important point is that

turbulent flows are very effective at mixing: the eddying motions can very quickly

transport momentum, energy and heat from one place to another. As a result, velocity differences get smoothed out more effectively than in a laminar flow, and the

time-averaged velocity profile in a turbulent flow is much more uniform than in

a laminar flow (see figure 4).

As a result of this mixing, the velocity gradient at the wall is higher than that seen

in a laminar flow at the same Reynolds number, so that the shear stress at the wall is

correspondingly larger. This observation is in agreement with the fact that the losses

in a turbulent flow are much higher than in a laminar flow, and therefore the pressure

drop per unit length will be greater, which is reflected in a larger frictional stress

at the wall.

Return to Aerodynamics of Bicycles Introduction.