Aerodynamics of Bicycles

Introduction: Aerodynamics and Friction Losses

AERODYNAMICS have preoccupied bicycle designers since the early part of this century. The most advanced bicycles today are deployed in track racing. The recently unveiled SB II, or Superbike II, has a lightweight carbon-fiber frame. It also has a range of aerodynamic design elements. Similar features are incorporated into bicycles for some road-racing events in which Lance Armstrong competes.

As the bicycle and its rider move along the road, the air exerts a force that increases sharply with speed. The force is due to friction between the air and the exposed surfaces of the rider and bicycle. At high speed, this drag force can be the most importance source of resistance, and with a wind blowing, it can also lead to significant side forces.

The aerodynamic forces on a vehicle come primarily from differences in pressure and viscous shearing stresses. Pressure and viscosity are basic properties of fluids. There is an important connection between velocity and pressure, expressed in Bernoulli's equation, and between velocity and cross-sectional area, expressed in the continuity equation.

The viscosity of air is very small, but it is not negligible. It is responsible for two types of drag: friction drag, and pressure drag. Frictional drag comes from friction between the air flow and the surfaces exposed to the air flow. This friction arises because air (and other fluids) has viscosity. Viscosity is associated with the ability of a fluid to flow freely. For example, honey has about 100 times the viscosity of water, and it is obvious that the two fluids flow differently, and that it takes much greater force to stir honey than water. The frictional drag also depends on the Reynolds number, because the flow is laminar at low Reynolds numbers, and turbulent at high Reynolds numbers. Pressure drag comes from the the eddying motions that are set up in air by the passage of the rider. This part of the flow is called the wake, and it is similar to the flow left behind a passing boat. It is generally not a strong function of Reynolds number.

There are also two kinds of bodies: streamlined bodies and bluff bodies. A streamlined body looks like a fish, or an airfoil, and the streamlines go smoothly around the body A bluff body looks like a brick, or a cylinder, and the streamlines break away whenever a sharp change in direction occurs. For streamlined bodies, the frictional drag is the dominant source of air resistance. For a bluff body, the dominant source of drag is the pressure drag. It is always true that, for a given frontal area and speed, a streamlined body will have a lower air resistance than a bluff body.

The biggest difference between streamlined and bluff bodies is that in streamlined flow, the regions where losses occur are inside boundary layers and wakes that remain reasonably thin, whereas in bluff bodies, adverse pressure gradients cause the boundary layers to separate, which creates a large wake filled with energetic eddies which dissipate a great deal of mechanical energy and thereby increase the drag.

Parts of a rider and bicycle combination act like a streamlined body, whereas other parts behave like a bluff body. By understanding some basic aerodynamic principles, it becomes possible to identify these components, understand the magnitude of their different contributions to the overall drag, and see how we can reduce the overall drag by altering the shape of the component parts.

Return to top.

. Characteristics of Fluids

The principal difference in the mechanical behavior of fluids compared to solids is that

when a shear

stress is applied to a fluid it experiences a continuing and permanent distortion. Fluids

offer no permanent resistance to

shearing, and they have elastic properties only under direct compression: in contrast to

solids which have all three elastic moduli, fluids possess a bulk modulus only.

Thus, a fluid can be defined unambiguously as a material that deforms continuously

and permanently under the application of a shearing stress, no matter how small.

This

definition does not address the issue of how fast the deformation occurs and as we shall

see later this rate is dependent on many factors including the properties of the fluid

itself. The inability of fluids to resist shearing stress gives them their characteristic

ability to change shape or to flow; their inability to support tension stress is an engineering assumption, but it is a well-justified assumption because such stresses which depend on intermolecular cohesion, are usually extremely small.....

Pressure

Pressure is a stress.

. It is a scalar given by the magnitude of the force per unit

area. In a gas, it is the force per unit area exerted by the change of momentum of the

molecules impinging on the surface. We know from Newton's second law that a net resultant

force will cause a change of momentum in a body, and that the rate of change of momentum is

equal to the applied force. It is a vector relationship, so that even if the magnitude of

the momentum is unchanged, a change in the direction of motion requires a resultant force. The impact of a gas molecule on a solid surface is an elastic impact

so that its momentum magnitude and energy are conserved. However, because its direction of

motion changes on impact, a resultant force must have been exerted by the solid surface on

the gas molecule. Conversely, an equal but opposite force was exerted by the gas molecule

on the solid surface. If we consider a very small area of the

surface of the solid, so that over a short time interval \Delta t very few molecules

collide with the solid over this area, then the force exerted by the gas molecules will

vary sharply with time. When we consider a sufficiently large area, so that the number of

collisions on the surface during the

interval \Delta t is large, then the average force that acts on the solid surface by the molecules is constant. It is this

force, acting on the surface of the solid, that we call the force due to pressure.

In practice, the area

need only be larger than about

10 times (mean free path)^2, so that pressure is a continuum property, by

which we mean to say that for areas of engineering interest, which are almost always much

larger than areas measured in terms of the mean free path, the pressure does not have any measurable statistical fluctuations caused by molecular motions. We can make a distinction

between microscopic properties and the macroscopic properties of a fluid,

where the microscopic properties relate to the behavior on a molecular scale (that is,

scales comparable to the mean free path), and the macroscopic properties pertain to the

behavior on an engineering scale (that is, scales much larger than the mean free path).

Pressure: direction of action

Consider the line of action of the force due to pressure. On a molecular

level, a flat solid surface is never flat. However, it is flat

on average, so that, on average, for each molecule that rebounds with some component

of momentum along the surface, another rebounds with the same component of the momentum in

the opposite direction. The average momentum of the molecules in the direction along

the surface will not change during their impact with the surface. We expect, therefore,

that the average force due to pressure (on a macroscopic scale) acts in a

direction which is purely normal to the surface. Furthermore, since the momentum of the molecules is randomly distributed in space, the

magnitude of the force due to pressure should be independent of the direction of

the surface on which it acts. For instance, a thin flat plate in air will experience a

zero resultant force due to air pressure since the forces due to pressure on its two sides have the same magnitude (the pressure is independent of the orientation of the

surface on which it acts) and they point in opposite directions (each force acts

normal to its own surface). We say that pressure is isotropic (based on Greek

words, meaning equal in all directions, or more accurately in the present case, independent

of direction).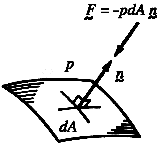

Figure 7. The vector force due to pressure acting on an element of surface.

Pressure: transmission through a fluid

An important property of pressure is that it is transmitted through the fluid.

When an inflated bicycle tube is pressed at one point, for example, the

pressure increases at every other point in the tube. Measurements show that the increase is

the same at every point and equal to the applied pressure. For example, if an extra

pressure of 5 psi were suddenly applied at the tube valve, the pressure would increase

at every point of the tube by exactly this amount. This property of transmitting pressure

undiminished is a well established experimental fact, and it is a property possessed by

all fluids.

The transmission does not occur instantaneously, but at a

rate that depends on the speed of sound in the medium and the shape of the container. The

speed of sound is important because it measures the rate at which pressure disturbances propagate (sound is just a pressure disturbance travelling through a medium). The shape

of the container is important because pressure waves refract and reflect of the

walls of the container and this increases the distance and time the pressure waves need to

travel. This phenomenon should be familiar to anyone who has experienced the imperfect

acoustics of a poorly designed concert hall.

Compressibility in Fluids

All fluids are compressible. However, under some range of conditions, it is often

possible to make the approximation that a fluid is incompressible.

Water, for example, only changes its volume very slightly under extreme pressure.

Gases are much more compressible. The compressibility of air, for example, is part of our

common experience. By blocking off a bicycle pump and pushing down on the handle, we can

easily decrease the volume of the air by 50%, so that its

density increases

by a factor of two (the mass of air is constant). If we assume that the

temperature remains constant (somehow), we know from the perfect gas law,

that the pressure must also increase by a factor of two. If the initial air was at

atmospheric pressure, the pressure will rise by one atmosphere (14.696 psi, or 101,325 Pa). If we assume a pump diameter of 1.25 inch, then a force

of 18.1 lbf will

be required. This is not a large force, so that raising the pressure by two atmospheres

above ambient pressure is easily done.

We call pressures relative to zero

pressure absolute pressure. This is the pressure that appears in the perfect gas

law. Pressures measured relative to

atmospheric pressure are called gauge pressures. The pressure measured

by the most common types of pressure instruments is a gauge pressure since these instruments indicate the pressure relative to atmospheric pressure. A tire gauge, for

instance, measures the pressure in a tire over and above the local atmospheric pressure. A

vacuum gauge, in contrast, will measure the pressure below atmospheric: in common

parlance a ``vacuum'' is any pressure lower than the ambient atmospheric pressure.

Even though gases are much more compressible than liquids (by perhaps a factor of 10^4,

or, four ``orders-of-magnitude''), if the pressures are small the changes in density are

also small. For example, if a 1% change in density is tolerated, then at constant

temperature we can allow a 1% change in pressure. For air this corresponds to a change

in altitude of about 85 meters, so that for changes in height of the order of tall

buildings we can usually neglect the compressibility of air.

The compressibility of gases is also often discussed in terms of the parameter called

the Mach number, which is the ratio of the

fluid velocity to the speed of sound (the speed of sound for air at 20^o C is 343

m/s = 1,126 ft/s = 768 mph).

As we shall see later, when a fluid increases its speed, there is a

corresponding decrease in pressure. If the fluid velocity is small

relative to the speed of sound (that is, the flow has a low Mach number), then the

change in pressure when a fluid increases its velocity from zero to

V is given by

1/2 the density times the velocity squared (in the absence of friction). This quantity

is called the dynamic pressure:

If we again use a 1% level as a tolerable change in density, then if the temperature

remains constant the allowed change in pressure is also equal to 1% (the

process is more likely to be isentropic, but that does not change the argument very much).

This requires

a dynamic pressure less than 1% of the ambient pressure, so that at sea level where the density of air

is about 1.2 kg/m^3 we are limited to velocities less than

40 m/s (132 ft/s or 90 mph), which corresponds to a Mach number of about

0.12. When we consider the flow of air over bicycles, we can always assume that the fluid has a constant density, and that the Mach number is not important.