
- •Часть I основы метрологии 11
- •Международная стандартизация ...196
- •Сертификация продукции ... 197
- •Часть I основы метрологии
- •Глава 1 основных: понятия и определения
- •11 Физическая вг личина
- •1.2. Измерение
- •1.3 Методы измгрений
- •Пример. Измерение массы на равноплечих весах, когда воздействие на весы массы тд полностью уравновешивается массой гирь ти (рис. 1.1, а).
- •1.4. Средства измерений
- •2.1 Систематические погрешности обнаружение и исключени1
- •2.3 Случайные пог решности вероятностное описание результатов и погрешностей
- •Риг,. 2.6 Распредг тени, дискретной случай юи величины
- •В иилу симметрии равномерного распределения медиана величины
- •2.4. Пгямые измерения с многократными наблюдениям и обгаьотка данных
- •И тслючить известные систематические погрешности из резульга тов наблюдений (введением поправки)
- •Вычислить среднее арифметическое исправленных резуль атов на- б;додений принимаемое за результат измерения
- •Вычислить оценку среднего квадратическог о отклонения результатов наблюдения
- •5 Проверить гипотез} о том, что результаты наблюдений принадлежат лормальному распределению
- •6 Вычислит ь доверительны, границы е случайной погрешности результата измерения при заданной веролтности р:
- •7. Вычислить границы суммарной неисключенной систематической погрешности (нсго результата измерении
- •8 Вычислить довери • ельные границы noi решности результата измерения
- •2.5. Пряр1ые однократные измерен! [я с точным оцениванием
- •2.7 Косвенные измерения
- •2.8 Совместные измерения
- •2.9. Оценивание достоверности контроля и погрешности испытаний
- •Часть II
- •Глава 3
- •3.1 Окщие сведении
- •I .Оэффициент амплитуды к.
- •4.1. Элек гронно- тучевой осциллограф
- •Глава 5
- •5.1 Общие сведения
- •5.2 Метод вольтметра амперметр*
- •I шкала разделена на бол! шое число делении в " 50
- •Глава 7
- •71 Общие сведения
- •7.4. Преобразование фазового сдвига го временной интервал
- •Часть I основы метрологии 11
- •Глава 8 измерение параметров электромагнитной совмести лости
- •8Л. Общие сведения
- •8.2 Измерение напрЯjKfhhoc I и электромагни гногополя
- •Пос иЯнн оОличины
- •Часть I основы метрологии 11
- •11.2. П'еханические средства измерения длины
- •3 Под углом а, а оптическая система 4 создаст изображение исследуемой поверхности вместе со спроецированными на нее ш грихами исходного растра в плоское ги рас гра сравнения 5
- •Основы квалиметрии и стандартизации
- •1. Произвести ранжирование однородных объектов по степени выраженности заданного показателя качества
- •12.5 Обработка данных экспертных оценок ka4fctba продукции
- •Часть I основы метрологии 11
- •Глава 13
- •13Л основные понятия и опреце1ения в области стандарт] [зации
- •13 6. Органы и с 7ужбы стандартизации
- •13.7. Государственные и отраслевые системы стандартов на общетехнические нормы тгрмины и определения
- •13.8. Международная стандартизация
- •13.9 Сертификация продукции
х
Рис.
10.1 И: ерение
инерци
иным датчиком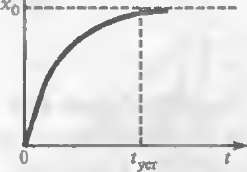
Пос иЯнн оОличины
мических свойств средства измерения и качеств динами ческой norpeir -<ости, о тносятся к частнь м динамическим хараю ерис гикам (постоянная ьремени время успокоения и др )
10.2. IIO1НЫЕ ДИН АМИЧЕСКИ^ XAIАКТЕРИСТ1 ПСИ СРЕДСТВ ИЗМЕРЕНИЯ
Дифференциальное уравнение Цинамиче кии режим широко! о класса средств измерении может быть описан линейным дил ференциальным сравнением с постоянными ко >ффициентами
п d'x(t) m d'x(t\
ХД
- 1;ист
, (1С 1)
i-o dt с
где i, I— порядок производных от r(f)„,u и х(;)ист; At, В,—ко (ффи.'иенты.
В статическом режиме, при хИС1 - const и - < onst уравнег hi (10 1) вы- ччждается в уравнение
хцзм - к^иои
где К = В01А(] — номиг.альный ко >ффициент преобразования средства измерений
Решение диффер нциально* о уравнения позе оляет оценила' ъ дина- „шче жую погрешность и получить исправленный результат измерения, если известны коэффициенты А{ и 3,. Однако коэффициенты уравнения грудно определип расчетчо и экспериментально, поэтому дифференциальное уравнение как динамиче<кая характеристика для оцениваний результа гов и динамических погрешностей не нашло широкого применения на практике.
Передаточная функция Выразив входящие в уравнение (10.1) х(г)ист и х(0изм в операторной форме, запишем уравнение в виде
Часть I основы метрологии 11
/<Д*> = 51
т, =- 58
Д^исп — ХцСп ~ Хисг. 97
Б 115
гО- 99
f = NlT„, 120
U = 1RB, 136
Р -ЩЩ' „0 2, 148
а„= а, + ф- 1), 194
где р — опера ор дифференц. рования didt
Передатинч'щ функцией W(p) называют отношение изображения выходной величины динамической системы к изображению входной величины
11 / ги
Р -ЩЩ' „0 2,
= (А,+А,р*Агр J J Ay )/ ( Д, + Buv + B2p: +.. + Bmp" ).
Как прэчило, передаточные ф* нкции реальных средств измерения удается с достаточной точностью аппроксимировать npot тым выражением (и = 2 - 3, и < т)
гтр-логия стандартизация и технические ирсдства измерений
Если известен закон изменения измеряемой величины x(t)ucrr и переда гочнач функция средства измерения, то опред' гсякл изображение х(р)иж = ЩрЯр)т а затем переходят к оригиналу
Заменив в (10 2) р на /со, получим комплексную (амплитудно-фазовую) характеристику действительная часть которой «яляется амплитудно- частотной характериспзсой А (а), а мнимая — фазо частотной ср(а)).
Переходнан характеригтика Отклик средства измерения на сту пенчатое возмущение единичной высоты назь вается переходной xapai: теристик w h(t)
Реакция ср< детва измерения на воздействие единичного импульса с параметрами х = 0 при t * Оих-ш при г = 0, называется um.v чъсной переходной хиракг.ъеристикои g(t) Математически такой единичныи импульс (дельта-ф* нкция) представляет собой производную от единичной сту!1енчатой функции
Переходная и импульсная переходная характеристики сравнительно просто определяются экспериментально путем подачи на вход средства измерения соответствующего ступенчатого или импульсного входного воздействия и регистрации его выходного сигнагэ
Полные динамические характеристики чинеинь.х аналоговых звень ев святны между собой следующими соотношениями
h(t) = \g(x)dx:
о
g(i) = dh(t)/dr,
W( /со) = Jg{i)t *°'dt = А(а)ем '>;
о
—по
о
При известных h(t) или g(t) выходной сигнал средства измерения на- ходя'г с помощью интеграла Дюамсля
x(t)mu - (d/dt)jx(x)h(t -x)dx
о
I
X (t)m* = f x(x)g(r -l)dx
n
Пример Диф еренциал) юе уравнение термопары имеет вид;
X + *(0юм - СО 3)
dt
где Т— п стояиная времени терм пары. <46
Д намическая система опи лаемая равнение!.. (10.3) назьш-.гся ииерционн м веном первого порядка.
Полныединамическиех&рактериспЖиЛкогс звона пер> - <дная №. к» эристика
i_
Л(0 = 1-е т , импульсная переходная характеристик»
i
g(U - 1/7е т .
переда гочная фу нкция
= 1/(7]в+1): ПО 4)
амллитудно-частотная характерна пса
А(а>) = l/VlWr1 ;
фазо-ч.'стотная -рактеристика
cp(io) = arctgm/'
Реакиия такою инерционного звен< на изменения входного сигнала (температуры) по ступенчатому, линейному и гармоническому законам изо эражена на рис. 10 2.
При ступенчатом входном воздействии (рис. 10 2, а) динамическая погрешность изменяете» по закону
t
Дх(') = - х0 е т
и практ ически ею можно пренебречь. если отечет показаний термопары произ ходить в мэмепты времени t большие, чем (3 ... 4) Т
При линеином изменении измеряемой темпера1 уры
МОисг = bt
Рис.
10.2. Реакци 1
инерциоин т датчика на различные входные
воздействия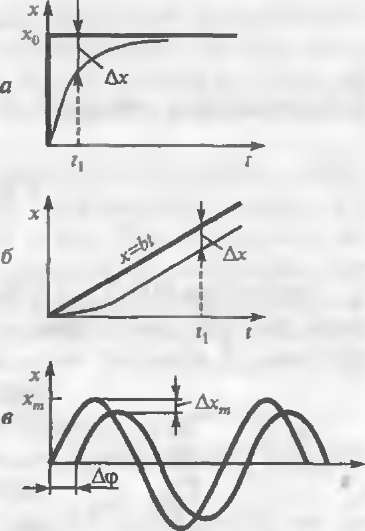
б»
147
При гармоническом изменении измеряемой темг гратуры инерция термопары приводит к уменьшению амплитуды и фа зовому сдвигу сигнала на выходе средства измерения (рис 10.2, в)
10.3. КОРРЕКЦИЯ ДИНАМИЧЕСКИХ ПОГРЕШНОС ГЕЙ
Соврем лшые rexHOjiOi ические процессы осуществляются прп высоких скоростях изменения физических величин пот гежащих измерении! Избежать появления значительных диьами1,еских погрешностей ь таких случаях можно применяя все менее и менее инерционные средства измерений Однако существуют физические пределы уменьшения инерции материальных систем в гом числе и средств измерения, Поэтому одним из способов уменьшения динамических погрешностей является их автоматическая коррею ия путем включения в измерительную цепь керрек тирующа о звена, 'ереда> очная функция которого обратна пере ia точной функции средства измерения
Так, используя в качестне средства измерения термопару с переда точной функцией инерционного звена первого порядка (10 4), при ступенчатом изменении входной величины получаем переходный процесс в виде экспоненты с постоянной времени Т Е^ли же последовательно с термопарой включить кирр'ктирующее звено, передалошая функлия
KOTOpOi о
Ткр н-1 ГЛ) =- 1
Ткр+к
где Тк — постоянная времени корректирующего звена к — коэффи1'иент, то общая передаточная функция системы ст анет W(p) Wk(p) т.е.
Рис.
10..' Корректирующее звено
Тр+\ Тк р + к
Если выполнить у словие Тк - Т, то
Шсбш ■ (10 5 )
* щ
Сравнивая (10 5) и (10.4), видно, что включение корректирующего звена при его правильной настройке (Тк = '[) равноценно уменьшению постоянной времени т ермопары Г в к раз Для инерционно1 о звена
первою порядка н»жная передаточная функция может быть реализована в виде дифферзн цирующего звена (рис 10.3) где Тк = R С, к - =(R, / R2) + 1. Некоторым недостатком такого звена яшяется ослабление в к оаз сигнала на выходе Существую г корректирующие шенья на активных элемен rax, ь которых ослабления сигнала не происходит.
I пива 11
И31\ ПРЕНИЕ ГЕОМ ЕТРИЧЕГКИХ РАЗМЕРОВ
11 1 ОБЩИЕ СВЕДЕНИИ
] Гзготовление изделий машинист роения, микро шектроники опто- электроники и вычислите.1ы ои техники связано с обработкой материалов по заданным размерам, форме и качеству поверхности. При чтом качество изделий контролируется средствами измерения. еомефических )еличин По принятой классификации к iехнике измерения геометрических вели 1ин относят измерения длин и углов, отклонений размеров, формы и расположения поверхностей, параметр" р конусов, резьб и зубчатых колес
Область линеино-yi ловых измерении характеризуется огро™ным числом измерительных задач и объектов измерения Так. измерения отклонений формы и распол эжение поверхностей включаю г в сеоя измерения параметров шероховатости отклонений от параллельности биений. отклонении от перпендикулярности, эксцентриситетов и гп Множество измерител; ных задач возникает и при контроле качества конусов, резьб и зубчатых колес Одно из главных мест в линейно угловых измерениях ганимает измерение длины Диапазон задаваемых линейных размеров здесь простирается от долей микрометра (при измерен ш мик ронеровностеи поверхности) до десятков миллиметров (в электронике) и метров (в маииноефоении).
Методы и .редства измерения геометрических величин подразделяю! на несколько групп, основными из которых являются группы механических и опт ико-механических приборов, рассмотрением которых мы и orpai ичимгя. Но сначала изложим обшие правила выполнения линейных и угловых измерений
При проведении этих измерений на результат измерения значительное влияние оказывают температура окружающей среды, атмосферное давление, влажность, вибрация и т.д. Для того чтобы избежать дополнительных noiрешностей. вызываемых условиями, при которых выполняют измерения, Государственным стандартом установлены следующие требоьания производства линейных и угловых измерений
т емперг-ура окружающей среды 20 °С;
атмосферное давление 101324.72 Па ("СО мм рт ст.);
относительная влажность окру жающего воздуха 58 %;
ускорение свободного падения 9,8 м/с2;
направление линии измерения линейных разм! ров до 1 СО мм наружных поверхностей — вер икальное, в остальных случаях — горизонтальное;
относительная жорость измерения углов, равная нулю
Стандартом также становлено. что р« }ультаты измерений для сопоставимости должны при» питься к укизаннь м нормальнь м зна чиям влияю щи*, величин Пределы до ускаемых с тиюнений от нориальных условии из мерения нормированы в стандартах для разли ных видов измерений
Большое значение для точности линейньх и угловых измерений имеет поддержание стабильной нормальной температуры в зоне измерения Во избежание допо тнительных погрешностей рекомендуется чтобы измеряемые из гелия вы рживали при норма пьной температуре от 2 до 36 ч в зависимости о- и\ массы и допусков на нинеиные размеры Средства же измер< ний до тжны находиться в условиях, соответствующих указанным в стан хартах не менее 24 ч до начала измерений.
Изготовление изделии микро-гектроники оптоэлекфоники и вычислительной техники связано с обработкой материаюв по заданным размерам, фор!.:е и качеству ловерхности Диапазон задаваемых линейных размеров широкий — от долей микрометра (при измерениях микро неровностей поверхности) до десятков миллиметров Измерение геометрических размеров, формы и показателей качества поверхности осуществляется с помощью средств линеиных и угловых измерений Э ги средства подразделяются на несколько групп, основными из которых явля кпея группы механических и оптико механически/ приборов.
