24. Абсолютно упругий удар.

Абсолютно упругий удар — удар, при котором не происходит превращение механической энергии в другие виды энергии.

25. Абсолютно не упругий удар.

А бсолютно не упругий удар — удар, в результате которого после столкновения двух тел, они движутся дальше как единое целое, объединившись.

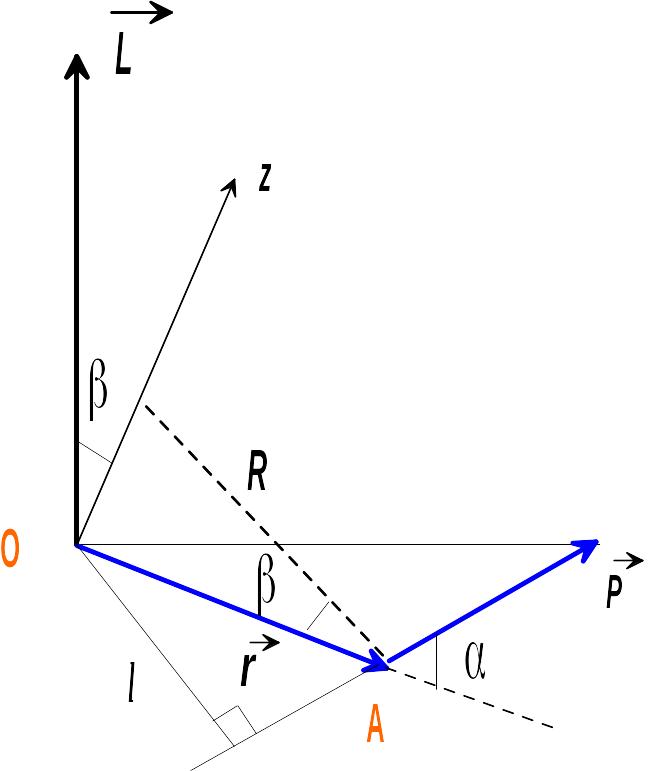
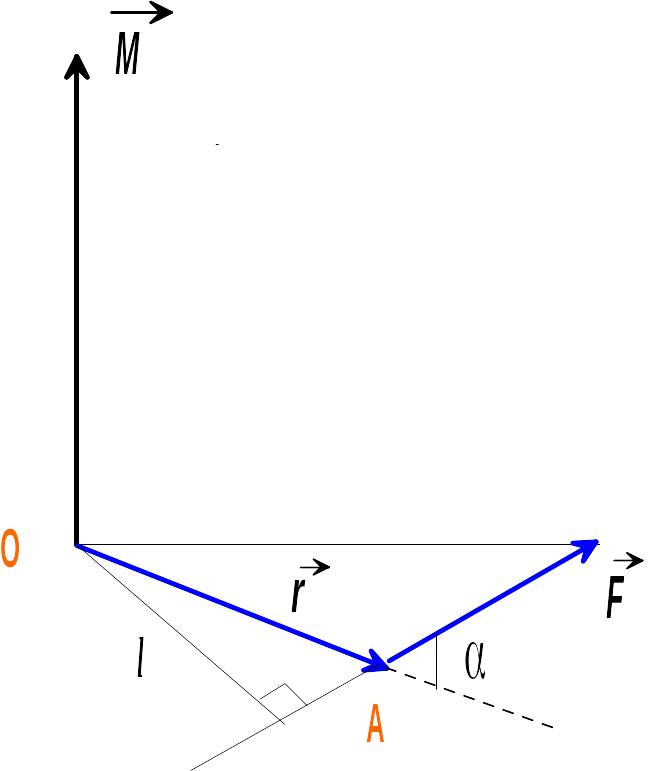
26. Момент силы, момент импульса относительно точки и оси.

Момент силы F относительно неподвижной оси – физ. величина, определяемая векторным произведением радиус-вектора r, проведенного из точки О в точку приложения силы, на силу F: М=[r,F] М- псевдовектор, |M|=|r|∙|F|∙sinα, |F|∙sinα=l – плечо силы. М=М_xi+M_yj+M_zk, М_y=|[r,F]|_y, М_z=|[r,F]|_z , М_x=|[r,F]|_x. Момент силы относительно неподвижной оси – скалярная величина, равная проекции на эту ось вектора М относительно произвольной точки данной оси. Значение М_z не зависит от выбора положения точки О на оси Z. Момент импульса (количество движения) материальной точки относительно неподвижной точки – физ. Величина, определяемая векторным произведением: L=[r,p]=[r,mv]. | r|∙|p|∙sinα=l – плечо импульса. Момент импульса относительно неподвижной оси – скалярная величина, равная проекции на эту ось вектора L относительно произвольной точки на этой оси L=[r,p], для движения по окружности L=[r,mv]. L=rmvsin(v,r)=rmv=ωmR², v перпендикулярно r. Уравнение моментов dL/dT=M. Производная по времени от момента импульса относительно точки равна моменту силы относительно этой точки. Производная по времени от момента импульса относительно оси равна моменту силы относительно этой оси.

27. Уравнение моментов.

dl/dt=M произведение по времени от момента импульса относительно m₀ = моменту силы относительно этой m. Произведение по времени от момента импульса относительно оси равно моменту силы относительно этой оси.

(dl/dt)x=M_x$ (dl/dt)y=M_y; (dl/dt)z=M_z

28. Закон сохранения момента импульса системы материальных точек.

При произвольном движении систем N материальных точек: результирующий момент внутренних сил в соответствии с 3-им законом Ньютона равен 0. Момент импульса замкнутой системы с течением времени не меняется – закон сохранения момента импульса. Закон сохранения момента импульса является прямым следствием законов Ньютона и изотропности пространства – эквивалентности свойств пространства в различных направлениях. Во многих задачах связанных с вращающимися системами угловую скорость вращения и момент импульса можно вычислить с помощью сохранения момента импульса.