
1.3. Закон фурье и коэффициент теплопроводности
Основным законом теплопроводности является Закон Фурье (1822 г.).Он устанавливает взаимосвязь между удельным тепловым потоком и температурным градиентом:
![]()
![]()
![]() (1.4),
(1.4),
где
![]() - множитель пропорциональности, который
называется коэффициентом теплопроводности
и имеет размерность
- множитель пропорциональности, который
называется коэффициентом теплопроводности
и имеет размерность
![]() .
.
Знак минус указывает, что вектор теплового потока направлен в сторону, противоположную температурному градиенту.
Из уравнения (1.4) видно, что коэффициент теплопроводности количественно равен удельному тепловому потоку при температурном градиенте, равном единице - изменение температуры в 10 на единицу длины.
Коэффициент
теплопроводности является важной
теплофизической характеристикой
вещества; чем больше
![]() ,
тем большей теплопроводностью обладает
материал.
,
тем большей теплопроводностью обладает
материал.
Величина коэффициента
теплопроводности зависит от природы
вещества, его структуры, влажности,
наличия примесей, температуры и других
факторов. Наибольший коэффициент
теплопроводности имеют металлы и сплавы
Изотермической поверхностью
7-420
![]()
![]() .
.
Теплоизоляционные, керамические и строительные материалы обладают значительно меньшим коэффициентом теплопроводности - 0,023-2,9 .
В расчетах коэффициент теплопроводности строительных материалов следует принимать по СНиП П-3-79* «Строительная теплотехника».М ГП ЦПП 1995. Значения коэффициента теплопроводности приведены в таблице 1
Таблица 1
Материал |
Коэффициент
теплопроводности
|
Бетон на гравии или щебне из природного камня |
1,45 |
Керамзитобетон при плотности 1200 кг/м3 |
0,46 |
Грунт растительный под зданием |
1,16 |
Кирпичная кладка из обыкновенного глиняного кирпича на легком растворе |
0,76 |
Сложный раствор (песок, цемент, известь) или штукатурка из него |
0,86 |
Алюминий |
221 |
Сталь |
58 |
Чугун |
50 |
Вода (0-100 0С) |
0,55-0,7 |
Лед |
2,5 |
Воздух |
0,024-0,075 |
Снег уплотненный при плотности 350 кг/м3 |
0,35 |
1.4 Теплопроводность
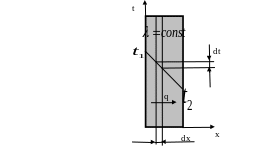
Рис.2.
Р ассмотрим
однослойную, плоскую стенку толщиной
ассмотрим
однослойную, плоскую стенку толщиной
![]() рис.2. Пусть коэффициент теплопроводности
указанной стенки постоянен и равен
.
Температуры на границах стенки
рис.2. Пусть коэффициент теплопроводности
указанной стенки постоянен и равен
.
Температуры на границах стенки
![]() 1
и
1
и
![]() ,
причем
пусть
,
причем
пусть
![]() меньше
.
Тепло
распространяется вдоль оси x.
При этих условиях температурное поле
в стенке будет одномерным и изотермическими
поверхностями будут плоскости,
параллельные поверхностям стенки.
меньше
.
Тепло
распространяется вдоль оси x.
При этих условиях температурное поле
в стенке будет одномерным и изотермическими
поверхностями будут плоскости,
параллельные поверхностям стенки.
Для слоя толщиной
dx
на основании закона Фурье можно написать
следующие уравнения теплопроводности:
q=![]() (1.5)
(1.5)
или
![]() (1.6)
(1.6)
Проинтегрировав данное уравнение, получим
![]() (1.7)
(1.7)
Из уравнения следует, что температура изменяется по толщине стенки по закону линейному закону.
Константа
интегрирования С определяется из условий
на границах стенки: x=0,
то
![]() .
Если x=
.
Если x=![]() ,
то
,
то
![]() и уравнение принимает вид
и уравнение принимает вид
![]() (1.8)
(1.8)
Окончательно получим
![]() (1.9)
(1.9)
Из уравнения видно,
что удельный тепловой поток зависит от
температурного перепада
![]() ,
поэтому можно написать
,
поэтому можно написать
![]() (1.10)
(1.10)
Или
![]() (1.11)
(1.11)
Отношение
![]() называется термическим сопротивлением
стенки. Зная удельный тепловой поток
q,
можно определить общее количество
тепла, переданного в единицу времени
через стенку площадью F,
по формуле
называется термическим сопротивлением
стенки. Зная удельный тепловой поток
q,
можно определить общее количество
тепла, переданного в единицу времени
через стенку площадью F,
по формуле
![]() (1.12).
(1.12).
Из формулы (1.12) видно, что общее количество тепла, переданного через однослойную плоскую стенку, пропорционально удельному тепловому потоку и поверхности стенки F.
Рассмотрим
теплопроводность плоской многослойной
стенки, состоящей из трех слоев,
прилегающих друг к другу. Каждый слой
имеет заданную толщину
![]() и коэффициент теплопроводности
и коэффициент теплопроводности
![]() (рис.3).
(рис.3).

Рис.3
При стационарном
тепловом режиме тепловые потоки через
каждый из слоев стенки одинаковы.
Пользуясь формулой (1.12) для каждого слоя
можно написать
![]()
![]() ;
;
![]() ;
;
![]() .
.
Пренебрегая термическим сопротивлением контакта на границах раздела двух слоев, можно по этим уравнениям определить температуры поверхностей отдельных слоев, а также перепад температур в них:
![]() ;
;
![]() ;
;
![]() .
.
Просуммировав, правые и левые части этих равенств, получим,
![]() ,
,
откуда
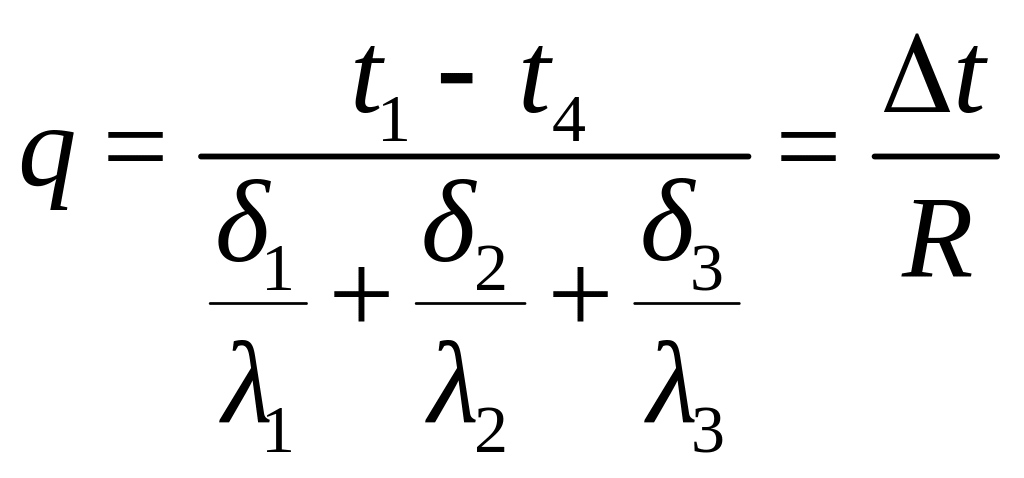 (1.13),
(1.13),
где
![]() - температурный перепад, т.е. разность
температур наружных поверхностей
стенки; R=R1+R2+R3+…Rn
– общее термическое сопротивление
многослойной стенки, равное сумме
термических сопротивлений отдельных
слоев.
- температурный перепад, т.е. разность
температур наружных поверхностей
стенки; R=R1+R2+R3+…Rn
– общее термическое сопротивление
многослойной стенки, равное сумме
термических сопротивлений отдельных
слоев.
Для построения температурного поля многослойной стенки необходимо знать температуру на поверхности каждого слоя в отдельности, которая определится из следующих равенств:
![]() и т.д.
и т.д.
Температурное поле многослойной стенки будет представлять собой ломаную линию.
Тепловой поток через многослойную стенку определяется по формуле
![]() (1.14).
(1.14).
Расчет теплопроводности
однослойной и многослойной цилиндрической
стенки можно производить по формулам
для плоской стенки, если ее толщина
незначительна (![]()
![]() 2) в этом случае,
кривизна стенки незначительно влияет
на величину теплового потока. В этом
случае вместо F
подсчитывается
2) в этом случае,
кривизна стенки незначительно влияет
на величину теплового потока. В этом
случае вместо F
подсчитывается
![]() (1.15)
(1.15)
где dср – средний диаметр цилиндра между наружной и внутренней поверхностями его стенки.
![]() .(1.16)
.(1.16)
Более точное определение среднего диаметра производится по формуле
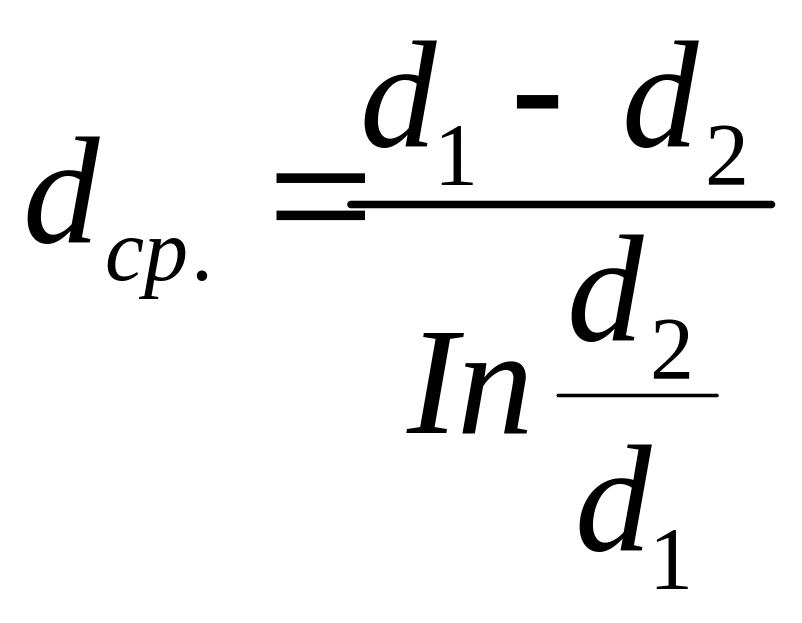 (1.17).
(1.17).
