Коефіцієнт ризику

Стратегії, Sі	Прибуток за варіантами ситуацій					KR
	1	2	3	4	5
S1	17	5	24	10	4	2,06
S2	11	20	14	32	46	0,34
S3	35	5	3	37	2	6,42
S4	15	14	10	30	6	0,32
S5	17	23	20	9	12	0,59
S6	19	4	16	2	1	2,21

Чим менший коефіцієнт ризику (K_R), тим менший ризик. За цим показником найвигіднішою є четверта стратегія.

3. Інтервальна оцінка ефективності кожної стратегії та визначення типу ризику кожної з них.

Для її визначення необхідно розрахувати граничну похибку, яка є абсолютним показником інтегральної оцінки ризику.

Результати розрахунків подано в табл. 9.

Таблиця 9

Граничні похибки

Стратегії, Sі	Прибуток за варіантами ситуацій					∆і
	1	2	3	4	5
S1	17	5	24	10	4	15,61
S2	11	20	14	32	46	25,53
S3	35	5	3	37	2	38,86
S4	15	14	10	30	6	13,42
S5	17	23	20	9	12	10,08
S6	19	4	16	2	1	20,43

, (8)

де t — критерій Стьюдента (таблична величина),  — рівень значущості, або ймовірність, з якою відхиляється рівень граничної похибки.

Додамо граничну похибку до середньої ефективності (математичного сподівання) й дістанемо максимально можливий рівень ефективності із заданою ймовірністю: . У результаті віднімання матимемо мінімально можливе значення очікуваної ефективності: . Чим менше значення граничної похибки (граничного відхилення), тим безпечніша й надійніша стратегія. Такою є п’ята стратегія.

Результати розрахунків подано в табл. 10.

Таблиця 10

Максимально та мінімально можливий рівень ефективності

Стратегії, Sі	Прибуток за варіантами ситуацій					aimax	aimin
	1	2	3	4	5
S1	17	5	24	10	4	29,59	– 1,63
S2	11	20	14	32	46	41,73	– 9,33
S3	35	5	3	37	2	65,37	– 12,35
S4	15	14	10	30	6	28,74	1,90
S5	17	23	20	9	12	27,42	7,26
S6	19	4	16	2	1	34,32	– 6,54

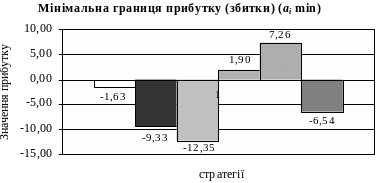
За табл. 10 ми можемо проаналізувати зміни граничних інтервалів ефективності стратегій:

• a_imax характеризує максимальну границю інтервалу ефективності, тобто очікувані прибутки; тут кращою є третя стратегія;

• a_imin характеризує мінімальне значення інтервалу ефективності; коли воно від’ємне, тоді ми можемо бачити розмір утрат; виходячи з цих умов вигіднішою є п’ята стратегія, завдяки своїй не збитковості та найбільшому додатному значенню.

Визначимо ризик на основі розмаху варіації:

. (9)

Результати розрахунків подано в табл. 11.

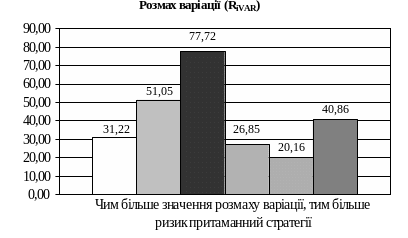
Чим більше розмах варіації, тим більший ризик притаманний стратегії. Отже, п’ята стратегія є найменш ризикованою.

Таблиця 11

Розмах варіації

Стратегії, Sі	Прибуток за варіантами ситуацій					Ri VAR
	1	2	3	4	5
S1	17	5	24	10	4	31,22
S2	11	20	14	32	46	51,05
S3	35	5	3	37	2	77,72
S4	15	14	10	30	6	26,85
S5	17	23	20	9	12	20,16
S6	19	4	16	2	1	40,86

Для того, щоб простежити динаміку стратегій, зобразимо графічно три останні показники.

Встановимо тип ризику через підрахунок відсотка втрат для кожної стратегії (табл. 12).

Таблиця 12

Тип ризику

Стратегії, Sі	Прибуток за варіантами ситуацій					Втрати, %	Тип ризику
	1	2	3	4	5
S1	17	5	24	10	4	– 11,68	Допустимий
S2	11	20	14	32	46	– 57,56	Критичний
S3	35	5	3	37	2	– 46,58	Допустимий
S4	15	14	10	30	6	12,37	Допустимий
S5	17	23	20	9	12	41,86	Допустимий
S6	19	4	16	2	1	– 47,1	Допустимий

Висновок: за вищенаведеною таблицею можна підсумувати таке:

• стратегія S₁ завдасть збитків у розмірі 11,68 %; ця стратегія збиткова, але ризик — допустимий;

• стратегія S₂ завдасть збитків у розмірі 57,56 %; стратегія збиткова, ризик — критичний;

• стратегія S₃ завдасть збитків у розмірі 46,58 %; стратегія збиткова, але ризик — допустимий;

• стратегія S₄ принесе прибуток у розмірі 12,37 %; стратегія є прибутковою.

• стратегія S₅ принесе прибуток у розмірі 41,86 %; це прибуткова стратегія, яка є найвигіднішою за всіма показниками;

• стратегія S₆ завдасть збитків у розмірі 47,1 %; стратегія збиткова, але ризик — допустимий.