3.2. Прийняття рішень щодо ресурсного забезпечення виробництва

Скласти виробничу програму, яка забезпечує одержання максимального обсягу прибутку. У підрозділі виробляється два види продукції (А та Б) у будь-яких комбінаціях. Це означає, що продукція дефіцитна й її збут гарантовано. Але матеріальні й трудові ресурси обмежені.

У задачі не ставиться вимога обов’язкового використання усіх ресурсів. Розрахунок повинен бути виконаний графічним та математичним методами. Вихідні дані надані у таблицях 5,6.

Таблиця 5

Умовне позначення показників

Продукція	Витрати на одиницю продукції			Прибуток на одиницю продукції, грн/од
	Робочого часу, люд-год	Ресурсу 1, кг	Ресурсу 2, кг
А	t1	c1	v1	p1
Б	t2	c2	v2	p2
Разом	T	C	V

Таблиця 6

Вхідні дані про витрати ресурсів і прибуток

Показ-ники	t1	t2	T	c1	c2	C	v1	v2	V	p1	p2
варіант
0	12	8	5800	6	2	3200	-	3	600	20	60
1	5	2	5400	8	5	3000	3	-	350	20	50
2	10	6	6700	4	2,5	3200	4	-	600	60	40
3	7	3	6200	2	5	2800	-	4	300	80	30
4	4,5	2,5	6500	1,8	3,6	2000	5,0	-	1600	9,8	4,2
5	8,2	3,5	8000	5,5	4,2	4000	-	3,7	1500	9,1	4,8
6	8,1	3,4	3000	5,2	2,3	4000	-	3,7	1000	4,7	6,5
7	4	9	7300	7	3	4500	5	-	520	30	60
8	8	5	5900	4	6	2500	-	3	500	30	20
9	10	3	4000	6	4	3000	-	1,5	1000	4,5	6,5

Рекомендації до виконання завдань з обґрунтування рішень щодо ресурсного забезпечення виробництва.

1. Невідомі обсяги випуску продукції приймаються за Х₁ й Х₂.

2. Складаються обмеження щодо використання ресурсів:

3. Складається функція, яка максимізує прибуток:

4. Графічне рішення отримується при побудові відповідних обмежень і функції прибутку

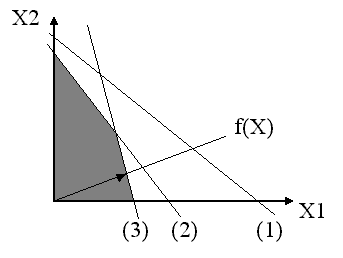
Рис. 1 Графічне рішення системи

5. Для вирішення системи нерівнянь математичним способом необхідно знайти точки перехрещення відповідних прямих. Отримані обсяги необхідно перевірити на обсяг прибутку – підставити значення обсягів до функції прибутку. Ті обсяги, які дають найбільший обсяг прибутку й будуть складати виробничу програму підприємства.