
- •Вопрос №1: (Матрицы. Линейные операции в множестве матриц. Их свойства. Понятие линейного пространства)
- •Линейные операции в множестве матриц.
- •Понятие линейного пространства.
- •Вопрос №2: (Операция умножения матриц. Её свойства. Алгебра квадратных матриц.) Умножение матриц.
- •Алгебра квадратных матриц.
- •Вопрос №3: (Элементарные преобразования строк (столбцов) матрицы. Приведение матрицы к ступенчатому виду с помощью элементарных преобразований.)
- •Приведение матрицы к ступенчатому виду с помощью элементарных преобразований.
- •Вопрос №4: (Перестановки n элементов. Их количество. Инверсии. Четные и нечетные перестановки.)
- •Вопрос №5: (Транспозиция. Изменение четности перестановки при транспозиции любых двух ее элементов. Количество четных и нечетных перестановок n элементов.)
- •Вопрос №6: (Определитель квадратной матрицы. Вывод формулы вычисления определителя второго порядка из общего определения.)
- •Вопрос №7: (Определитель квадратной матрицы. Вывод формулы вычисления определителя третьего порядка из общего определения.)
- •Вопрос №8: (Определитель квадратной матрицы. Вывод формулы вычисления определителя верхней треугольной матрицы.)
- •Вопрос №9: (Определитель квадратной матрицы. Лемма о знаке члена определителя.)
- •Вопрос №14: (Определитель квадратной матрицы. Доказать свойство: Если к одной из строк матрицы добавить другую, умноженную на число, то определитель матрицы не изменится.)
- •Вопрос №15: (Определитель квадратной матрицы. Доказать свойство: Если одна из строк матрицы является линейной комбинацией других ее строк, то определитель матрицы равен нулю.)
- •Вопрос №16: (Как влияют на определитель матрицы элементарные преобразования ее строк. Возможность приведения матрицы к треугольному виду с сохранением ее определителя.)
- •Вопрос №17: (Определитель блочной треугольной матрицы.)
- •Вопрос №18: (Минор и алгебраическое дополнение элемента определителя. Теорема о разложении определителя по строке (столбцу).)
- •Вопрос №19: (Минор и алгебраическое дополнение элемента определителя. Теорема о «фальшивом разложении» определителя по строке (столбцу).)
- •Вопрос №20: (Определитель Вандермонда. Критерий равенства его нулю.)
- •Вопрос №21: (Определитель произведения квадратных матриц.)
- •Что и требовалось доказать. Вопрос №22: (Определение обратной матрицы. Единственность обратной матрицы. Необходимое условие существования обратной матрицы.)
- •Вопрос №23: (Нахождение обратной матрицы с помощью присоединенной матрицы.)
Вопрос №14: (Определитель квадратной матрицы. Доказать свойство: Если к одной из строк матрицы добавить другую, умноженную на число, то определитель матрицы не изменится.)
Определение определителя описывается в вопросе №6!
Доказательство:
Пусть к ![]() -ой
строке матрицы
-ой
строке матрицы ![]() прибавлена
прибавлена ![]() -ая
строка, умноженная на число
-ая
строка, умноженная на число ![]() .
Новую матрицу обозначим
.
Новую матрицу обозначим ![]() .
.
В
матрице
элементы
-ой
строки имеют вид ![]() .
По предложению
14.13
.
По предложению
14.13![]() ,
где
,
где ![]() --
матрица, полученная из матрицы
заменой
-ой
строки на
-ую
строку, умноженную на число
.
--
матрица, полученная из матрицы
заменой
-ой
строки на
-ую
строку, умноженную на число
. ![]() ,
то есть
,
то есть ![]()
Предложение 14.13 Пусть
в матрице
-ая
строка имеет вид ![]() .
Тогда
.
Тогда ![]() ,
где матрица
,
где матрица ![]() получается
из матрицы
заменой
-ой
строки на строку
получается
из матрицы
заменой
-ой
строки на строку ![]() ,
а матрица
,
а матрица ![]() --
заменой
-ой
строки на строку
--
заменой
-ой
строки на строку ![]() .
.
Доказательство. Пусть первая строка матрицы имеет вид . Тогда
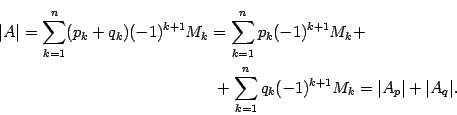
Для
случая ![]() утверждение
доказано.
утверждение
доказано.
Пусть ![]() .
Обозначим через
,
.
Обозначим через
, ![]() ,
, ![]() матрицы
,
,
и
,
в которых поменяли местами первую
и
-ую
строки. По только что доказанному
(для
)
утверждению
матрицы
,
,
и
,
в которых поменяли местами первую
и
-ую
строки. По только что доказанному
(для
)
утверждению ![]() .
По
предложению
14.8
.
По
предложению
14.8 ![]() ,
, ![]() ,
, ![]() .
Следовательно,
.
Следовательно, ![]() .
Умножив обе части последнего равенства
на
.
Умножив обе части последнего равенства
на ![]() ,
получим требуемое утверждение.
,
получим требуемое утверждение.
Вопрос №15: (Определитель квадратной матрицы. Доказать свойство: Если одна из строк матрицы является линейной комбинацией других ее строк, то определитель матрицы равен нулю.)
Определение определителя описывается в вопросе №6!
Доказательство: Определитель исходной матрицы равен сумме определителей матриц, в каждой из которых есть пропорциональные строки. все эти определители равны нулю. Следовательно, и определитель исходной матрицы тоже равен нулю.
det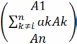
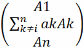 =0
=0
Вопрос №16: (Как влияют на определитель матрицы элементарные преобразования ее строк. Возможность приведения матрицы к треугольному виду с сохранением ее определителя.)
При элементарных преобразованиях ранг матрицы не меняется.


Вопрос №17: (Определитель блочной треугольной матрицы.)
Вычисление определителей блочных матриц:
Пусть
![]() и
и
![]() –
квадратные матрицы (не обязательно
одинакового порядка), а
–
квадратные матрицы (не обязательно
одинакового порядка), а
![]() и
и
![]() – произвольные матрицы, такие, что
блочная матрица
– произвольные матрицы, такие, что
блочная матрица
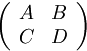 -квадратная
-квадратная
Теорема:
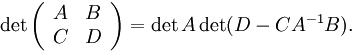
Если все матрицы , , и — одинакового порядка, то
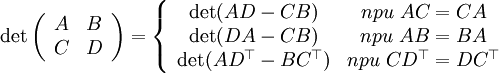
В частном случае когда матрица — первого порядка, приведенная в теореме формула эквивалентна первому шагу метода Гаусса вычисления определителя:

При
условии
![]()
В
частном случае когда матрица
— первого порядка, получаем формулу
для вычисления окаймленного определителя,
т.е. определителя
которую можно сделать универсальной, т.е. действительной и в случае особенной матрицы :
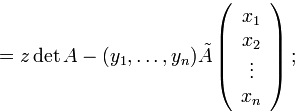
здесь
матрица
![]() — взаимная матрице
— взаимная матрице
Используя представление взаимной матрицы через алгебраические дополнения, получаем:
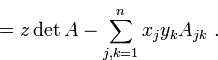
Вопрос №18: (Минор и алгебраическое дополнение элемента определителя. Теорема о разложении определителя по строке (столбцу).)
В определителе порядка n алгебраическим дополнением элемента, стоящего на пересечении k-го столбца и l-й строки, называется определитель порядка (n - 1), получаемый из данного вычеркиванием в нем строки и столбца, на пересечении которых стоит этот элемент, причем к этому определителю присоединяется множитель (-1)k+l, где (k + l) - сумма номеров вычеркнутой строки и столбца. Алгебраическое дополнение элемента, рассматриваемое без множителя (-1)k+l, называется минором этого элемента.
Теорема о разложении определителя по элементам строки.
Определитель матрицы A равен сумме произведений элементов строки на их алгебраические дополнения:
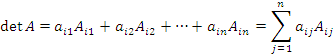
.
Теорема о разложении определителя по элементам столбца.
Определитель матрицы A равен сумме произведений элементов столбца на их алгебраические дополнения:
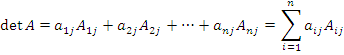
Пусть
![]() — квадратная матрица размера
— квадратная матрица размера
![]() . Пусть также задан некоторый номер
строки
. Пусть также задан некоторый номер
строки
![]() либо
номер столбца
либо
номер столбца
![]() матрицы
матрицы![]() . Тогда определитель
может быть вычислен по следующим
формулам:
. Тогда определитель
может быть вычислен по следующим
формулам:
По строке

По столбцу
![]()
Доказательство:

