Вопрос №4: (Перестановки n элементов. Их количество. Инверсии. Четные и нечетные перестановки.)

Определение:

Перестановкой n элементов называется расположение этих элементов в определенном порядке.

Утверждение 1:

Число перестановок n элементов равно n! = 1*2*3*….*n

Доказательство:

(j₁,j₂,…,j_n)

j₁ – может принимать любые значения от 1,….., n (n – штук)

j₂ – может принимать любые значения из оставшихся (n-1 штук)

Всего элементов: n*(n-1)*(n-2)*….*1 = n!

Определение:

(j₁,….,j_k,….,j_l,….,j_n), j_k и j_l образуют инверсию, если:

1. k < l

2. j_k > j_l

Определение:

Если число инверсий в перестановке четно, то перестановка

называется четной, а если число инверсий в перестановке нечетно, то перестановка называется нечетной.

Вопрос №5: (Транспозиция. Изменение четности перестановки при транспозиции любых двух ее элементов. Количество четных и нечетных перестановок n элементов.)

Определение:

Транспозиция перестановки – это обмен местами двух ее элементов.

α = (2 4 3 1 5)

β = (2 1 3 4 5)

Данный пример показывает нам транспозицию перестановки чисел 1 и 4.

Утверждение: любая транспозиция перестановки изменяет ее четность.

Доказательство: 1) α = (j₁,….,j_k,j_k+1,….,j_n)

β = (j₁,….,j_k+1,j_k,….,j_n)

Транспозиция соседних элементов.

[β] = [α]+1, если j_k < j_k+1 или [β] = [α]-1, если j_k > j_k+1

2) α = (j₁,….,j_k,j_k+1,….,j_k+l+1,….,j_n) - l+1 перестановка j_k с соседними элементами

-> α = (j₁,….,j_k+1,….,j_k+l+1,j_k,….,j_n) - l перестановок j_k+l+1 с соседними элементами -> α = (j₁,….,j_k+l+1,j_k+1,….,j_k,….,j_n) – 2l+1 транспозиций соседних элементов =>

=> 2l+1 раз изменений => четность изменилась

Утверждение:

Число четных и нечетных перестановок из n элементов одинаково и равно (при n ≥ 2)

Вопрос №6: (Определитель квадратной матрицы. Вывод формулы вычисления определителя второго порядка из общего определения.)

Определение: Определителем (детерминантом)  – го порядка или определителем (детерминантом) квадратной матрицы  – го порядка называют алгебраическую сумму всех членов определителя данной матрицы, взятых со своими знаками.

Обозначение:

,

где суммирование ведется по всем перестановкам столбцов.

Вывод формулы вычисления определителя второго порядка из общего определения:

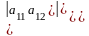
Вопрос №7: (Определитель квадратной матрицы. Вывод формулы вычисления определителя третьего порядка из общего определения.)

Определение определителя описывается в вопросе №6!

Вывод формулы вычисления определителя третьего порядка из общего определения:

Вопрос №8: (Определитель квадратной матрицы. Вывод формулы вычисления определителя верхней треугольной матрицы.)

Определение определителя описывается в вопросе №6!

Вопрос №9: (Определитель квадратной матрицы. Лемма о знаке члена определителя.)

Определение определителя описывается в вопросе №6!

Лемма о знаке члена определителя:

Пусть дана квадратная матрица  – го порядка:

.

Определение:

Произведение   элементов матрицы А, взятых по одному из каждой строки и каждого столбца называют членом определителя матрицы А.

Обозначение: .

Здесь первый индекс обозначает номер строки, из которой взят элемент, второй индекс  , он в свою очередь имеет нижний индекс  , обозначает номер столбца, из которой взят элемент и набор вторых индексов образует перестановку    множества  .

Т.к. число всех перестановок множества   равно  , то существует ровно   членов определителя.

Каждый член определителя снабдим знаком плюс или минус, в зависимости от четности или нечетности перестановки вторых индексов. Это можно сделать с помощью множителя  , который равен 1, если перестановка   четная и тогда число инверсий   есть четное число и равен  – 1, если перестановка   нечетная и тогда число инверсий   есть нечетное число.

Вопрос №10: (Определитель квадратной матрицы. Доказать свойство: определитель не изменяется при транспонировании матрицы.)

Определение определителя описывается в вопросе №6!

 Определитель не изменяется при транспонировании, это значит:

                    

 Доказательство:

 

   Замечание:

Следующие свойства определителей будут формулироваться только для строк. При этом из свойства 1 следует, что теми же свойствами будут обладать и столбцы.

Вопрос №11: (Определитель квадратной матрицы. Доказать свойство: определитель изменяет знак при перестановке двух его строк.)

Определение определителя описывается в вопросе №6!

При перестановке двух строк определителя он умножается на –1:

                   

 Доказательство:

Вопрос №12: (Определитель квадратной матрицы. Доказать свойство: при умножении строки на число определитель умножается на это число.)

Определение определителя описывается в вопросе №6!

При умножении элементов строки определителя на некоторое число весь определитель умножается на это число, это значит:

                            .

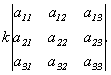 Доказательство:

  

Вопрос №13: (Определитель квадратной матрицы. Доказать свойство: определитель, одна из строк которого представлена в виде суммы двух строк, является суммой двух определителей.)

Определение определителя описывается в вопросе №6!

Если каждый элемент n-го столбца или n-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце или соответственно в n-й строке имеет первые из упомянутых слагаемых, а другой - вторые; элементы, стоящие на остальных местах, у вех трех определителей одни и те же.

Доказательство:

det

Определитель является линейной функцией строк матриц стоящих на любом месте. Полилинейная функция строк.