9. Основные виды проекций.

В системах геометрического моделирования часто используется параллельная проекция. Точки объекта проецируются на картинную плоскость с помощью пучка параллельных некоторому направлению V лучей.

Преобразование описаний объектов на плоскость наблюдения вдоль линий, параллельных вектору нормали к плоскости наблюдения N, называется ортогональной проекцией (ортографической). В результате получается параллельная проекция, в которой лини и проекции перпендикулярны плоскости наблюдения.

П ерспективное изображение широко применяется в художественном, архитектурном и техническом графическом моделировании для создания представления об удаленности объектов от наблюдателя.

Одним из видов перспективного проецирования, часто используемым в графике, является одноточечная перспективная проекция, задаваемая положением центра проекции - точки схода прямых, перпендикулярных картинной плоскости до преобразования. В часто реализуемом случае расположения наблюдателя в центре проекции, центр проекции называют точкой зрения. Преобразование центрального проецирования переводит пучок параллельных прямых в пучок с общей точкой пересечения. На рисунке точка M₁(x₁, y₁, z₁) переходит в M₂(x₂, y₂, z₂) по следующему закону:

,

, (2.1)

П оскольку практически все доступные устройства вывода графической информации являются плоскими, в машинной графике необходимо решать задачу получения проекции пространственного изображения на картинную плоскость. Пусть точка схода P₀(0, 0, z₀) расположена на оси OZ, а картинная плоскость z1=const перпендикулярна оптической оси (т. е. оптическая ось совпадает c OZ), тогда точка P(x, y, z) проецируется из мировой системы координат xyz в плоские координаты XY на картинной плоскости.

, (2.2)

Недостатком соотношений 2.1 и 2.2 является их нелинейность. Она может быть устранена введением однородных координат (X, Y, Z, W).

10. Ортографическая проекция. Основные свойства. Матрица переходов.

При ортографической проекции картинная плоскость совпадает с одной из координатных плоскостей или параллельна ей. Матрица проектирования вдоль оси Х на плоскость YZ имеет вид:

В случае, если плоскость проектирования параллельна координатной плоскости, необходимо умножить матрицу [P_x] на матрицу сдвига. В результате получаем

*Px =

При аксонометрической проекции проектирующие прямые перпендикулярны картинной плоскости.

В соответствии со взаимным расположением плоскости проектирования и координатных осей различают три вида проекций:

триметрию - нормальный вектор картинной плоскости образует с ортами координатных осей попарно различные углы;

диметрию - два угла между нормалью картинной плоскости и координатными осями равны;

изометрию - все три угла между нормалью картинной плоскости и координатными осями равны.

Каждый из трех видов указанных проекций получается комбинацией поворотов, за которой следует параллельное проектирование.

При аксонометрическом проецировании сохраняется параллельность прямых, а углы изменяются; измерение же расстояний вдоль каждой из координатных осей в общем случае должно выполняться со своим масштабным коэффициентом.

При изометрических проекциях укорачивания вдоль всех координатных осей одинаковы, поэтому можно производить измерения вдоль направлений осей с одним и тем же масштабом (отсюда и название изометрия).

При диметрической проекции две из трех осей сокращены одинаково, т.е. из трех углов между нормалью к плоскости проекции и главными координатными осями два угла одинаковы

13. Представление пространственных форм с помощью полигональных сеток. Достоинства и недостатки.

Полигональная сетка представляет собой поверхность многогранника, аппроксимирующего тело заданным способом. В зависимости от способа аппроксимации многогранник может находиться внутри аппроксимируемого тела, пересекать его или заключать в себе. В последнем случае, если многогранник выпуклый, полигональная сетка является выпуклой оболочкой тела. Грани многогранника, как правило, представляют собой выпуклые многоугольники, зачастую треугольники, что связано с удобством реализации для треугольников ряда алгоритмов (закраска, вычисление пересечений граней и т.д.). Построение аппроксимирующего многогранника с треугольными гранями называется триангуляцией. Способ построения полигональной сетки выбирается в соответствии с целью (расчет массово-инерционных характеристик однородного тела, вычисление площади поверхности тела, оценка принадлежности телу точки пространства, визуализация тела). Поскольку в нашем случае целью является изображение, вершины полигональной сетки удобно расположить на поверхности тела по некоторому закону. Очевидно, что при выбранном законе расположения вершин, точность аппроксимации данного тела будет определяться величиной разбиения.

Каркасное (проволочное, wire) изображение тела представляет собой совокупность линий, расположенных на поверхности тела или вблизи нее. Пример каркасного и фотореалистичного изображения одной и той же поверхности.

О чевидными серьезными недостатками каркасного изображения являются:

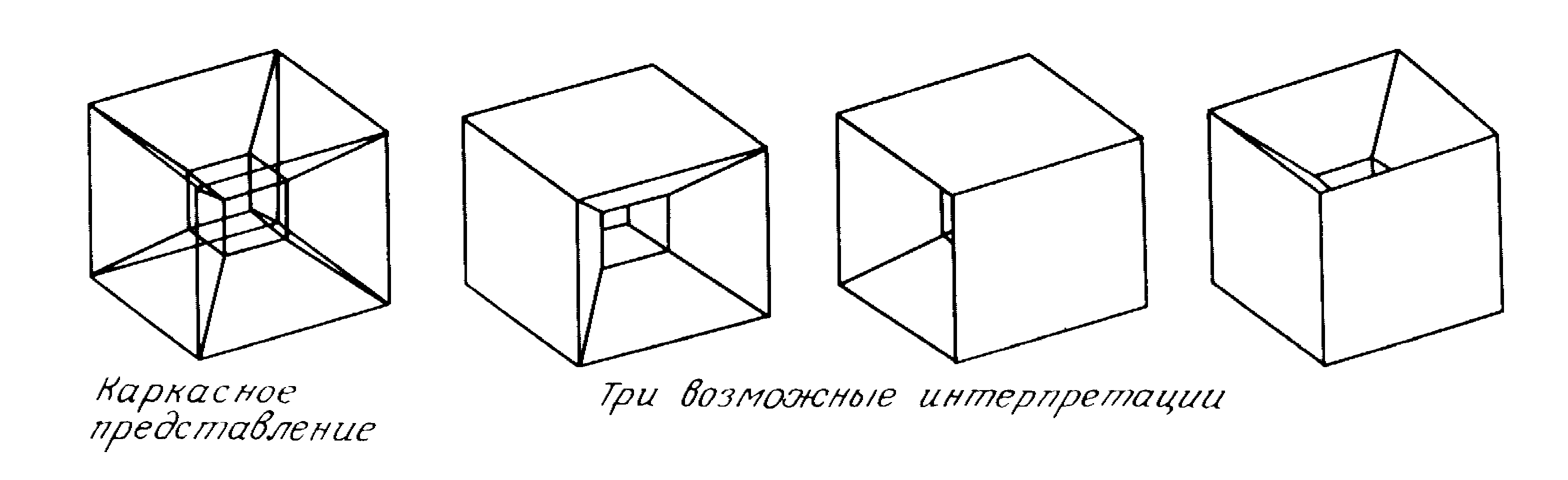- неоднозначность восприятия, обусловленная невозможностью отличить "скрытые" воображаемые грани от "видимых" и тем самым определить границы тела.

-невозможность правильного изображения криволинейных граней, так как видимый контур тела с криволинейными гранями в общем случае не совпадает с линиями каркасной модели Для более точного изображения видимого контура требуется высокая степень разбиения.

- высокая степень условности изображения из-за отсутствия видимой поверхности тела с ее цветом, фактурой и т.д.

К достоинствам каркасного изображения относятся сравнительная простота его реализации и невысокие требования к объему памяти и быстродействию ЭВМ. В графических программах режим каркасного изображения эффективно используется в тех случаях, когда не требуется детальная прорисовка модели, а иногда состоящий из параметрических линий каркас подчеркивает характерные особенности геометрии модели.