Вирази вільних складових загального розв’язку

Корені характеристичного рівняння	Вирази вільної складової
Корені  дійсні й різні
Корені  дійсні і рівні
Корені комплексно-спряжені

Необхідно пам’ятати, що, оскільки в лінійному колі з часом вільна складова згасає, дійсна складова − коренів характеристичного рівняння, не може бути позитивною.

При дійсних коренях вільна складова перехідної функції  монотонно згасає (при t→∞), і має місце аперіодичний перехідний процес. Наявність пари комплексно-спряжених корінь обумовлює появу загасаючих синусоїдальних коливань (коливальний перехідний процес).

Оскільки фізично коливальний процес пов'язаний з періодичним обміном енергією між магнітним полем котушки індуктивності й електричним полем конденсатора, комплексно-спряжені корені можуть мати місце тільки для кіл, що містять обидва типи накопичувачів.

Швидкість загасання коливань прийнято характеризувати відношенням

яке називається декрементом коливання, або натуральним логарифмом цього відношення

,

називаним логарифмічним декрементом коливання, де

Важливою характеристикою при дослідженні перехідних процесів є постійна часу τ, обумовлена для кіл першого порядку, як:

де р – корінь характеристичного рівняння.

Постійну часу можна інтерпретувати як часовий інтервал, протягом якого вільна складова зменшиться у порівнянні зі своїм початковим значенням в е разів. Теоретично перехідний процес триває нескінченно довго. Однак на практиці вважається, що він закінчується при .

Постійні інтегрування A₁, A₂ знаходять із початкових умов, які визначають за допомогою законів комутації.

Розрізняють незалежні й залежні (після комутаційні) початкові умови:

– незалежні початкові умови – значення струмів через індуктивності й значення напруг на ємностях, відомі з до комутаційного режиму роботи кола, які по законам комутації не змінюються стрибком

– залежні початкові умови – значення інших струмів і напруг при t = 0 у після комутаційній схемі, обумовлені незалежними початковими значеннями, які знаходяться із законів Кирхгофа для схеми після комутації.

1. Класичний метод розрахунку перехідних процесів у колах першого порядку

Задача 1

Дано: На вхід кола з опором R= 1000 Ом подається напруга U=25 B. Визначити індуктивність та струм у колі, якщо відомо, що в деякий момент струм приймає значення .

Рис.2

Розв’язання:

Запишемо рівняння електричної рівноваги для заданого кола за другим законом Кірхгофа:

Розв’язок цього рівняння представимо у вигляді:

.

До комутації струму в котушці не було, отже,

.

Стала складова струму після комутації

.

Вільну складову струму, знаходимо з розв’язання однорідного диференціального рівняння першого порядку, записаного для кола за першим законом Кірхгофа:

Це рівняння описує процесс в скомутованому колі без джерел енергії (вільний процес). Оскільки джерела енергії відсутні, то вільний процесс – згасаючий.

Складемо характеристичне рівняння. Пам’ятаємо, що характеристичне рівняння складається для пошуку вільної складової перехідного струму. Для отримання характеристичне рівняння будь-якого диференційного рівняння, в даному випадку рівняння кола без джерел енергії (вільний режим), необхідно в ньому замінити на .

.

Оскільки, p – реальний, то розв’язок знаходимо у вигляді:

З початкових умов визначимо постійну інтегрування А і вільну складову струму:

або

; ;

Закон змінення струму через індуктивність має вигляд:

_.

Визначимо сталу часу. Оскільки в момент часу струм приймає значення , підставимо значення у вираз для та визначимо сталу часу τ:

;

c.

Величину індуктивності знаходимо з характеристичного рівняння:

Гн.

Струму у колі змінюється за законом:

Задача 2

Дано: U=30 B R= 1 Ом R1=2 Ом L=2 Гн t1=2 c Визначити:

Рис. 3

Розв’язання:

Для визначення закону зміни струму через індуктивність необхідно провести аналіз перехідного процесу в колі (рис. 3) для двох випадків:

• ключ розімкнений ;

• ключ замкнений .

Диференційне рівняння для даного електричного кола (після першої комутації) за ІІ законом Кірхгофа має вигляд

Розв’язок цього рівняння знаходимо у вигляді: .

Проведемо розрахунок усталеного режиму до комутації (t=0-).

Проведемо розрахунок усталеного режиму після комутації (t→∞).

Визначимо вільні складові перехідних функцій. Вільний процес являє собою умовний процес, який протікає при відсутності джерел енергії за рахунок накопиченої до комутації енергії на реактивних елементах. Рівняння енергетичного балансу в колі, яке описує вільний процес (рис. 4, а), являє собою однорідне диференційне рівняння:

.

Існують два способи одержання характеристичного рівняння та визначення його коренів.

Перший спосіб полягає у виконання заміни на p у однорідному диференційному рівнянні. У нашому випадку, для використання заміни, рівняння необхідно іще раз про диференціювати:

Отже, корені будемо шукати як

та .

Другий спосіб називається методом “вхідного опору”. Для цього в після комутаційній схемі вилучаємо всі джерела енергії (вільний режим) та заміняємо jω на р (отримали операторну схему заміщення). Розриваємо коло у точках а­­–б (рис. 4, б) та записуємо вираз для вхідного опору відносно точок розриву.

а) б)

Рис. 4

Порівнюючи вирази характеристичного рівняння та його корені, отримані двома способами, приходимо до висновку, що вони ідентичні.

Отже, вільна складова струму

.

Визначимо постійну інтегрування А. Для цього знайдемо значення струму у момент комутації (t=0), застосувавши у даному випадку І закон комутації:

.

Запишемо вираз перехідного струму для першого випадку: .

Для момент комутації (t=0):

Перехідний струм через індуктивність:

.

2. t₁≤ t ≤ ∞

Після замикання ключа змінюється опір схеми. Диференційне рівняння для новоутвореного електричного кола (після другої комутації) за ІІ законом Кірхгофа має вигляд

Усталена складова перехідного струму до комутації (t=-0):

.

В момент другої комутації (t=t₁) через індуктивність протікає струм

Проведемо розрахунок усталеного режиму після комутації (t→∞).

Однорідне диференційне рівняння, для визначення вільної складової струму, має вигляд:

.

Електричне коло, якому відповідає дане рівняння зображене на рис. 5, а.

На рис. 5, б зображена операторна схема заміщення для одержання характеристичного рівняння та визначення його коренів p.

а) б) Рис. 5

Отже, вільна складова струму

Перехідний струм після другої комутації:

.

Визначимо постійну інтегрування А Для момент комутації (t=0):

Перехідний струм через індуктивність у випадку замикання ключа:

.

Рис. 6

Задача 3

Дано: U=24 B R1=100 Ом R2=200 Ом C=50 мкФ Визначити: –?

Рис. 7

Розв’язання:

До комутації (t=0-) коло було розімкнене, отже струм не протікав і ємність – розряджена:

Згідно з другим законом комутації: , отже у початковий момент часу (t=0) опір закорочений, і в колі протікає струм

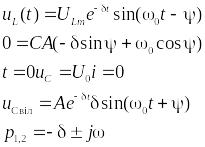
Пам’ятаємо, що перехідна функція складається з двох складових: вимушеної та вільної.

Вимушену складову знаходимо з розрахунку усталеного режиму після комутації.

Після комутації струм протікає до моменту повного заряду ємності, після чого ємність струму не пропускає і:

Складемо характеристичне рівняння скориставшись методом вхідного опору. Такому рівнянню відповідає вираз вхідного опору, для після комутаційної схеми без джерел енергії, прирівняний нулю:

Рис. 8.

Запишемо загальні вирази для перехідних величин та визначимо постійні інтегрування згідно нульових умов:

Отже, кінцевими виразами перехідних функції є:

Перевірку правильності проведення розрахунків здійснюємо за законами Кірхгофа.

Визначимо час t₁. Оскільки

.

52