
- •Курс лекций по дисциплине
- •Введение
- •4. Введение в математический анализ
- •4.1. Понятие функции и аргумента Математический анализ изучает переменные величины и функциональные зависимости между ними.
- •4.2 Пределы функции в точке и на бесконечности
- •4.3. Непрерывность функции и точки разрыва
- •4.4. Производная функции
- •4.5. Дифференцирование функций
- •Практическое занятие 2.
- •I Производная.
- •II. Производная сложной функции
- •3.Найти интервалы вогнутости и выпуклости, а также точки перегиба кривой Гаусса
- •4.Найти асимптоты кривых
- •4.Исследовать функцию с помощью производной и построить ее график
- •4.6. Производные высших порядков
- •4.7. Исследование функций с помощью производных
- •4.7.1. Основные теоремы дифференциального исчисления
- •4.7.2.Признак монотонности функций
- •4.7.3. Локальные экстремумы функций
- •4.7.4. Выпуклость, вогнутость графика функции и точки перегиба
- •4.7.5. Асимптоты графиков функций
- •4.7.6. Общая схема исследования функций и построения графиков
- •Решение:
4.2 Пределы функции в точке и на бесконечности
Введем понятие предела функции в точке и на бесконечности.
Пусть на множестве D задана функция у = f(х). Рассмотрим поведение функции при стремлении аргумента к числу х0, т.е. х→х0. Выберем произвольную последовательность значений аргумента {x1,x2,…xn,…}={xn}, общий член которой xn неограниченно близко приближается к числу х0, т.е. стремится xn→х0. При этом соответствующие значения функции образуют числовую последовательность {f(x1), f(x2),…f(xn),…} = {f(xn)}.
Д адим
определение предела функции в точке.
адим
определение предела функции в точке.
Определение: Число А называется пределом функции у = f(х) в точке х = х0, если для любой последовательности значений аргумента {xn}, стремящейся к х0, т.е. xn→х0, соответствующая последовательность значений функции {f(xn)} стремится к числу А, т.е. f(xn)→A.
Предел
в точке обозначается:
 .
.
Существуют также односторонние пределы в точке - пределы слева и справа, когда значения аргумента приближаются к точке х=х0 со стороны больших или меньших значений:


Теорема.
Для того чтобы функция имела у = f(х)
имела предел в точке х=х0 необходимо
и достаточно, чтобы в этой точке
существовали равные между собой правый
и левый пределы, которые и определяют
предел функции в точке:

Введём понятие предела функции на бесконечности. В этом случае значение аргумента неограниченно возрастает до бесконечности. Дадим Определение:
Определение: Число А называется пределом функции у = f(х) на бесконечности при х→∞, если для любой последовательности значений аргумента, стремящейся к бесконечности, т.е. xn→∞, соответствующая последовательность значений функции стремится к числу А, т.е. f(xn)→A.
Предел на
бесконечности обозначается:
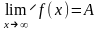 .
.
Отметим, что
функция может иметь пределы как на +∞,
так и на -∞:
 .
.
замечательные пределы и их следствия
Первый замечательный предел:
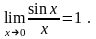 или
или
 ,
,
где u=u(x)→0 при x→0
Следствия из первого замечательного предела:
 ;
; ;
;
 .
.
Пример.
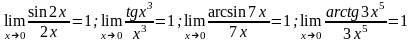 .
.
Второй
замечательный предел:
 или
или
 ,
где е 2.73…-натуральное
число, а logex
= lnx называется натуральным
логарифмом.
,
где е 2.73…-натуральное
число, а logex
= lnx называется натуральным
логарифмом.
Следствия из второго замечательного предела:
 ;
; ;
;
 ;
; .
.
бесконечно малые и бесконечно большие функции
Определение:
Функция
 называется бесконечно малой в точке
х=х0 или на бесконечности при х,
если её пределы равны нулю:
называется бесконечно малой в точке
х=х0 или на бесконечности при х,
если её пределы равны нулю: .
.
О пределение:
Функция
пределение:
Функция
 называется бесконечно большой в точке
х=х0 или на бесконечности при х,
если её пределы равны бесконечности:
называется бесконечно большой в точке
х=х0 или на бесконечности при х,
если её пределы равны бесконечности: .
.
Следует отметить,
что одна и та же функция может быть
одновременно бесконечно малой или
бесконечно большой в разных точках. На
рисунке функция является бесконечно
малой в точке х=1 и при
 ,
а в точке х=0 эта функция является
бесконечно большой.
,
а в точке х=0 эта функция является
бесконечно большой.
Теорема о связи
бесконечно малых или бесконечно больших
функций: Если функция
является бесконечно малой в точке х=х0
или на бесконечности при х,
то функция
 является бесконечно большой и наоборот,
если
- бесконечно большая функция, то
является бесконечно большой и наоборот,
если
- бесконечно большая функция, то
 является бесконечно малой функцией.
является бесконечно малой функцией.
Пример.
Функция
 является
б.малой в точке х=2, т.к.
является
б.малой в точке х=2, т.к. ,
а функция
,
а функция
 является б.большой в точке х=2, т.к.
является б.большой в точке х=2, т.к.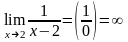 .
.
Определение:
Две бесконечно малые функции
 в точке х=х0 или на бесконечности
при х называются
эквивалентными, если предел их отношения
равен единице,
в точке х=х0 или на бесконечности
при х называются
эквивалентными, если предел их отношения
равен единице,
т.е.
 .
.
При нахождении пределов б.малые функции можно заменять на эквивалентные.
Составим таблицу эквивалентных бесконечно малых функций, основываясь на двух замечательных пределах и их следствиях.
таблица эквивалентных бесконечно малых функций
sinu~ u; tgu~ u; arcsinu~ u; arctgu~u,
еu-1~u; 3)au-1~u lna; 4)ln(1+u) ~u; 5)(u+1) ~ u; 6) (1-cosu)~
 ,
,
где u=u(x)→0 –б.малая функция;
Теорема об
арифметических операциях над пределами:
Если функции f(x)
и имеют конечные пределы в точке х=х0
или на бесконечности при х
, то
имеют конечные пределы в точке х=х0
или на бесконечности при х
, то
 ;
; ;
;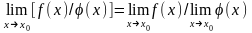 при условии
при условии
 .
.
вычисление пределов
При вычислении пределов необходимо выделить случаи когда функция определена или неопределена в предельной точке.
Если функция
определена в предельной точке х=х0,
то вычисление предела сводится к
вычислению частного значения функции
в этой точке путем подстановки в неё
значения аргумента, т.е.
 .
.
Пример.
 .
.
Если функция
неопределена в предельной точке х=х0,
то для характерных неопределенностей
типа: имеется ряд практических приемов
вычисления пределов для раскрытия этих
неопределенностей.
имеется ряд практических приемов
вычисления пределов для раскрытия этих
неопределенностей.
1. Неопределенность
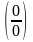 .
.
Если эта неопределенность возникла для тригонометрических функций, то можно использовать первый замечательный предел и его следствия, а также можно провести замену эквивалентных б.малых функций.
П ример.
ример.
 =
sin2 x=(sinx)2~x2;
arctg3x~3x;
(e6x-1)
~6x =
=
sin2 x=(sinx)2~x2;
arctg3x~3x;
(e6x-1)
~6x =
= .
.
Если эта неопределенность возникла при делении многочленов, то нужно в числителе и знаменателе выделить и сократить сомножитель, стремящийся к 0.
Пример.
 .
.
Неопределенность
 раскрывается путем деления числителя
и знаменателя дроби на наибольшую
степень переменной х и замены б.большой
переменной х→ на
новую б.малую переменную
раскрывается путем деления числителя
и знаменателя дроби на наибольшую
степень переменной х и замены б.большой
переменной х→ на
новую б.малую переменную
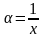 0.
0.
П ример.
ример.
 0
при х→ =
0
при х→ = .
.
Неопределенности
 путем
преобразования приводятся к
неопределенностям вида:
путем
преобразования приводятся к
неопределенностям вида: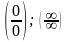 .
.
Примеры.
1) ;
;
2)
 .
.
Неопределенность
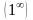 раскрывается с помощью второго
замечательного предела.
раскрывается с помощью второго
замечательного предела.
Пример.

 =
2x=u, х=1/2u;
х 0;u0
=
=
2x=u, х=1/2u;
х 0;u0
= =
=
= .
.
Практическое занятие 1
1. Вычислить предел функции натурального аргумента.
1.1. 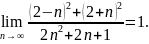
 1.2.
1.2.

 1.4.
1.4.

1.5. 

2. Вычислить предел функции натурального аргумента.
2.1. 
 2.3.
2.3. 

2.2. 
 2.4.
2.4. 

2.5. 

3. Вычислить предел функции натурального аргумента.
3.1. 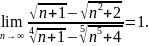
 3.2.
3.2. 

3.3. 
 3.4.
3.4. 

3.5. 

Домашняя работа
Вычислить указанные пределы (не пользуясь правилом Лапиталя).
1.1 1.4
1.4
1.2 1.5.
1.5. 

1.3 1.6
1.6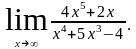
1.7 1.8.
1.8. 

1.9 1.10.
1.10. 

1.11 1.12.
1.12. 

1.13
2.Вычислить пределы функции
2.1.

 2.2
2.2
2.3 2.4
2.4
2.5.

 2.6
2.6
2.7 2.8
2.8
2.9 2.10
2.10
2.11.

 2.12
2.12
2.13 2.14.
2.14. 

2.15.

 2.16
2.16
