Эоп для тел простой формы Линейный вибратор

Отражающие свойства цели можно определить, рассматривая ее как антенну, являющуюся одновременно приемной и передающей. Такой подход удобен для линейных вибраторов. На рисунке показано расположение векторов Е_ц, Н_ц и П_ц относительно линейного вибратора.

(РИСУНОК)

Наведенная в таком вибраторе ЭДС е_ц=Е_цF_E(θ)h_, где F_E(θ) – диаграмма направленности вибратора по Е, h_ - действующая высота вибратора. Ток, возникающий в вибраторе под действием е_ц равен I_ц=е_ц/z_ц=Е_цF_E(θ)h_/z_ц (1). z_ц – входное сопротивление.

В формуле (1) ЭДС и ток можно рассматривать как приведенные к середине симметричного вибратора (точка пучности тока для полуволнового вибратора). В результате протекания тока вибратора I_ц возникает вторичное излучение. Напряженность поля вибратора в дальней зоне (у РЛС) Е_р=60πI_цh_F_E(θ)/(λ). Подставляя в эту формулу (1), получаем (2). Теперь с помощью соотношения σ_ц=4π²(Е_р/Е_ц)² находим ЭОП: 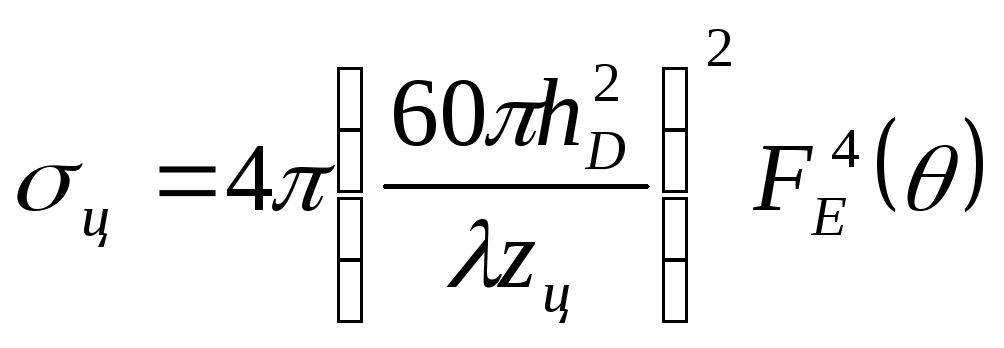(3). В элементарном вибраторе длинойl действующая высота h_=l – геометрическая длина. При определении входного сопротивления следует иметь в виду, что емкость между концами вибратора из-за малых размеров невелика. Это определяет характер реактивной составляющей входного сопротивления. Приближенно его можно определить следующим образом:

х_ц=½ρ_В∙ctg(2π/λ)≈ρ_Вλ/(πl),

где ρ_В – волновое сопротивление вибратора: ρ_В=120∙ln(l/r). Для очень тонкого вибратора ρ_В~1000 Ом.

Активная составляющая входного сопротивления в основном определяется сопротивлением излучения, которое для элементарного вибратора l<<λ: R_ц.изл=80π²(l/λ)²<<х_ц (4). . Диаграмма направленности элементарного вибратора может быть оценена так: f_E(θ)=cosθ (5). Подставляя (4) и (5) в соотношение (3) с учетом того, что h_=l, получаем для ЭОП цели: (6).(7). Т.о. отношение ЭОП к квадрату линейного размера пропорциональна величине (l/λ)⁴. Это характерно для тел любой формы, удовлетворяющих условию l<<λ. Для полуволнового вибратора h_=λ/π. Т.к. вибратор настроен в резонанс, то его входное сопротивление z_ц≈R_ц.изл=73,2 Ом. Для полуволнового вибратора F_E(θ)=cos(π/2∙sinθ)/cosθ (8). Для углов θ, близких к 0, можно принять F_E(θ)≈cosθ. После подстановки соответствующих значений в выражение (3) получим: (9). Равенство F_E(θ)=cosθ точно выполняется, если изменяется не наклон вибратора к фронту падающей волны, а если вибратор лежит в плоскости фронта и меняется угол расположения вектора Е_ц относительно вибратора, таким образом, изменяется угол поляризации. При θ=0 ЭОП σ_ц.max=0,85λ² (10).

Т.о., ЭОП резонансного полуволнового вибратора значительно превышает его геометрическую площадь. Это обстоятельство используется для создания искусственных дипольных отражателей, создающих помехи РЛС военного назначения. В этом случае вибратор может занимать равновероятное положение в пределах углов от 0 до 90 градусов.

Эоп идеального проводящего тела, размеры которого значительно больше λ

Поверхности реальных целей являются обычно металлическими и имеют размеры, значительно превышающие λ. Задача рассеяния э/м волн такими поверхностями является одной из классических задач электродинамики, хотя до сих пор не существует общего метода ее решения для тел произвольной формы. В настоящее время решено лишь небольшое кол-во идеализированных задач (академик В. А. Фок). Поле вторичного излучения можно определить на основании принципа Гюйгенса-Кирхгофа. По нему каждый элемент облучаемой поверхности следует рассматривать как источник элементарной сферической волны с определенной амплитудой и фазой. Результирующее поле является их суперпозицией. В направлении на РЛС налагающиеся колебания имеют всевозможные сдвиги фаз, поэтому могут как усиливать, так и ослаблять друг друга – отражение носит резко интерференционный характер. Однако, для конкретного применения данного принципа требуется знание распределения тока на проводящей поверхности, возбуждаемого первичной волной. Точное решение этой задачи найдено лишь в некоторых частных случаях. Обычно задается приближенное распределение тока. Для случая, когда радиус кривизны любого элемента поверхности много больше λ, вся поверхность делится на освещенную, т.е. обращенную к источнику (РЛС) и область тени. Для упрощения расчетов пренебрегают наличием областей полутени и считают, что в области тени ток равен 0. Целесообразно при определении тока в каждой точке заменять криволинейные участки поверхности соответствующим участком касательной поверхности. Расстояние  между РЛС и целью считается достаточно большим по сравнению с размерами цели и λ. Поэтому передающую волну (первичную) можно полагать плоской. Для выполнения граничных условий требуется, чтобы нормальная составляющая магнитного поля и тангенциальная составляющая вектора Е были равны 0. Что касается тангенциальных составляющих вектора Н, то они суммируются. Формула показывает, что ЭОП зависит от формы и размеров отражающего волну тела и зависит от длины волны:

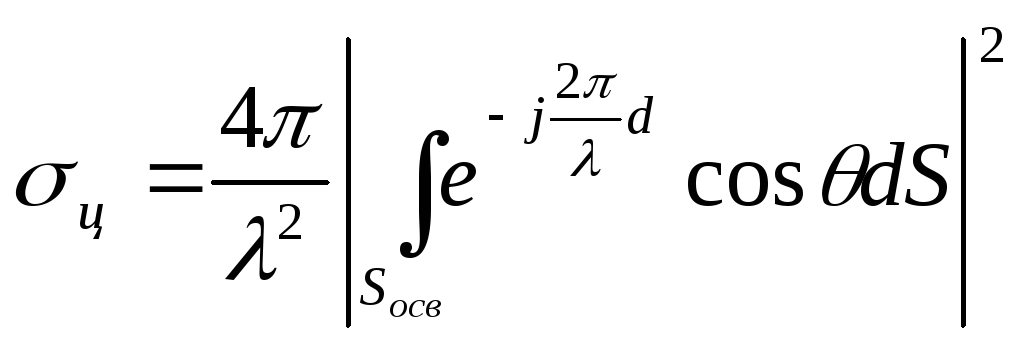, где j – плотность тока.