
Лабораторные работы / отчет по ТПР № 3
.docУфимский Государственный Авиационный Технический Университет
Кафедра автоматизированных технологических систем
Отчет к лабораторной работе № 3
«Методы многомерной оптимизации»
Выполнили:
Проверил:
Уфа-2006
ЦЕЛЬ РАБОТЫ
Целью работы является изучение методов многомерной оптимизации функции нескольких переменных и получение практических навыков по разработке алгоритмов реализации изучаемых методов.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Многомерная оптимизация заключается в поиске экстремумов функции нескольких переменных F = F(x1 х2, ..., хn). Из всего многообразия разработанных к настоящему времени методов рассмотрим два относительно простых метода поиска точки X*= {х1*, х2*, ..., хn*}T, доставляющей минимум функции F* = F(x1*, х2*, ..., хn*).
2.1. Метод координатного спуска
Метод координатного спуска заключается в том, что в качестве направлений траектории спуска от предыдущей точки поиска Х(k-1) к последующей Х(k) принимают поочередно направления координатных осей xi (i = 1, 2, ..., п). После спуска на один шаг по координате x1 переходим к спуску на один шаг по координате х2, а затем двигаемся вдоль координаты х3 и т.д., пока не перейдем в следующую точку поиска Х(1) с координатами Х1(1),X 2(1) , ... X.п(1)
Движение по траектории спуска от предыдущей точки Х(k-1) к последующей Х(k) следует продолжать до тех пор, пока не будут достигнуты окрестности точки минимума X*, определяемые точностью вычислений.
Для поиска координат точки Х(k) на каждом шаге итерации можно использовать любой из методов одномерной минимизации: метод золотого сечения, метод деления отрезка пополам, метод интерполяции-экстраполяции и др.
Ниже рассмотрен один из этих методов - метод поразрядного приближения.
Метод поразрядного приближения является разновидностью метода равномерного поиска и не требует перебора всех точек функции F(x) в направлении выбранной координаты хi Алгоритм этого метода и состоит в следующем.
Задаем начальную точку поиска Х(0) (приблизительно слева от искомой точки минимума X*) с координатами х1(0), х2(0) ... хп(0) и выбираем первое направление спуска, например, X1.
В точке х1(0) вычисляем значение оптимизируемой функции F(1) при условии неизменности остальных координатхj(0) (j = 2, ..., п).
Далее полагаем G = F(1) и задаем новую точку расчета X1 в направлении увеличения координаты x1 на шаг h (x1 = x1 + h), в которой затем вычисляем функцию F(1). После чего проверяем условие убывания функции в новой точке: F(1) < G.
Если это условие выполняется, то полагаем G = F(k) и вновь увеличим на шаг h координату x1, в которой далее вычисляем функцию F(1).
Если же проверяемое условие F(1) < G не выполняется, то полагаем G = F(1), уменьшаем шаг h, например, в четыре раза, и меняем направление движения вдоль координаты х1 на противоположное, т.е. принимаем h = -h/4. Далее проверяем условие достижения заданной точности \h\< ε вычисления координаты х1(1) на этом шаге итерации.
Если это условие точности достигнуто, то переходим к следующей координате х2, повторяем изложенный выше цикл вычислений для новой
координаты, но уже при найденном значении x1(1), до определения х2(1). Затем
переходим к координате х3, вычисляем х3(1) при найденных ранее значениях
х1(1) и х1(2), переходим к следующей координате и т.д., пока не будет полностью осуществлен переход в следующую точку итерации Х(1) по всем координатамх xi (i= 1,2, ..., п).
Если же условие точности вычисления координаты х1(1) не выполняется, то продолжим вычисления по изложенному выше циклу, пока точность вычислений по координате x1 на рассматриваемом шаге итерации не будет достигнута.
Важным условием вычислений для рассматриваемого метода координатного спуска является использование для каждых последующих вычислений найденных ранее значений координат Xi даже внутри одной итерации.
Процедуру спуска можно прекратить при выполнении условия | Х(k) —. X(k-i)| E где E _ погрешность вычислений. При этом решением задачи следует считать X* = Х(k).
2.2. Метод спирального координатного спуска
Метод спирального координатного спуска отличается от рассмотренного выше лишь тем, что шаг h меняется каждый раз при переходе от поиска минимума по одной переменной к поиску минимума по другой переменной. В трехмерном пространстве это напоминает спуск во впадину по спирали. Обычно этот метод дает некоторое сокращение времени поиска.
ПРАКТИЧЕСКАЯ ЧАСТЬ
задание на работу:
Найти методом координатного спуска X, *минимизировать квадратичную функцию F с точностью 0,01:
F(x1.x2) = х14 + 2x24 – x12x22 + 2x1 + х2
Составим блок-схемы алгоритма расчетов:
Алгоритм многомерной оптимизации

Алгоритм одномерной минимизации (поразрядного приближения) для координаты х
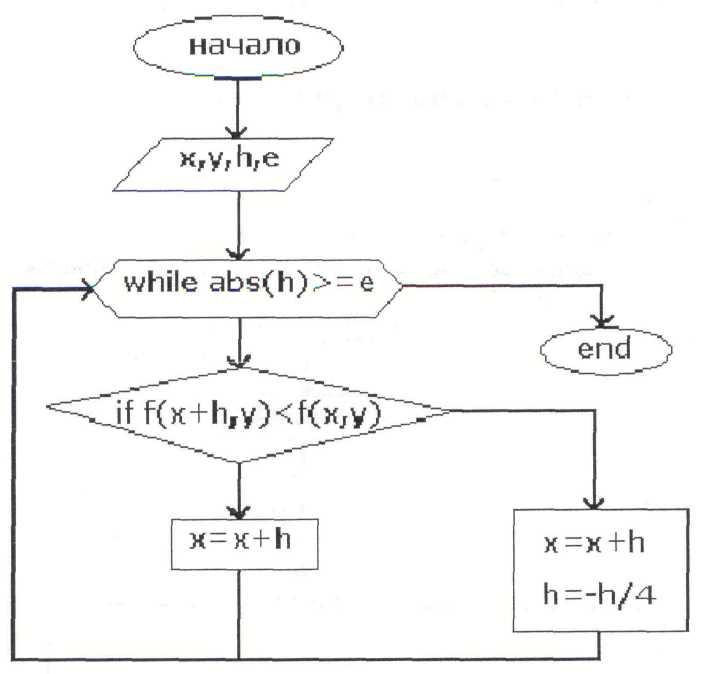
для координаты у

Напишем и отладим программу:
function[x0,y0,z0]=osnovnaia(x,y, e, h)
hold on
[X,Y]=meshgrid(-5:0.2:5, -5:0.2:5);
Z=fan(X);
mesh(XJ,Z)
l=inf;
while l>e;
x1 =x;
y1=y;
x=minx(x,y, e, h);
y=miny(x,y,e,h);
l=sqrt(((x-x1)^2) + (y-y1)^2);
end
x0=x;
y0=y;
z=0fan(x0,y0);
plot3(xO,yO,zO;’*’);
function x=minx(x,y, e, h)
while abs(h)>e
if fan(x+h,y) <fan(x,y)
x=x+h;
else
x=x+h;
h=-h/4;
end
end plot3(x,y,fan(x,y), '*r');
function y=miny(x,y, e, h)
while abs(h)>e
if fan (x,y+h) <fan (x, y)
y=y+h;
else
y=y+h;
h=-h/4;
end
end pbt3(x,y,fan(x,y), '*k');
function z=fan(x,y)
z=x. ^4+2*y.^4-(x.^2). *(y.^2)+2*x+y;
После отладки и запуска программы, мы получим
osnovnaia(-5,5,0.01,0.2)
ans = -0.8625
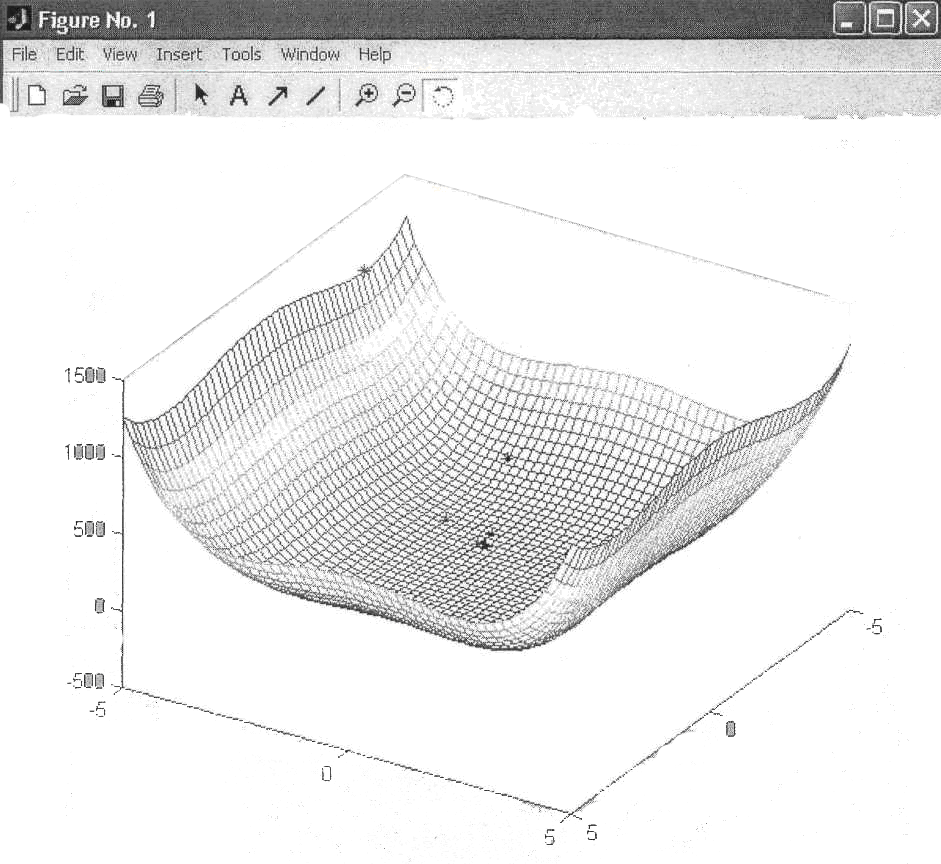
ВЫВОД: В ходе проделанной лабораторной работы, мы изучили методы многомерной оптимизации функции нескольких переменных и получили практические навыки по разработке алгоритмов реализации изучаемых методов.
Методом координатного спуска минимизировали квадратичную функцию F(x1x2) = х14+ 2х24 – X12x22 + 2х1 + х2 с точностью 0.01 и построили её график.
