Министерство образования рф Костромской государственный технологический университет
Кафедра высшей математики
Краткий справочник
по математике для специальностей инженерно-технического профиля
Кострома
2002 г
Глава I. Элементы линейной алгебры. 3
§1.1. Определители. 3
§1.2. Матрицы и линейные операции над ними. 3
Глава II. Векторная алгебра. 4
§2.1 Основные понятия. 4
§2.2. Операции над векторами. 4
§ 2.3. Переход к новому базису. 4
ГЛАВА III. КОМПЛЕКСНЫЕ ЧИСЛА. 4
§ 3.1. Представление комплексных чисел. 4
§ 3.2. Действия над комплексными числами 5
ГЛАВА IV. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ. 5
ГЛАВА V. ОПЕРАЦИИ МАТЕМАТИЧЕСКОЙ ЛОГИКИ. 6
ГЛАВА VI. КОМБИНАТОРИКА. 6
ГЛАВА VII. ЭЛЕМЕНТАРНАЯ АЛГЕБРА. 6
§ 7.1. Преобразования графиков функций. 6
§ 7.2. Корень уравнения. 7
ГЛАВА VIII. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ. 7
ГЛАВА IX. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ И НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. 7
ГЛАВА X. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ. 8
§ 10.1. Неопределенный интеграл. 8
§ 10.2. Определенный интеграл. 9
§ 10.3. Двойной интеграл. 9
ГЛАВА XI. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ. 10
ГЛАВА XII. ЧИСЛОВЫЕ И ФУНКЦИОНАЛЬНЫЕ РЯДЫ. 10
§ 12.1. Числовые ряды. 10
§ 12.2. Функциональные ряды. 11
ГЛАВА XIII. Аналитическая геометрия. 11
§ 13.1. Аналитическая геометрия на плоскости. 11
§ 13.2. Аналитическая геометрия в пространстве. 12
ГЛАВА XIV. ТЕОРИЯ ВЕРОЯТНОСТЕЙ. 12
§ 14.1. Случайные события. 12
§ 14.2. Случайные величины. 12
ГЛАВА XV. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА. 13
Глава I. Элементы линейной алгебры. §1.1. Определители.
Определение: Матрицей называется
таблица чисел, в которой m
строк и n столбцов
,
где
– элементы матрицы,
– номер строки,
– номер столбца
Только для квадратных матриц
введено понятие определителя.
Теорема: Определитель матрицы
или определитель n-го
порядка – это число, равное сумме
произведений элементов какого-либо
столбца (строки) на их алгебраические
дополнения. Например для второй строки:
,
где
– алгебраическое дополнение к элементу
;
Определение: Минором
элемента
называется определитель, получаемый
из данного после вычеркивания i-ой
строки и j-го
столбца.
В частных случаях:
или схематический (метод треугольников):
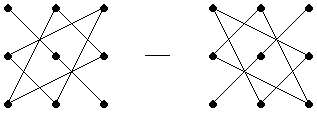
§1.2. Матрицы и линейные операции над ними.
,
,
,
справедливо:
Глава II. Векторная алгебра.
§2.1 Основные понятия.
Если
,
где
;
;
– координаты вектора
,
,
,
– вектора базиса; то модуль или
длина вектора
определяется по формуле:
Если вектора
и
коллинеарны, то
§2.2. Операции над векторами.
Пусть
,
.
Тогда
Скалярное произведение векторов и
:
В пространстве
последняя формула примет вид:
,
где
,
.
§ 2.3. Переход к новому базису.
В некотором базисе даны вектора:
,
,
.
Требуется найти координаты вектора
в новом базисе, образованном векторами
и
,
т.е. решить векторное уравнение:
,
,
которое сводится к системе линейных уравнений:
ГЛАВА III. КОМПЛЕКСНЫЕ ЧИСЛА.
§ 3.1. Представление комплексных чисел.