Задание 3.

По заданным координатам вершин треугольной пирамиды АВСD найти:

а) уравнения всех ребер пирамиды;

б) уравнения всех граней пирамиды;

в) длину высоты, опущенную из вершины D на грань ABC пирамиды.

Решение: а) Зная координаты всех вершин пирамиды, запишем уравнения ребер пирамиды, как прямых проходящих через две данные точки: (AB): (BС): (AC): (DA): (DB): (DC): б) Зная координаты всех вершин пирамиды, запишем уравнения граней пирамиды, как плоскостей проходящих через три данные точки: Запишем уравнение грани ABC, как уравнение плоскости , проходящей через три точки А(1;9;-1), В(5;-3;-1), C(8;3;4) и по следующей формуле: (АВС): . Запишем уравнение грани ADB, как уравнение плоскости , проходящей через три точки А(1;9;-1), В(5;-3;-1), D(4;-3;4) и по следующей формуле: (АDB): . Запишем уравнение грани ADC, как уравнение плоскости , проходящей через три точки А(1;9;-1), D(4;-3;4), C(8;3;4) и по следующей формуле: (АDC): . Запишем уравнение грани BDC, как уравнение плоскости , проходящей через три точки В(5;-3;-1), D(4;-3;4), C(8;3;4) и по следующей формуле: (BDС): . в) Определим длину высоты, опущенной из вершины D на грань ABC, как расстояние от точки D до плоскости АВС пирамиды. Вычислим данное расстояние по формуле: Ответ: (AB): (BС): (AC): (DA): (DB): (DC): б) ; ; ; . в)

Задание 4.

Вычислить пределы

а) ; б) ; в)

Решение:

а) Данный предел имеет неопределенность вида . Избавимся от неопределенности. Для этого, раскроем скобки в числителе и знаменателе дроби и приведем подобные. В результате получим следующий предел:

.

б) Данный предел имеет неопределенность вида . Сведем предел к неопределенности , которая снимается с помощью второго замечательного предела

в) Данный предел имеет неопределенность вида и критический множитель (x+1). Избавимся от неопределенности. Для этого, разложим числитель и знаменатель дроби на множители и сократим критические множители, т.е.

.

Задание 5.

Провести полное исследование функции и построить ее график.

Решение:

1. Функция определена на всей числовой оси за исключением точки где знаменатель дроби обращается в нуль, т.е. .

2. Так как область определения не симметрична относительно начала координат, то не имеет смысла говорить о четности (нечетности) функции. Функция общего вида т.к. и .

3. Легко определить точки, где функция пересекает координатные оси: при - точка пересечения с Оy , а при y=0 функция не имеет корней, т.к. . Видим, что числитель всегда положителен, а знаменатель не может равняться нулю. Следовательно точек пересечения с осью Ох нет.

4. Точка является точкой разрыва функции.

Найдем вертикальные асимптоты. Для этого будем искать пределы справа и слева при

Так как функция в точке имеет бесконечный разрыв, то прямая является для графика вертикальной асимптотой.

Найдем горизонтальные асимптоты. Для этого будем искать пределы:

горизонтальных асимптот нет.

Найдем наклонные асимптоты. Будем искать наклонную асимптоту в виде :

Теперь найдем

Наклонная асимптота графика функции y=x-1.

5. Найдем первую производную функции y:

Найдем критические точки, то есть приравняем Получим и

Определим знаки первой производной при переходе через критические точки используя метод интервалов:

0 2

При переходе через точку производная меняет знак с минуса на плюс, значит является точкой локального минимума, причем При переходе через точку производная меняет знак с плюса на минус, значит является точкой локального максимума, причем

Найдем интервалы монотонности функции. Функция возрастает на интервале , так как на этом интервале производная и убывает на (0,2) , так как на этом интервале производная

6. Вычислим вторую производную 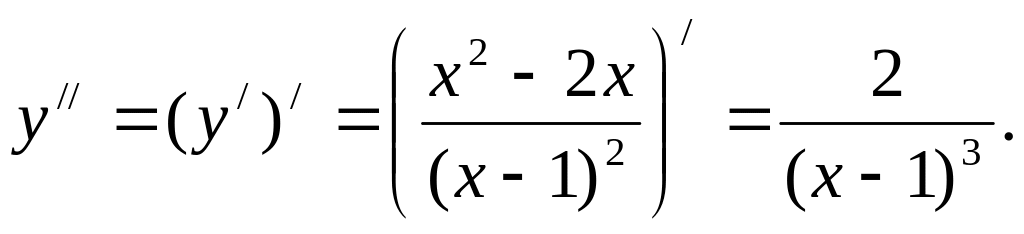Вторая производная в нуль не обращается, следовательно точек перегиба график функции не имеет. Но есть одна критическая точка 2-го рода, в которой вторая производная не определена: x₃=1. Исследовав знаки второй производной при переходе через данную критическую точку 2-го рода с помощью метода интервалов, получаем что на интервале вторая производная отрицательна, следовательно, функция на этом интервале будет вогнутой, а в интервале вторая производная положительная, значит, функция на этом интервале будет выпуклой.

7. Построим эскиз графика функции.
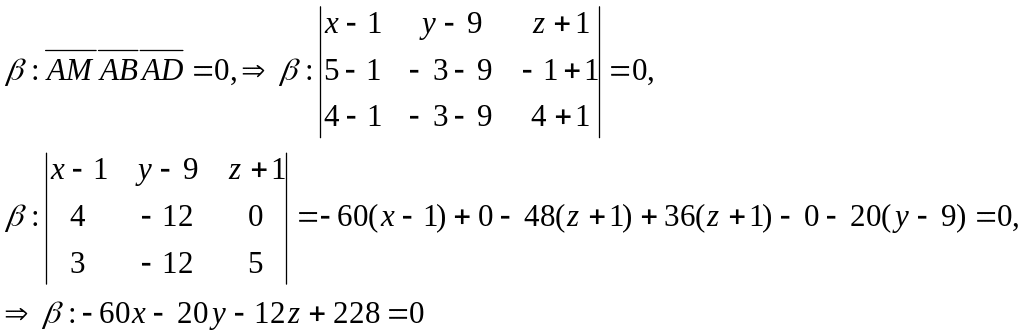