7.3.2.Поиск в ширину
При поиске в ширину порядок исследования дуг графа отличается. Поиск в ширину производится следующим образом:
Начинаем поиск с произвольной вершины r. Формируем множество текущих вершин A, включив в него вершину r.
Идем в ранее не пройденные вершины по всем дугам, имеющим начальную вершину, принадлежащую множеству A. Запоминаем эти дуги. Формируем множество A, включив в него конечные вершины пройденных дуг.
Процесс поиска (пункт 2) заканчивается, когда множество A станет пустым.
Поиск в ширину проиллюстрирован на рис. 7.17.
Для организации хранения множества A удобно использовать очередь. Алгоритм поиска в ширину представлен укрупненной блок-схемой на рис.7.18.
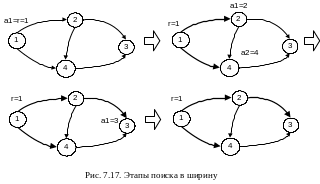
В алгоритме поиска в ширину используются те же структуры данных, что и в алгоритме поиска в глубину, за исключением того, что стек заменен очередью.
Реализация очереди может быть любой: на циклическом массиве, с помощью указателей или курсоров. Поскольку максимальная глубина очереди не может превышать числа вершин графа, то наиболее рационально реализовать очередь на циклическом массиве.
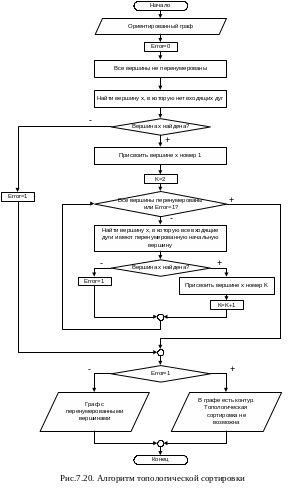
7.4.Топологическая сортировка графа
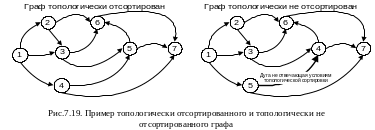
Если в ориентированном графе нет контуров (путей у которых начальная и конечная вершины совпадают), то можно перенумеровать вершины данного графа таким образом, что для каждой дуги (i,j) будет выполняться условие i<j. Такая перенумерация верши называется топологической сортировкой графа.
На рис.7.19 приведен топологически отсортированный и не отсортированный граф.
Алгоритм топологической сортировки может быть следующим:
Присвоить номер 1 вершине графа, в которую нет входящих дуг.
Присвоить следующий номер любой неперенумерованной вершине, для которой все предшествующие вершины перенумерованы. Здесь под предшествующими вершинами некоторой вершины u понимаются все вершины v, такие, что дуга (v,u) принадлежит множеству дуг графа. Если на данном шаге нет неперенумерованных вершины, для которой все предшествующие вершины перенумерованы, то это говорит о том, что исходный граф содержит контур (граф не может быть топологически отсортирован) и требуется остановить процесс перенумерации вершин.
Шаг 2 повторяется до тех пор, пока все вершины не будут перенумерованы.
Алгоритм топологической сортировки графа представлен укрупненной блок-схемой на рис.7.20. Программная реализация этого алгоритма представлена в листинге 7.11. В данном листинге граф задан матрицей смежности, элементы которой имеют логический тип. Далее (см. разд.7.5.1) возникнет необходимость осуществлять топологическую сортировку графа заданного матрицей весов, элементы которой имеют целочисленный тип. В связи с этим в листинге 7.11 проверка принадлежности дуги (i,j) графу оформлена в виде отдельной функции EDuga. Это позволит свести к минимуму изменения при переходе к хранению графа с помощью матрицы весов. Данные изменения затронут только функцию EDuga.
Топологическую сортировку графа можно выполнить и другим способом:
Присвоить переменной k значение n, где n - число вершин графа.
Найти вершину u, из которой нет выходящих дуг и присвоить ей номер k. Если на данном шаге нет вершины, из которой нет выходящих дуг, то это говорит о том, что исходный граф содержит контур и требуется остановить процесс перенумерации вершин.
Удалить вершину u вместе с входящими в нее дугами. Уменьшить k на единицу.
Шаги 2 и 3 повторять до тех пор, пока все вершины не будут перенумерованы.
