3. Определение динамических параметров настройки регулятора по динамическим параметрам объекта

Эффективность работы систем автоматического регулирования в. конечном итоге определяется качеством переходного процесса в системе, которое зависит от принятого критерия оценки качества параметров переходного процесса.

После выбора критерия оценки качества требуемого переходного процесса необходимо определить для конкретных значений динамических параметров ОУ значения параметров динамической настройки выбранного закона регулирования.

Инерционные свойства _З и Т_О управляемого технологического объекта препятствуют идеальной реализации поставленной задачи. В реальных производственных условиях перед каждым инженером возникает задача оптимизации контура управления, которая заключается в том, что для каждого объекта с известными динамическими параметрами _З, Т_О, К_ОБ необходимо определить значения параметров динамической настройки К_Р, Т_ИЗ, Т_П регулятора, при которых максимально возможно компенсируется влияние инерционных свойств объекта.

Для практических инженерных целей широкое распространение получили различные приближенные методы определения динамических параметров настройки. Эти методы не требуют графических построений, использования номограмм и построения траекторий переходных процессов.

В зависимости от технологических требований к характеру действующих на объект возмущений наилучшим, как рекомендует традиционный метод, может быть признан один из трех типовых процессов регулирования (см. рис.13).

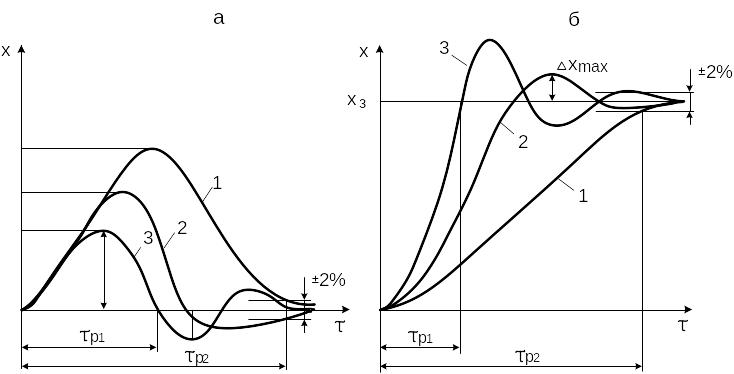
Рис.13 Типовые переходные процессы в системах автоматического регулирования: а) при отработке внутреннего возмущения (возмущение по нагрузке); б) при скачкообразном изменении задания.

1 – апериодический процесс с минимальным временем регулирования _Р  min;

2 – 20% перерегулирование (минимальное время максимального отклонения регулируемой величины от задания);

3 – минимальное значение квадратичного критерия

.

При инженерных методах выбора закона регулирования и близких к оптимальным значений параметров динамической настройки регулятора, рекомендуется пользоваться формулами [1], представленными в таблице 5.

В последнее время появились новые методы определения оптимальных значений параметров динамической настройки.

С целью выбора наилучшего метода в лаборатории кафедры ПКиСУ МГТУ был произведен сравнительный анализ количественных показателей качества переходных процессов. Сравнивались следующие методы:

1 – метод 20% перерегулирования с минимальным временем первого полупериода;

Таблица 5

Расчетные формулы для определения настроек регулятора для инерционного объекта с запаздыванием

Закон регулирования	Вид типового переходного процесса
	апериодический	20% перерегулирование	Минимум J’
Объекты с самовыравниванием (статические)
И
П
ПИ
ПИД
Объекты без самовыравнивания с интегральной составляющей
И	Не используют в связи с неустойчивостью переходного процесса
П			––
ПИ
ПИД

2 – метод минимального значения квадратичного критерия

; (26)

3 – метод оптимума по модулю (ОМ) передаточной функции или метод полной компенсации, минимизирующий величину обобщенного критерия [2,3]:

, (27)

где ₁ – весовой коэффициент; – сигнал рассогласования и его первая производная.

4 – метод максимальной степени устойчивости, минимизирующий величину перерегулирования на основании критерия максимальной устойчивости (близкий к апериодическому процессу регулирования) [4];

5 – метод минимизации весового интеграла ошибки, где весовой коэффициент есть экспоненциально возрастающая функция [5]:

(28)

На ЭВМ были проведены расчеты траекторий переходных процессов при оптимальных значениях параметров динамической настройки ПИ-закона. Настройки определили исходя из рекомендаций каждого рассмотренного метода для одного и того же инерционного объекта с запаздыванием с передаточной функцией вида:

(29)

Для упрощения расчета передаточная функция звена чистого запаздывания представлена в виде двучленного разложения в ряд Тейлора:

(30)

Оптимальные значения параметров контура регулирования определяются по различным методам. Траектории расчетных переходных процессов представлены на рис.14. По оси абсцисс время берется в относительных единицах /_З, где  - текущее время от начала возмущения по заданию.

Оценка качества переходных процессов в системе производилась по следующим показателям (более подробно в л.р. №4):

- время достижения заданного значения _Р1;

- общее время регулирования _Р2 – время, за которое регулируемая величина достигает заданной с ошибкой 2%;

- максимальная величина перерегулирования

Для удобства анализа полученные результаты сведены в таблицу 6.

Таблица 6

Показатели качества переходных процессов при оптимальных значениях параметров настройки ПИ-регулятора

N	Название метода	Значения настроек		Показатели качества
		КР	ТИ	Р1	Р2	, %
1	20% перерегулирование	10	20	2.56З	9.5З	16.20
2	Минимум	7	14	3.50З	9.5З	15.10
3	Оптимум по модулю	5	20	4.75З	10З	4.27
4	Максимальная степень устойчивости	3.7	18.8	6.50З	>20З	2.47
5	Минимум весового коэффициента ошибки	9.6	6.6	2.06З	9.5З	36.40

На основании анализа полученных данных можно сделать вывод: наиболее простым и достаточно точным методом определения оптимальных значений параметров динамической настройки регуляторов для инерционных объектов с запаздыванием является метод полной компенсации или метод оптимума по модулю (рис.14, траектория 3).

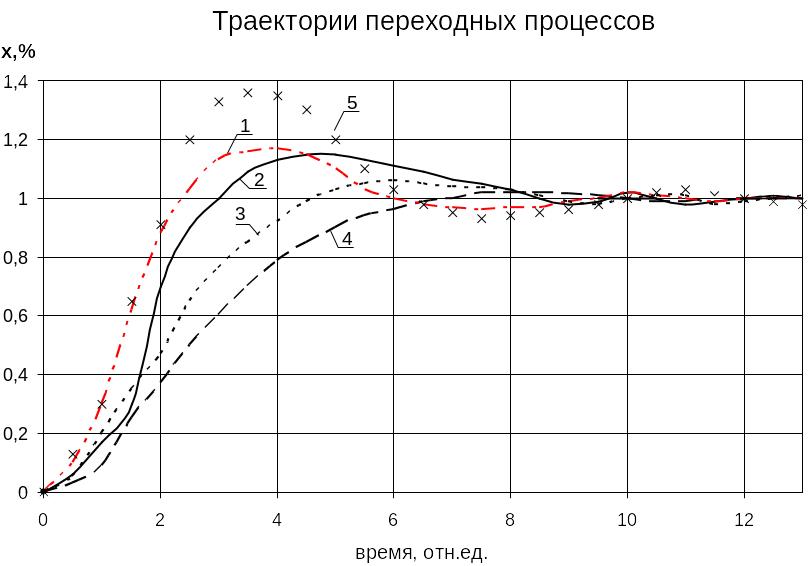
Рис.14 Траектории переходных процессов при оптимальных настройках контура управления, рассчитанных различными методами (нумерация совпадает с указанной в таблице 6)

Сущность метода ОМ передаточной функции в том, чтобы модуль передаточной функции замкнутой системы W_З(р) в как можно большей полосе частот (от  = 0 до ) был максимально приближен к единице. Оптимизация состоит в "пригонке" модуля W_З(р) к единице для возможно большей полосы частот.

Метод ОМ обеспечивает определение оптимальных значений динамических параметров настройки в соответствии с условиями:

(31)

где Т₁ – большая постоянная времени; Т₂ – меньшая (но соизмеримая с Т₁) постоянная времени. Объект аппроксимирован двумя инерционными звеньями с запаздыванием _З.

Применение данного метода не требует дополнительного исследования контура управления на устойчивость и обеспечивает получение стандартного переходного процесса

с количественными оценками качества переходного процесса