3. В отчете необходимо представить следующие материалы

3.1 Назначение статической характеристики, виды характеристик.

3.2 Общие сведения о методе наименьших разностей.

3.3 Таблица рабочего журнала наблюдений.

3.4 Результаты определения линии регрессии: таблица коэффициентов системы уравнений для определения линии регрессии, система уравнений, коэффициенты уравнения линии регрессии.

3.5 Уравнение коэффициента передачи ОУ.

3.6 График статической характеристики ОУ и линии регрессии.

3.7 График функции К_ОБ, полученный экспериментальным и расчетным путем.

3.8 Выводы по работе.

4. Вопросы для самоконтроля

4.1 Статическая характеристика ОУ. Виды статических характеристик.

4.2 Определение линии регрессии.

4.3 Суть метода наименьших квадратов.

4.4 Коэффициент передачи объекта. Метод определения.

Лабораторная работа №2 Экспериментальное определение кривой разгона и оценка динамических свойств объекта управления

Цель работы: экспериментальное исследование кривой разгона объекта и определение динамических параметров объекта, построение кривой разгона методом Эйлера

1. Общие сведения о динамических характеристиках

Состояние и поведение управления в неустановившихся переходных режимах определяются их динамическими свойствами. Динамические свойства ОУ могут быть определены линейными дифференциальными уравнениями, выражающими функциональную связь между входными и выходными величинами во времени.

Исходными данными для составления дифференциальных уравнений являются математические выражения физических законов, определяющих неустановившийся процесс в ОУ или другом элементе системы.

Определение динамических характеристик объектов с помощью дифференциальных уравнений может быть выполнено только для сравнительно простых объектов.

В общем виде зависимость выходной величины от входной в неустановившемся режиме выражается линейным дифференциальным уравнением вида:

(10)

где a₀ .. a_n, b₀ .. b_m – постоянные коэффициенты; n, n-1,.. и m, m‑1,..,1 – порядок производных.

В теории автоматического управления для записи и решения дифференциальных уравнений используется операторный метод, который при нулевых начальных условиях позволяет значительно упростить запись и решение дифференциальных уравнений. Уравнение (10) в операторной форме будет иметь вид:

(11)

где Y_ВЫХ(p), X_ВХ(p) – изображение по Лапласу выходного и входного параметров.

Операторная форма записи уравнения (11) позволяет получить очень важную динамическую характеристику ОУ – передаточную функцию W(p). Выражение, стоящее в скобках перед Y_ВЫХ(p), называется собственным оператором. Выражение, стоящее в скобках перед X_ВХ(p), называется оператором воздействия.

Передаточной функцией объекта называется отношение оператора воздействия к собственному оператору:

(12)

Передаточная функция объекта W(p) является записью дифференциального уравнения (10) в операторной форме и широко используется как основная динамическая характеристика объекта или другого элемента системы.

Наглядное представление о характере переходного процесса в объекте дает кривая разгона, которая представляет собой траекторию изменения выходного параметра во времени при однократном скачкообразном возмущении на входе.

По виду кривых разгона практически все объекты управления можно разделить на три вида:

- объекты с самовыравниванием (рис.8,а);

- объекты без самовыравнивания (рис.8,б);

- объекты с запаздыванием с самовыравниванием и без самовыравнивания (рис.8,в).

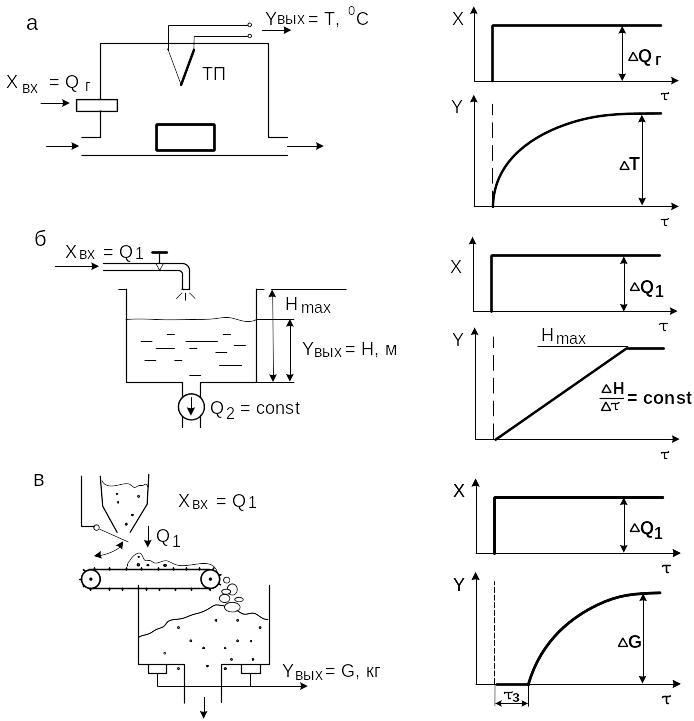
Рис.8 Объекты различного вида и траектории кривых разгона, соответствующих каждому типу объектов

Большинство объектов металлургического производства относится к первой группе. Изменение выходной величины после скачкообразного входного возмущающего воздействия происходит с постоянно уменьшающейся скоростью до момента достижения нового установившегося значения (рис.8,а).

Свойство объекта восстанавливать нарушенное равновесие называется самовыравниванием.

В объектах без самовыравнивания изменение выходной величины происходит с постоянной скоростью и беспредельно (до возникновения аварийных ситуаций) – рис.8,б.

В объектах с запаздыванием регулируемая величина начинает изменяться не одновременно с изменением входной величины, как в предыдущих случаях, а через некоторое время _З, называемое временем запаздывания. Для рис.8,в: _З = L/V_L, где V_L – скорость движения на транспортном участке L.

Реальные кривые разгона (рис.9), полученные на промышленных объектах, отличаются от рассмотренных выше и имеют S-образный вид:

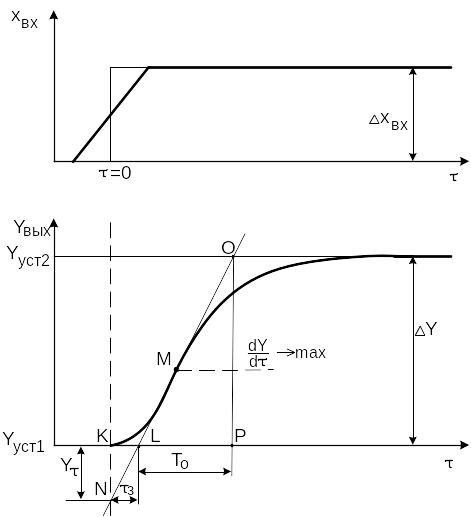
Рис.9 Реальная кривая разгона

Для количественной оценки динамических свойств объектов используются следующие параметры.

_З – время запаздывания – отрезок времени от начала возмущения  = 0 до момента начала изменения выходной величины с постоянной максимальной скоростью или до момента пересечения касательной к Y=f() в точке максимальной скорости с осью времени.

Т_О – время разгона (постоянная времени) – время, в течение которого выходная величина переходит из одного установившегося состояния Y_УСТ1 в другое Y_УСТ2, при условии изменения этой величины с постоянной максимальной скоростью . Время разгона характеризует инерционные свойства объекта.

К_ОБ – коэффициент передачи объекта – число единиц измерения выходной величины, приходящихся на единицу входной величины (см. формулу (1)).

Иногда, особенно для теплоэнергетических объектов, вместо постоянной времени Т_О используют параметр  – скорость разгона, а вместо коэффициента передачи К_ОБ используют коэффициент самовыравнивания – :

(13)

(14)

где Х, Y, Y_ определены графически на рис.9.

Соотношения между  и К_ОБ следующее:

(15)

Соотношение между  и Т_О можно вывести из подобия треугольников KLN и PLO (см. рис.9):

Подставив получившееся выражение в формулу (13), получим:

(16)

В теории автоматического управления вместо кривой разгона используется переходная функция, представляющая собой траекторию изменения выходной величины во времени, вызванном единичным входным ступенчатым воздействием Х = 1 при условии, что до момента приложения этого воздействия система находится в покое.

В большинстве случаев динамические свойства объектов с самовыравниванием можно представить последовательным соединением двух инерционных звеньев первого порядка с постоянными времени Т₁ и Т₂. Структурная схема такого соединения показана на рис.10:

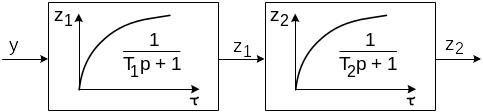
Рис.10 Структурная схема представления динамических свойств ОУ с самовыравниванием

Передаточная функция последовательного соединения двух инерционных звеньев первого порядка имеет вид:

(17)

Для определения параметров Т₁ и Т₂ по экспериментальной кривой разгона в большинстве случаев можно воспользоваться методом Орманса. Последовательность шагов для определения значений Т₁ и Т₂ следующая.

а) Экспериментальная кривая разгона нормируется, т.е. весь диапазон от Y_УСТ1 до Y_УСТ2 (см. рис.9) принимается за единицу и по необходимости начало оси времени смещается вправо на величину транспортного запаздывания – от подачи возмущающего воздействия до начала изменения выходной величины.

б) Из нормированной кривой разгона определяется время, соответствующее значению Y₇ = 0.7 и обозначается как ₇.

в) Полученый интервал делиться на три части, определяется точка _Н = ₇/3. Из точки _Н поднимается перпендикуляр до кривой разгона и определяется величина Y_Н = Y(_Н).

г) Постоянная времени объекта определяется с помощью вспомогательной величины Z*. Для нахождения которой используется номограмма, представленная на рис.11.

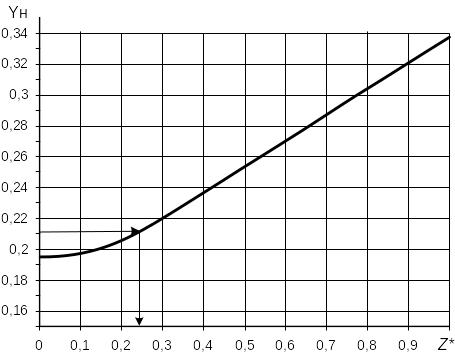
Рис.11 Номограмма для определения величины Z*

д) Величины Т₁ и Т₂ рассчитываются по формулам:

(18)

На рис.12 показаны шаги по определению ₇ и _Н по экспериментальной кривой разгона, изображенной точками. Получили значения: ₇ = 28 с, _Н = 9,3 с и Y_Н = 0,212. В соответствии с номограммой рис.11 определили Z* = 0.24. Сплошной линией показан результат расчета по модели полученной соединением двух инерционных звеньев первого порядка с найденными по методу Орманса (18) постоянными времени Т₁ = 14.5 и Т₂ = 8,9 с.

Решение уравнения при ступенчатом входном сигнале будет иметь вид:

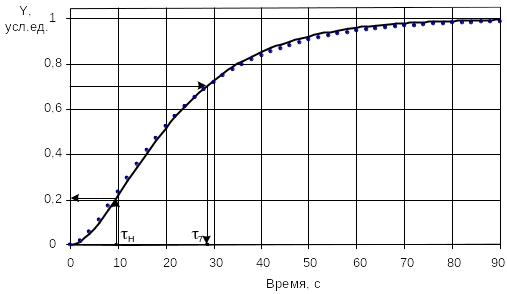
Рисунок 12 – Построение кривой разгона методом Орманса

···· экспериментальная; ––– расчетная кривая разгона

В некоторых случаях, когда значение величины Y_Н оказывается меньше 0.19, воспользоваться номограммой невозможно. Это свидетельствует о том, что объект не может быть с достаточной точностью описан последовательным соединением двух инерционных звеньев. В таком случае следует воспользоваться другими методами. Например, методом наименьших квадратов или, если это допустимо, увеличить время транспортного запаздывания и сместить начало оси времени правее. Если T₁ >>T₂, то можно перейти к модели первого порядка.

Для определения реакции объекта на произвольное входное воздействие решение дифференциального уравнения должно производиться численным методом. Самым распространенным методом решения дифференциального уравнения первого порядка является метод Эйлера.

Основанный на разностном представлении дифференциального уравнения метод Эйлера позволяет решать линейные дифференциальные уравнения первого порядка. Для инерционного звена  порядка с передаточной функцией вида

(19)

дифференциальное уравнение, связывающее вход и выход звена, будет иметь вид:

или

Представим производную в разностном виде:

или

(19)

где Z_i – текущее значение выходного сигнала в момент времени _i ; Z_i-1 – значения сигнала в предыдущий момент времени _i-1; Y_i – текущее входное значение сигнала.

Используя разностное уравнение (19), можно найти траекторию выходного сигнала на любой входной сигнал Y.

Для расчета выходной величины объекта, представленного двумя инерционными звеньями первого порядка, необходимо выходную величину первого звена Z₁ использовать как входную величину для следующего звена.

При расчете выходной величины для первого инерционного звена следует учитывать коэффициент передачи объекта. Входную величину рассчитывают по статической характеристике.

За начальное значение Y, Z₁ и Z₂ необходимо брать установившееся значение до возмущения – Y_УСТ1.

Шаг расчета  необходимо выбирать в 5-10 раз меньший, чем наименьшая постоянная времени в цепочке последовательно соединенных инерционных звеньев.

В таблице 4 приведен пример расчета начального участка кривой разгона ОУ с параметрами:Т₁ = 10,5 с, Т₂ = 9,5 с, Y(X) = 5.2·X_ИМ. Шаг расчета  = 0,1 с при перемещении ИМ с 50% на 60% хода.

Таблица 4

Пример расчета кривой разгона

№		ХИМ	Y=f(XИМ)	Z1	Z2
0	0	50	260	260,00	260,00
1	0.1	60	312	260,50	260,01
2	0.2	60	312	260,99	260,02
3	0.3	60	312	261,47	260,03
4	0.4	60	312	261,95	260,05
5	0.5	60	312	262,43	260,08
..	..	..	..	..	..
..	i = i-1 +	..	Yi =5.2·XИМi	Zi,1 = Zi-1,1 +Zi,1	Zi,2 = Zi-1,2 +Zi,2
..	..	..	..	..	..
..	..	60	312	..	..

Из формулы (19) для рассмотренного в таблице 4 случая: