2.7.2. Трубные пучки

Теплообменные аппараты с одиночно распо­ложенной трубой в поперечном потоке жидкости применяются редко, чаще они компонуются из трубных пучков. По рас­положению труб трубные пучки могут быть коридорными (рис. 2.14, а) и шахматными (рис. 2.14, б).

а б

Риc. 2.14

В них трубы первого ряда находятся приблизи­тельно в тех же условиях, что и одиночный цилиндр. На тепло­обмене второго ряда сказывается турбулизация потока, создаваемая первым рядом, и т.д., но этот эффект постепенно ослабевает по мере увеличения числа предшествующих поперечных рядов. Экспериментально установлено, что начиная с третьего ряда поток практически стабилизируется, поэтому и средний коэффициент теплоотдачи для всех последующих рядов можно считать постоянной вели­чиной. Коэффициент теплоотдачи первого ряда составляет прибли­зительно 60 % от стабилизированных значений коэффициентов теплоотдачи ₃ как для коридорного, так и для шахматного пучков. Для второго ряда в коридорном пучке эта величина составляет 90 %, а при шахматном располо­жении труб – 70% от ₃.

На интенсивность теплообмена пучков влияет также плотность пучка, которую можно характеризовать соотношениями между поперечным шагом s₁, продольным шагом s₂ и диамет­ром труб (рис. 2.12 б, 2.14).

Стабилизированный коэффициент теплоотдачи для многорядных в продольном направлении пучков труб в диапазоне определяется по формулам:

– при коридорном расположении труб

, (2.50)

где ,

– при шахматном расположении труб

, (2.51)

где приипри.

В числа Nu и Re введены в качестве характерного размера наружный диаметр труб d, в качестве характерной скорости – скорость в самом узком поперечном сечении между трубами, а все теплофизические параметры отнесены к средней температуре потока.

Средний коэффициент теплоотдачи к пучку из m труб определяется по формуле

. (2.52)

2.8. Критериальные формулы для описания теплообмена при свободной конвекции

2.8.1. Свободная конвекция в большом объеме

В этом случае предполагается, что жидкая или газообразная среда простирается в бесконечность по нормали к поверхности внесенного в нее твердого тела. При этом выделяют свободную конвекцию у вертикального расположения пластины (плиты, стены) или трубы и свободную конвекцию у горизонтально расположенной трубы.

При термической свободной конвекции у вертикальной поверхности нагретого тела (), начиная от нижней кромки, течение в пограничном слое сначала ламинарно. На некотором расстоянии от нижней кромки толщина ламинарного пограничного слоя становится большой, его устойчивость потока теряется и течение в пограничном слое становится локонообразным. Еще выше оно становится турбулентным (рис. 2.15).

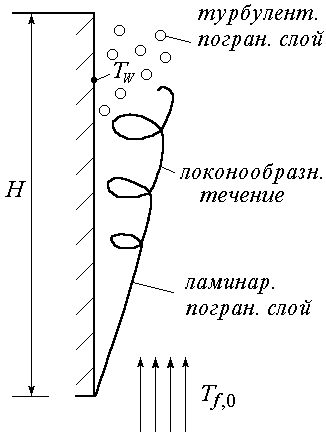
Рис. 2.15

Естественно, что интенсивность теплообмена на выделенном участке плиты зависит от того, какова протяженность находящегося на нем ламинарного, локонообразного или турбулентного течений.

В 2.3 было показано, что критериальные формулы для описания теплообмена при свободной конвекции должны иметь вид связи между числом Нуссельта и критерием Рэлея

(2.53)

Экспериментально установленные зависимости для вертикальной плиты или трубы при постоянной температуре их поверхности T_W=constтаковы:

а) для диапазона 10³<Ra< 10⁹

(2.54)

б) для значений Ra> 10⁹

(2.55)

где и– средние значения числа Нуссельта и коэффициента теплоотдачи на участке высотоюH, отсчитанной от нижней кромки;Ra=gH³(T_W – )Pr/²– критерий Рэлея; – температурный фактор.

Формула (2.55) соответствует случаям больших значений критерия Рэлея, на которые влияет наибольшим образом высота Hплиты (трубы), так как в формулу для расчетаRaвходитH³. При этом практически вся пластина омывается потоком, движущимся свободно в турбулентном режиме, а протяженность участков ламинарного и локонообразного течений пренебрежимо мала.

Нетрудно видеть, что в этом режиме имеет место независимость (автомодельность) величины от протяженностиH, что можно показать, если формулу (2.55) привести к виду

(2.55)

Для горизонтально расположенной трубы в диапазоне 10³<Ra< 10⁸опытные данные приT_W=constаппроксимируются зависимостью

(2.56)

где и– средние значенияNuипо периметру трубы с наружным диаметромd;– критерий Рэлея.

Отметим, что при постоянной плотности теплового потока q_W=constчерез поверхность омываемого тела интенсивность теплоотдачи несколько больше (примерно на 7 %), чем приT_W=const.

В формулах (2.54)–(2.56) теплофизические характеристики среды выбираются по полусумме температур поверхности и омывающей ее среды (T_W+)/2, а разность этих же температурT_W–подставляется по модулю.

Обращаем внимание на то, что получены критериальные зависимости Nu=f(Ra,C_t) и для значенийRa< 10³, которые приводятся в соответствующей литературе.